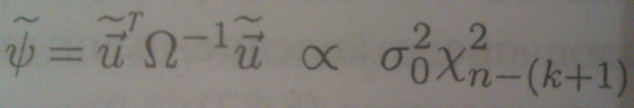Тест Голдфелда–Квандта гомоскедастичности случайных возмущений в схеме Гаусса – Маркова

Тест Голдфелда-Квандта предназначен для проверки предпосылки

Var(u ₁)=Var(u ₂)=…=Var(u_n)= Ϭ ² теоремы Гаусса-Маркова о гомоскедастичности случайного остатка в модели y = a ₀ + a ₁ x ₁ + a ₂ x ₂ +…+ a_kx_k + u                                                                                      (1)

             E(u | x)=0, E(u² | x)= Ϭ_u ²

т.е. для проверки статистической гипотезы о равенстве дисперсий случайных остатков в уравнениях наблюдений y = X a + a:

H₀ : Var(u₁)=Var(u₂)=…=Var(u_n)= Ϭ ²                                               (2)

Неадекватность гипотезы (2) порождает негативные для МНК-оценок

a =f ⃰ (X, y)=f _МНК (X, y)=M(X) y =(X^TX)^-1X^T y

 

  u₁² + u₂² + … + u _n ²

Ϭ_u ² = n – (k + 1)              определённые последствия.

Рассмотрим алгоритм теста (статистической процедуры) Голдфелда-Квандта, а затем проведём его обоснование. Тест Голдфелда-Квандта реализуется в итоге следующих шагов.

Шаг 1. Уравнения наблюдений объекта y = X a + a следует упорядочить по возрастанию суммы модулей значений предопределённых переменных модели (1), т.е. по возрастанию значений

z ₁ = | x _{1 i} | + | x _{1 i} | +…+ | x _{1 i} |                                                                      (3)

Замечание. В этот пункт процедуры Голдфелда-Квандта заложена естественная предпосылка, что возможная гетероскедастичность случайного остатка в модели (1), т.е. зависимость его условий дисперсии Var(u) = E(u ² | x) от объясняющих переменных модели, имеет специальный вид:

E (u ² | x) = f (| x ₁ |+| x ₂ |+…+| x_k |) = f (z),                                                          (4)

Причём функция f (z) является либо возрастающей, либо убывающей. Нужно подчеркнуть, что если случайный остаток гомоскедастичен, то любая зависимость Var(u) = E(u ² | x) от x, а частности зависимость (4), отсутствует. Добавим, что после вычисления в отдельном столбце листа Excel величин (3) упорядочение уравнений наблюдений y = X a + a осуществляется командой «Сортировка по возрастанию» из категории «Данные».

Шаг 2. По первым n ′ упорядоченным уравнениям наблюдений объекта (где n ′ удовлетворяет условиям

k +1 < n ′, n ′ ≈ 0,3 n,                                                                                     (5)

k +1 – количество оцениваемых коэффициентов функции регрессии) вычислить МНК-оценки параметров модели и величину n ′

ESS₁ = ∑ u_i²,                                                                                                      (6)

           i =1

где

u_i = y_i – y_i = y_i – (a ₀ +a ₁ x _{1 i} + … + a_kx_ki) -                                                  (7)

МНК-оценка случайного возмущения u_i.

Замечание. Напомним, что функция ЛИНЕЙН Excel размещает величину ESS в ячейке B n +5, т.е. во втором столбце последней строки выделенного массива.

Шаг 3. По последним n ′ упорядоченным уравнениям наблюдений вычислить МНК-оценку параметров модели и величину ESS, которую обозначим ESS ₂.

Шаг 4. Вычислить статистику

  ESS₁

GQ = ESS ₂                                                                                                     (8)

Шаг 5. Задаться уровнем значимости ɑ и с помощью функции FРАСПОБР Excel при количествах степеней свободы ʋ₁, ʋ₂, где

ʋ₁ = ʋ₂ = n ′ - (k +1),

определить (1- ɑ)-квантиль, F _крит= F _{1- ɑ} распределения Фишера.

Шаг 6. Принять гипотезу (2), если справедливы неравенства

GQ ≤ F _крит                                                                                                                                                                                                                         (9)

GQ ^-1 ≤ F _крит

т.е.               при справедливых неравенствах (9) случайный остаток в модели (1) полагать гомоскедастичным. В противном случае гипотезу (2) отклонить как противоречащую реальным данным и сделать вывод о гетероскедастичности случайного остатка в модели (1).

Замечание. Обсужденный выше тест корректен в ситуации, когда случайные остатки в уравнениях наблюдений y = X a + a распределены по нормальному закону и все другие предпосылки теоремы Гаусса-Маркова справедливы.

Проведём обоснование теста Голдфелда-Квандта. Если вектор случайных остатков в уравнениях наблюдений имеет нормальный закон распределения и все предпосылки теоремы Гаусса-Маркова справедливы, то согласно

величины ESS ₁ и ESS ₂ являются случайными переменными и распределены (с точностью до множителя Ϭ_u ²) по закону хи-квадрат с количеством степеней свободы n ′ -(k +1). Кроме того, согласно предпосылке

Cov(u_i, u_j)=0, i ≠ j

эти переменные независимые. Значит, и статистика (8), и обратная к ней величина GQ ^-1 являются случайной переменной и имеют распределение Фишера с количествами степеней свободы ʋ₁, ʋ₂. Следовательно, критерием гипотезы (2) может служить множество

Z [ H ₁]=(F _{1- ɑ} , +∞).                                                                                   (10)

Если величина GQ (или величина GQ ^-1) попадает в множество (10), то гипотезу (2) следует отклонит ь в пользу альтернативной гипотезы

  H ₁= H ₀,                                                                                                              (11)

Представляющей отрицание гипотезы (2), т.е. означающей гомоскедастичность случайного остатка в модели (1). Второе условие (приближенное равенство) в (5) обеспечивает максимальную мощность критерия (9).