
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование корреляционных зависимостейСтр 1 из 4Следующая ⇒
МАД Лабораторная работа 2 ИССЛЕДОВАНИЕ КОРРЕЛЯЦИОННЫХ ЗАВИСИМОСТЕЙ МЕЖДУ ПРИЗНАКАМИ Цель работы: научиться исследоватькорреляционные зависимости между признаками. Задание для работы в аудитории По предложенным преподавателем исходным данным требуется исследовать влияние некоторых признаков X 1 , X 2, X 3, X 4, X 5. на признак Y. Для выполнения поставленного задания необходимо: 1. Построить графики данных для X 1 , X 2, X 3, X 4, X 5., Y. Оцените визуально наличие или отсутствие грубых погрешностей в каждом признаке. Удалите резко выделяющееся наблюдение признака.
2. Проверить гипотезу о нормальном распределении признаков: Y, X 1 , X 2, X 3, X 4, X 5.. В отчете результаты выполнения представить в виде таблицы: Статистические характеристики исходной информации
При проверке нормальности распределения признаков используйте неравенства (11) и (12) теоретической части описания лабораторной работы. Сделайте выводы.
2. В случае невыполнения предпосылок об однородности и нормальности анализируемых случайных величин необходимо провести корректировку исходного массива данных. В отчете результаты выполнения представить в виде таблицы. Распределение значений признака по диапазонам рассеяния признака относительно
Сделать выводы. Посмотрите, имело ли смысл не удалять из выборочных данных резко выделяющиеся наблюдения признака (п.1). Если это не имело смысла (наблюдение не является резко выделяющимся), верните наблюдение в выборку.
3. Постройте поля корреляции для определения существования и форм зависимости признака Y от признаков X 1 , X 2, X 3, X 4, X 5. В отчете привести поля корреляции. Сделать выводы по каждому полю корреляции.
4. Изучите зависимость признака Y от признаков X 1 , X 2, X 3, X 4, X 5. путем расчета выборочных парных линейных коэффициентов корреляции. В отчете привести формулу расчета выборочных парных линейных коэффициентов корреляции. Результаты расчетов свести в таблицу.
Исследование корреляционной зависимости признака Y от признаков X 1 , X 2, X 3, X 4, X 5.
Сделать выводы.
5. Проверьте значимость каждого выборочного коэффициента корреляции.
В отчете привести теоретическую часть проверки значимости выборочного коэффициента корреляции. Результаты расчетов свести в таблицу. Проверка значимости выборочных коэффициентов корреляции
Сделать выводы.
6. Постройте доверительный интервал для каждого коэффициента корреляции: Результаты расчетов свести в таблицу. Доверительные интервалы выборочных коэффициентов корреляции
Сделать выводы.
7. Построить матрицу парных линейных коэффициентов корреляции и выявить коллинеарные признаки. В отчете привести матрицу парных линейных коэффициентов корреляции, проанализировать ее, сделать выводы. Пример анализа корреляционной матрицы представлен в настоящих методических указаниях.
8. Сделать выводы по каждому пункту и по всей работе в целом с целью определения признаков, которые целесообразно включить в уравнение линейной регрессии. Предложить модели уравнений регрессии.
Индивидуальные задания выполняются по вариантам.
Требования к отбору факторов для корреляционного анализа
Отбор факторов для корреляционного анализа является очень важным моментом. От того, насколько правильно он сделан, зависит точность выводов по итогам анализа. Главная роль при отборе факторов принадлежит теории, а также практическому опыту анализа. При этом необходимо придерживаться следующих правил. 1. При отборе факторов в первую очередь следует учитывать причинно-следственные связи между показателями, так как только они раскрывают сущность изучаемых явлений. Анализ же таких факторов, которые находятся только в математических соотношениях с результативным показателем, не имеет практического смысла. 2. При создании многофакторной корреляционной модели необходимо отбирать самые значимые факторы, которые оказывают решающее воздействие на результативный показатель, так как охватить все условия и обстоятельства практически невозможно. Факторы, которые имеют критерий надежности по Стьюденту меньше табличного, не рекомендуется принимать в расчет. 3. Все факторы должны быть количественно измеримы, т.е. иметь единицу измерения. 4. В корреляционную модель линейного типа не рекомендуется включать факторы, связь которых с результативным показателем имеет криволинейный характер. 5. Не рекомендуется включать в корреляционную модель взаимосвязанные факторы. Если парный коэффициент корреляции между двумя факторами больше 0,85, то по правилам корреляционного анализа один из них необходимо исключить, иначе это приведет к искажению результатов анализа. 6. Нежелательно включать в корреляционную модель факторы, связь которых с результативным показателем носит функциональный характер. Большую помощь при отборе факторов для корреляционной модели оказывают аналитические группировки, способ сопоставления параллельных и динамических рядов, линейные графики. Благодаря им можно определить наличие, направление и форму зависимости между изучаемыми показателями. Отбор факторов можно производить также в процессе решения задачи корреляционного анализа на основе оценки их значимости по критерию Стьюдента, о котором будет сказано ниже. Поскольку корреляционная связь с достаточной выразительностью и полнотой проявляется только в массе наблюдений, объем выборки данных должен быть достаточно большим, так как только в массе наблюдений сглаживается влияние других факторов. Чем большая совокупность объектов исследуется, тем точнее результаты анализа. По коэффициенту вариации. Если коэффициент вариации превышает 33%, говорить о нормальности распределения данных выборки нельзя. Предварительный анализ с помощью коэффициента вариации дает самую грубую оценку.
2. По коэффициентам эксцесса и асимметрии (получаются неплохие результаты при большом числе наблюдений (n > 100) и использовании выборочных коэффициентов эксцесса и асимметрии). Для нормально распределенной случайной величины коэффициенты эксцесса и асимметрии равны 0. Поэтому, если соответствующие эмпирические величины достаточно малы, можно предположить, что генеральная совокупность распределена по нормальному закону.
. Принято говорить, что предположение о нормальности распределения не противоречит имеющимся данным, если асимметрия лежит в диапазоне от -0,2 до 0,2, а эксцесс – от -1 до 1.
В практических расчетах в качестве асимметрии применяется нормированный коэффициент асимметрии третьего порядка, который не зависит от масштаба, выбранного при измерении варианта, так как является отвлеченной величиной:
Если Для определения крутизны (заостренности) распределения вычисляется центральный момент четвертого порядка и определяется нормированный момент четвертого порядка:
Для нормального распределения
При симметричном распределении Однако случай, когда если где то асимметрия считается несущественной, а ее наличие объясняется воздействием случайных факторов. В противном случае асимметрия статистически значима (существенна) и факт ее наличия требует дополнительной интерпретации.
Аналогично, если
где то эксцесс считается незначительным и его величиной можно пренебречь. 3. На основе среднего абсолютного отклонения. Для не очень больших выборок (n <120) можно вычислить среднее абсолютное отклонение (САО):
где n – объем выборки;
Для выборки, имеющей приближенно нормальный закон распределения, должно выполняться условие:
4. На основе критериев согласия (например, χ2 (хи-квадрат)). При малом n (50< n < 100) наиболее убедительные результаты дает использование критериев согласия. Здесь нулевая гипотеза Н0 представляет собой утверждение о том, что распределение генеральной совокупности, из которой получена выборка, не отличается от нормального. Один из критериев - непараметрический критерий χ2 (хи-квадрат). Он основан на сравнении эмпирических частот интервалов группировки с теоретическими (ожидаемыми) частотами, рассчитанными по формулам нормального распределения. Для его применения желательно иметь не менее 40 – 50 выборочных данных, сгруппированных не менее чем в 7 интервалов, в каждом из которых находится хотя бы 5 наблюдений.
5. На основе размаха варьирования. Проверку гипотезы нормальности распределения для сравнительно широкого класса выборок (3< n <1000) можно выполнить с помощью метода, основанного на размахе варьирования R. Для его использования определяют размах упорядоченной совокупности наблюдений (
Если фактическое численное значение Анализ В случае невыполнения предпосылок об однородности и нормальности анализируемых случайных величин необходимо провести корректировку исходного массива данных. С этой целью можно воспользоваться «правилом трех сигм». Для каждой случайной величины формируется таблица 2.5
Таблица 2.5 - Распределение значений признака по диапазонам рассеяния признака относительно
На основе данных таблицы 2.5 структура рассеяния значений признака по трем диапазонам сопоставляется со структурой рассеяния по правилу «трех сигм», справедливому для нормальных и близких к нему распределений:
68,3% значений располагаются в диапазоне ( 95,4% значений располагаются в диапазоне ( 99,7% значений располагаются в диапазоне ( Если полученная в табл. 2.5 структура рассеяния хi по 3-м диапазонам незначительно расходится с правилом «трех сигм», можно предположить, что распределение единиц совокупности по данному признаку близко к нормальному. Расхождение с правилом «трех сигм» может быть существенным. Например, менее 60% значений хi попадают в центральный диапазон ( Если исходные данные неоднородные или не распределены нормально, то их корректируют. Из массива первичной информации исключаются все резко выделяющиеся (аномальные) значения, т.е. значения, уровень которых не попадает в интервал Пример отсева грубых погрешностей методом максимального относительного отклонения: Пирометром измеряется температура поверхности нагретого тела. Будем предполагать, что температура видимой поверхности нагретого тела во всех точках одинакова. Различными исследователями было проведено шесть измерений температуры и получены следующие их значения: Температура, 0С: 925, 950, 975, 1000, 1025, 1050 (n=6). Имеются ли среди этих измерений грубые погрешности? Предварительно вычислим оценки
Для определения Sx использовали (n-1), т.к. истинное значение измеряемой температуры нам не известно. Заметим, что здесь это важно, т.к. сделано мало измерений (всего n=6). Выберем измерения, имеющие наибольшее отклонение от среднеарифметического значения. Таких значений оказалось два: 925 0C и 1050 0C. Для оценки нуль-гипотезы о несущественности отклонения выбранного Если tэксп>ta, Вычислим
При a=0,05 и Так как tэксп<ta, Аналогично проводим расчеты для второго значения - 925 0C:
Так как tэксп<ta, В результате сформирован новый массив данных, который используется в дальнейшем анализе. Однако для этого массива тоже предварительно рассчитываются основные характеристики.
Другой способ отсева грубых погрешностей – на основе размаха варьирования. Для этого определяют размах упорядоченной совокупности наблюдений (
Если какой-либо член вариационного ряда, например
где z – критериальное значение. Нулевую гипотезу (об отсутствии грубой погрешности) принимают, если указанное неравенство выполняется. Если Коэффициент z зависит от числа членов вариационного ряда n, что представлено в таблице 2.6. Таблица 2.6 – Критерий вариационного размаха
Пример По 25 территориям страны изучается влияние климатических условий на урожайность зерновых у (ц/га). Для этого были отобраны две объясняющие переменные: х1 – количество осадков в период вегетации (мм), х2 – средняя температура воздуха (град. С). Построена матрица парных коэффициентов корреляции (табл. 1.5).
Таблица 2.6 – Матрица парных линейных коэффициентов корреляции
Поясните смысл приведенных коэффициентов. Какое уравнение лучше строить: 1) парную регрессию у на х1; 2) парную регрессию у на х2; 3) множественную регрессию? Решение 1. В клетках матрицы находятся парные линейные коэффициенты корреляции. Они оценивают степень линейной связи между двумя признаками. 2. Анализ первого столбца матрицы парных коэффициентов корреляции. По матрице можно сделать вывод о сильной положительной связи между признаками у и х1 и об умеренной отрицательной связи между признаками у и х2. В данном случае целесообразным является построение парной регрессии у на х1 и множественной регрессии. Выбор между ними будет основываться на величине коэффициента детерминации регрессионной модели. 3. Анализ всех остальных элементов матрицы (кроме элементов первого столбца). Между признаками х1 и х2 мультиколлинеарности не наблюдается, так как парный линейный коэффициент корреляции между этими признаками равен -0,3 (слабая связь). Поэтому выводы п.2 остаются в силе. Вопросы к защите лабораторной работы №2 1. Сформулируйте понятия функциональной и стохастической зависимостей. 2. Какая взаимосвязь случайных величин называется корреляционной? 3. Перечислите требования к отбору исходных факторов для изучения корреляционной зависимости между ними. 4. Поясните требование однородности исходных данных. 5. Поясните, что представляет собой коэффициент вариации и как он рассчитывается? 6. Что представляет собой дифференциальная функция нормального распределения? 7. Назовите основные свойства нормального распределения. 8. Назовите варианты проверки гипотезы о нормальном распределении исходных данных. 9. Поясните, каким образом проверяется гипотеза о нормальном распределении случайной величины на основе коэффициентов асимметрии и эксцесса? 10. Поясните, каким образом проверяется гипотеза о нормальном распределении случайной величины на основе критерия χ2 (хи-квадрат). 11. Поясните, в чем заключается правило «трех сигм»? Каким образом его используют в практических исследованиях? 12. В каких случаях требуется корректировка исходной информации, предполагаемой для использования в корреляционном анализе? 13. Каким образом осуществляют корректировку исходной информации, используя правило «трех сигм»? 14. Каким образом можно осуществить отсев грубых погрешностей методом максимального относительного отклонения? 15. Каким образом можно осуществить отсев грубых погрешностей с использованием размаха вариации? 16. В чем заключается основная задача корреляционного анализа? 17. Для оценки какой корреляционной зависимости используется выборочный коэффициент корреляции? Каковы его свойства? 18. Что такое «поле корреляции»? Каким образом оно анализируется? 19. Как проверяется значимость коэффициента корреляции? 20. Поясните, что представляет собой матрица парных линейных коэффициентов корреляции? 21. Для совокупности трех случайных величин X, Y, Z получена матрица выборочных коэффициентов корреляции 22. Каким образом выявляются мультиколлинеарные признаки? 23. Что оценивает выборочный коэффициент множественной корреляции? 24. Поясните практическое использование матрицы парных линейных коэффициентов корреляции. ПРИЛОЖЕНИЯ Критические значения критерия Стьюдента при уровне значимости 0,10, 0,05, 0,01
МАД Лабораторная работа 2 ИССЛЕДОВАНИЕ КОРРЕЛЯЦИОННЫХ ЗАВИСИМОСТЕЙ МЕЖДУ ПРИЗНАКАМИ Цель работы: научиться исследоватькорреляционные зависимости между признаками. Задание для работы в аудитории По предложенным преподавателем исходным данным требуется исследовать влияние некоторых признаков X 1 , X 2, X 3, X 4, X 5. на признак Y. Для выполнения поставленного задания необходимо: 1. Построить графики данных для X 1 , X 2, X 3, X 4, X 5., Y. Оцените визуально наличие или отсутствие грубых погрешностей в каждом признаке. Удалите резко выделяющееся наблюдение признака.
2. Проверить гипотезу о нормальном распределении признаков: Y, X 1 , X 2, X 3, X 4, X 5.. В отчете результаты выполнения представить в виде таблицы: Статистические характеристики исходной информации
При проверке нормальности распределения признаков используйте неравенства (11) и (12) теоретической части описания лабораторной работы. Сделайте выводы.
2. В случае невыполнения предпосылок об однородности и нормальности анализируемых случайных величин необходимо провести корректировку исходного массива данных. В отчете результаты выполнения представить в виде таблицы. Распределение значений признака по диапазонам рассеяния признака относительно
Сделать выводы. Посмотрите, имело ли смысл не удалять из выборочных данных резко выделяющиеся наблюдения признака (п.1). Если это не имело смысла (наблюдение не является резко выделяющимся), верните наблюдение в выборку.
3. Постройте поля корреляции для определения существования и форм зависимости признака Y от признаков X 1 , X 2, X 3, X 4, X 5. В отчете привести поля корреляции. Сделать выводы по каждому полю корреляции.
4. Изучите зависимость признака Y от признаков X 1 , X 2, X 3, X 4, X 5. путем расчета выборочных парных линейных коэффициентов корреляции. В отчете привести формулу расчета выборочных парных линейных коэффициентов корреляции. Результаты расчетов свести в таблицу.
Исследование корреляционной зависимости признака Y от признаков X 1 , X 2, X 3, X 4, X 5.
Сделать выводы.
5. Проверьте значимость каждого выборочного коэффициента корреляции.
В отчете привести теоретическую часть проверки значимости выборочного коэффициента корреляции. Результаты расчетов свести в таблицу. Проверка значимости выборочных коэффициентов корреляции
Сделать выводы.
6. Постройте доверительный интервал для каждого коэффициента корреляции: Результаты расчетов свести в таблицу. Доверительные интервалы выборочных коэффициентов корреляции
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-10; просмотров: 132; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.45.162 (0.21 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

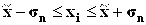
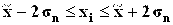

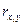
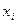 и y
и y

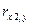

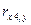
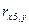
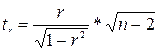
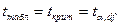
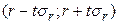 .
.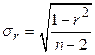
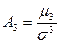 . (8)
. (8)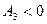 , то в ряду распределения преобладают варианты, которые меньше, чем средняя, т.е. ряд отрицательно асимметричен (или с левосторонней скошенностью – более длинная ветвь влево). Если
, то в ряду распределения преобладают варианты, которые меньше, чем средняя, т.е. ряд отрицательно асимметричен (или с левосторонней скошенностью – более длинная ветвь влево). Если 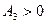 , то для ряда распределения характерна положительная асимметрия (правосторонняя скошенность – более длинная ветвь вправо),
, то для ряда распределения характерна положительная асимметрия (правосторонняя скошенность – более длинная ветвь вправо), 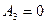 при симметричном распределении, так как варианты равноудалены от
при симметричном распределении, так как варианты равноудалены от 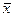 и имеют одинаковую частоту. Поэтому
и имеют одинаковую частоту. Поэтому 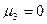 .
.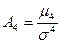 . (9)
. (9)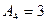 . При оценке крутизны в качестве эталонного выбирается нормальное распределение, которое сравнивается с фактическим и вычисляется показатель эксцесса распределения:
. При оценке крутизны в качестве эталонного выбирается нормальное распределение, которое сравнивается с фактическим и вычисляется показатель эксцесса распределения: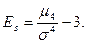 (10)
(10)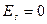 . Если
. Если 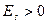 , то распределение является островершинным, если
, то распределение является островершинным, если 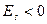 - плосковершинным. В результате более при сравнении распределений двух случайных величин при равенстве их средних предпочтительной является величина с большим коэффициентом эксцесса.
- плосковершинным. В результате более при сравнении распределений двух случайных величин при равенстве их средних предпочтительной является величина с большим коэффициентом эксцесса.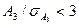 , (11)
, (11)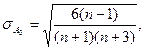 (n – число значений случайной величины),
(n – число значений случайной величины),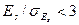 , (12)
, (12)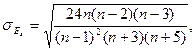
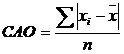
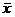 - среднее значение выборки.
- среднее значение выборки.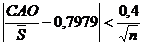 .
. ):
):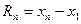 .
. критерия попадает в диапазон табличных значений: для n=10
критерия попадает в диапазон табличных значений: для n=10 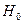 о ненормальном распределении случайной величины отвергается и принимается альтернативная гипотеза
о ненормальном распределении случайной величины отвергается и принимается альтернативная гипотеза 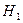 о нормальном распределении случайной величины.
о нормальном распределении случайной величины.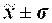 ),
),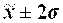 ),
),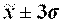 ).
).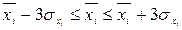 или используют правила отсева грубых погрешностей. Данный критерий надежен при числе измерений n ≥ 20...50. Это правило обычно считается чересчур жестким, в связи с этим рекомендуется назначать границу цензурирования исходя из объёма выборки: при 6 < n ≤1000 она равна 4 «сигма»; при 100 < n ≤1000 − 4,5 «сигма»; при 1000 < n ≤10000 − 5 «сигма». Данное правило используется только при нормальном распределении.
или используют правила отсева грубых погрешностей. Данный критерий надежен при числе измерений n ≥ 20...50. Это правило обычно считается чересчур жестким, в связи с этим рекомендуется назначать границу цензурирования исходя из объёма выборки: при 6 < n ≤1000 она равна 4 «сигма»; при 100 < n ≤1000 − 4,5 «сигма»; при 1000 < n ≤10000 − 5 «сигма». Данное правило используется только при нормальном распределении.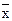 и S:
и S: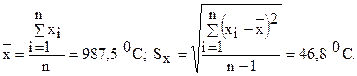
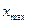 от
от 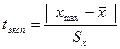 . При этом предполагается, что случайная величина
. При этом предполагается, что случайная величина 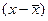 распределена по нормальному закону. Максимальное относительное отклонение сравнивается с теоретическим значением критерия Стьюдента t, которое зависит от уровня значимости α (0,05; 0,1; 0,01) и числа степеней свободы
распределена по нормальному закону. Максимальное относительное отклонение сравнивается с теоретическим значением критерия Стьюдента t, которое зависит от уровня значимости α (0,05; 0,1; 0,01) и числа степеней свободы 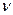 =n-1.
=n-1.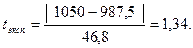

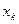 , резко отличается от всех других, то производят проверку, используя следующее соотношение:
, резко отличается от всех других, то производят проверку, используя следующее соотношение: .
. – выборочное среднее арифметическое значение, вычисленное после исключения предполагаемого промаха;
– выборочное среднее арифметическое значение, вычисленное после исключения предполагаемого промаха;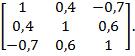 Укажите наиболее тесно связанные пары величины.
Укажите наиболее тесно связанные пары величины.


