
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка гипотез о наличии линейной корреляционной связи ⇐ ПредыдущаяСтр 4 из 4
Для проверки гипотезы о наличии линейной корреляционной связи наибольшее распространение имеет коэффициент линейной корреляции (Пирсона), предполагающий нормальный закон распределения наблюдений. Для двумерной нормально распределенной случайной величины XY при отсутствии линейной корреляции между X и Y коэффициент корреляции равен нулю. Поэтому процедура проверки заключается в расчете выборочной оценке коэффициента корреляции и оценке значимости его отличия от нуля. Коэффициент корреляции – параметр, характеризующий степень линейной взаимосвязи между двумя выборками, рассчитывается по формуле:
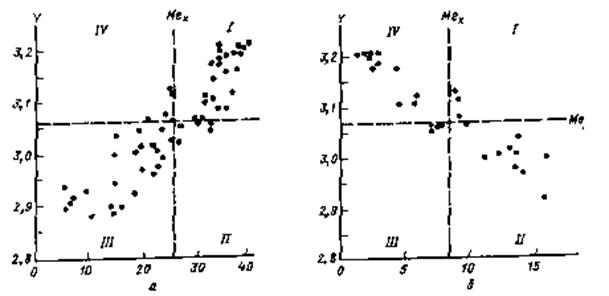
Коэффициент корреляции изменяется от –1 (строгая обратная линейная зависимость) до 1 (строгая прямая пропорциональная зависимость). При значении 0 линейной зависимости между двумя выборками нет. Под прямой зависимостью понимают зависимость, при которой увеличение или уменьшение значения одного признака ведет, соответственно, к увеличению или уменьшению второго. При обратной зависимости увеличение одного признака приводит к уменьшению второго и наоборот. На практике коэффициент корреляции принимает некоторые промежуточные значения между 1 и –1. Для оценки степени взаимосвязи можно руководствоваться следующей классификацией корреляционных связей по абсолютной величине коэффициента корреляции: - очень сильная, практически линейная зависимость между параметрами при r>0,90; - сильная (тесная) при коэффициенте корреляции r>0,7; - умеренная при 0,50<r<0,70; - слабая при 0,30<r<0,5; - практически отсутствуетпри r<0,30. В этих случаях обычно считают, что линейную взаимосвязь между параметрами выявить не удалось. Приближенная оценка коэффициента корреляции может быть получена графическим способом с помощью поля корреляции. Поле точек разделяется на четыре квадранта линиями, соответствующими медианам величин Х и Y. Для оценки коэффициента корреляции используется формула
где n1 – число точек в квадрантах I, III а n2 – в квадрантах II, IV:
Рисунок 1.1 - Поля корреляции прямо и обратно коррелирующих величин
В Excel для вычисления выборочных парных коэффициентов линейной корреляции используется специальная функция КОРРЕЛ (массив1;массив2), где массив1 – это диапазон ячеек со значениями первой случайной величины - первого параметра, массив2 – это второй интервал ячеек со значениями второго параметра (измеренного у тех же объектов, что и первый).
Также возможно использование процедуры «Корреляция» (Сервис - Анализ данных), которая позволяет получить корреляционную матрицу, содержащую коэффициенты корреляции между различными параметрами. Вычислив выборочный коэффициент корреляции, необходимо оценить его статистическую значимость. Не исключено, что ненулевое значение коэффициента является не отражением действительной связи между признаками, а получено в результате специфики данной выборки. Статистическая значимость выборочного коэффициента корреляции проверяется с помощью t -критерия Стьюдента. Фактическое значение t -критерия Стьюдента определяется по формуле:
где n – объем выборочной совокупности, r – выборочный коэффициент корреляции. Фактическое значение t -критерия Стьюдента сравнивается с его табличным значением, которое находят по таблицам Стьюдента с учетом заданного уровня значимости α (α может быть равным 0,5, 0,05 или 0,01) и числом степеней свободы df = n -2. Если
Для того, чтобы понять, насколько значимо отличие выборочного коэффициента корреляции от 0, строят доверительный интервал
Средняя ошибка коэффициента корреляции вычисляется по формуле:
Если 0 не попадает в доверительный интервал, то коэффициент корреляции можно считать статистически значимым. Рассмотренная формула рекомендована к применению при большом числе наблюдений и если r не близка к +1 или -1. В противном случае распределение оценок выборочного коэффициента корреляции отличается от нормального. Чтобы обойти это затруднение Р. Фишером было предложено для оценки существенности r ввести вспомогательную величину z:
При изменении r от -1 до +1 величина z изменяется от - ∞ до + ∞, что соответствует нормальному закону распределения. Стандартная ошибка величины z определяется по формуле:
Далее выдвигается гипотеза Н0 о том, что корреляция отсутствует, т.е. теоретическое значение коэффициента корреляции равно 0. Коэффициент корреляции значимо отличается от нуля, если
Пример По 25 территориям страны изучается влияние климатических условий на урожайность зерновых у (ц/га). Для этого были отобраны две объясняющие переменные: х1 – количество осадков в период вегетации (мм), х2 – средняя температура воздуха (град. С). Построена матрица парных коэффициентов корреляции (табл. 1.5).
Таблица 2.6 – Матрица парных линейных коэффициентов корреляции
Поясните смысл приведенных коэффициентов. Какое уравнение лучше строить: 1) парную регрессию у на х1; 2) парную регрессию у на х2; 3) множественную регрессию? Решение 1. В клетках матрицы находятся парные линейные коэффициенты корреляции. Они оценивают степень линейной связи между двумя признаками. 2. Анализ первого столбца матрицы парных коэффициентов корреляции. По матрице можно сделать вывод о сильной положительной связи между признаками у и х1 и об умеренной отрицательной связи между признаками у и х2. В данном случае целесообразным является построение парной регрессии у на х1 и множественной регрессии. Выбор между ними будет основываться на величине коэффициента детерминации регрессионной модели. 3. Анализ всех остальных элементов матрицы (кроме элементов первого столбца). Между признаками х1 и х2 мультиколлинеарности не наблюдается, так как парный линейный коэффициент корреляции между этими признаками равен -0,3 (слабая связь). Поэтому выводы п.2 остаются в силе. Вопросы к защите лабораторной работы №2 1. Сформулируйте понятия функциональной и стохастической зависимостей. 2. Какая взаимосвязь случайных величин называется корреляционной? 3. Перечислите требования к отбору исходных факторов для изучения корреляционной зависимости между ними. 4. Поясните требование однородности исходных данных. 5. Поясните, что представляет собой коэффициент вариации и как он рассчитывается? 6. Что представляет собой дифференциальная функция нормального распределения? 7. Назовите основные свойства нормального распределения. 8. Назовите варианты проверки гипотезы о нормальном распределении исходных данных. 9. Поясните, каким образом проверяется гипотеза о нормальном распределении случайной величины на основе коэффициентов асимметрии и эксцесса? 10. Поясните, каким образом проверяется гипотеза о нормальном распределении случайной величины на основе критерия χ2 (хи-квадрат).
11. Поясните, в чем заключается правило «трех сигм»? Каким образом его используют в практических исследованиях? 12. В каких случаях требуется корректировка исходной информации, предполагаемой для использования в корреляционном анализе? 13. Каким образом осуществляют корректировку исходной информации, используя правило «трех сигм»? 14. Каким образом можно осуществить отсев грубых погрешностей методом максимального относительного отклонения? 15. Каким образом можно осуществить отсев грубых погрешностей с использованием размаха вариации? 16. В чем заключается основная задача корреляционного анализа? 17. Для оценки какой корреляционной зависимости используется выборочный коэффициент корреляции? Каковы его свойства? 18. Что такое «поле корреляции»? Каким образом оно анализируется? 19. Как проверяется значимость коэффициента корреляции? 20. Поясните, что представляет собой матрица парных линейных коэффициентов корреляции? 21. Для совокупности трех случайных величин X, Y, Z получена матрица выборочных коэффициентов корреляции 22. Каким образом выявляются мультиколлинеарные признаки? 23. Что оценивает выборочный коэффициент множественной корреляции? 24. Поясните практическое использование матрицы парных линейных коэффициентов корреляции.
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-10; просмотров: 772; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.147.87 (0.021 с.) |
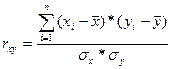 .
.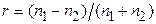 ,
,

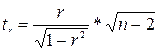 , (1)
, (1)
 , то это означает, что выборочный коэффициент корреляции значим, т.е. он значимо отличается от нуля.
, то это означает, что выборочный коэффициент корреляции значим, т.е. он значимо отличается от нуля.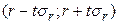 , где t - коэффициент доверия,
, где t - коэффициент доверия, 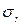 - средняя ошибка коэффициента корреляции. Коэффициент доверия t для доверительной вероятности 0,95 равен 2, для 0,999 равен 3. Доверительная вероятность р=1- α. Таким образом, для р=0,95 α=0,05, для р=0,999 α=0,001.
- средняя ошибка коэффициента корреляции. Коэффициент доверия t для доверительной вероятности 0,95 равен 2, для 0,999 равен 3. Доверительная вероятность р=1- α. Таким образом, для р=0,95 α=0,05, для р=0,999 α=0,001.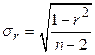 . (2)
. (2)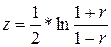 . (3)
. (3)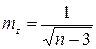 . (4)
. (4) , т.е. если фактическое значение
, т.е. если фактическое значение 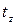 превышает его табличное значение на уровне значимости α.
превышает его табличное значение на уровне значимости α.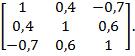 Укажите наиболее тесно связанные пары величины.
Укажите наиболее тесно связанные пары величины.


