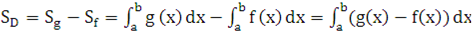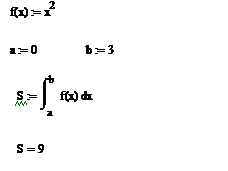Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первое свойство определенного интегралаСодержание книги Поиск на нашем сайте
Константу можно выносить за знак определенного интеграла
Данное свойство можно пояснить на примере вычисления в системе Mathcad определённого интеграла, например, от степенной функции
Демонстрация первого свойства определённого интеграла. Обратите внимание в этом примере, что результат нахождения определённого интеграла можно записать в переменную и в дальнейшем применять её для расчётов.
Второе свойство определенного интеграла
Интеграл от суммы (разности) функций равен сумме (разности) интегралов.
Демонстрация второго свойства определённого интеграла. Если обращать внимание на синтаксис записи определённого интеграла в системе Mathcad, то также справедлива следующая запись.
Демонстрация второго свойства определённого интеграла.
Третье свойство определенного интеграла
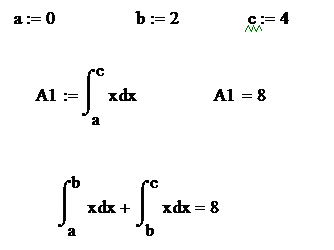
Если f (x) интегрируема по отрезку [a, b] и точка c принадлежит этому отрезку, то В системе Mathcad это может выглядеть следующим образом.
Демонстрация третьего свойства определённого интеграла. Помимо демонстрации третьего свойства определённого интеграла, здесь также можно обратить внимание на то, что сами пределы интегрирования могут задаваться непосредственно через переменную, которая была определена выше или значение которой было получено как результат вычисления каких-либо выражений.
Четвертое свойство определенного интеграла
Смена знака равносильна смене пределов интегрирования
Докажем это при помощи системы Mathcad.
Демонстрация четвёртого свойства определённого интеграла. После того как были даны основные определения определённого интеграла, а также разобраны примеры о том, как работает с определёнными интегралами система Mathcad, перейдём непосредственно к приложению определённого интеграла.
4.
Теория
Один из ярких примеров применения определённого интеграла, следующий из определения, которое было дано выше, - это вычисление площадей фигур. Это приложение относится к геометрическому смыслу определённого интеграла. Вспомним теорию. Пусть f (x) и g(x) - две непрерывные функции, заданные на отрезке [a; b], причём f (x) Если обе функции неотрицательны, то есть f (x)
4.2 Примеры нахождения площади под кривой в системе Mathcad
Для степенной функции.
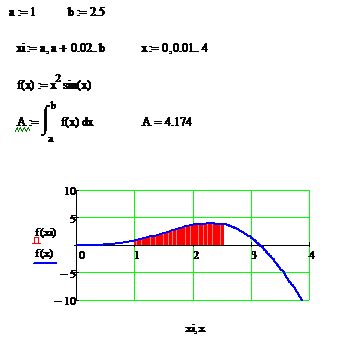
Вычисление площади под кривой при помощи определённого интеграла. Однако для того, чтобы процедура вычисления определённого интеграла была более наглядна, т.е. чтобы можно было визуально увидеть ту площадь, которая вычисляется, Mathcad предоставляет такую возможность визуализации. Смотрите пример ниже.
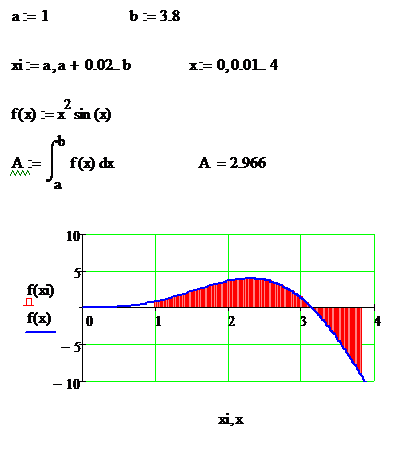
Визуализация геометрической трактовки определённого интеграла. Заштрихованная площадь соответствует той площади, которую вычисляет определённый интеграл. Другими словами, заштрихованная площадь на приведённом выше рисунке равна A = 4,174. Этот пример наглядно показывает, какую площадь и между какими интервалами вычисляет определённый интеграл. В данном случае пределами, как интегрирования, так и пределами для построения площади являются числа a и b. При изменении их значения буде меняться пределы интегрирования, а также будет меняться заштрихованная область на рисунке. Теперь давайте вспомнить из курса математики, что если график функции находится выше оси Ox, т.е. функция на всем промежутке интегрирования принимает положительные значения, то интеграл получается положительным. Если же график функции располагается ниже оси Ox, т.е. функция на всем промежутке интегрирования принимает отрицательные значения, то интеграл получится отрицательным. Если на всем промежутке интегрирования функция принимает как положительные, так и отрицательные значения, то числовое значение определённого интеграла будет складываться из «положительной» части интеграла и его «отрицательной» части. Наглядно это может демонстрировать следующий пример. Сравните его с предыдущим.
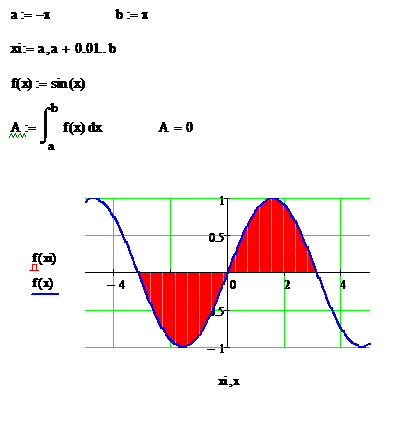
Визуализация геометрической трактовки определённого интеграла. В данном случае при изменении пределов интегрирования меняется и значение этого интеграла. Несмотря на то, что заштрихованная площадь стала больше, само значение интеграла стало меньше, чем в предыдущем примере. Может получиться и так, что значение определённого интеграла будет нулевым. Такое обычно происходит, когда функция периодическая и пределы интегрирования для неё заданы симметрично.
Пример интегрирования тригонометрической функции.
|
||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 229; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

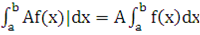 .
.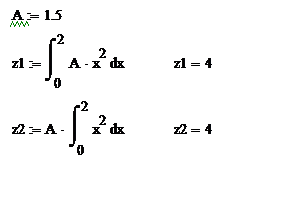
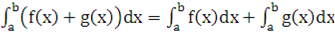
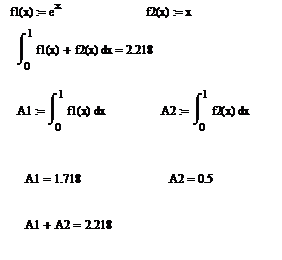
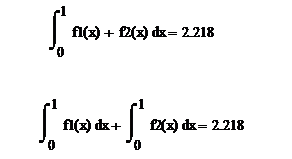
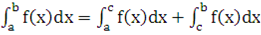
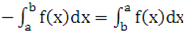
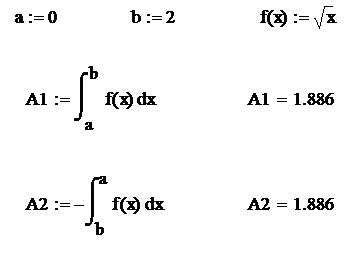
 g(x) при всех x
g(x) при всех x  [a; b]. Между графиками y = f (x) и y = g(x) лежит область D, с боков ограниченная отрезками прямых x = a и x = b.
[a; b]. Между графиками y = f (x) и y = g(x) лежит область D, с боков ограниченная отрезками прямых x = a и x = b.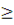 0, то для вычисления площади области D достаточно заметить, что она равна разности площадей областей
0, то для вычисления площади области D достаточно заметить, что она равна разности площадей областей 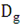 и
и 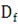 , лежащих между отрезком [a; b] (снизу) и, соответственно, графиком y = g(x) и y = f (x) (сверху). Для нахождения площадей областей
, лежащих между отрезком [a; b] (снизу) и, соответственно, графиком y = g(x) и y = f (x) (сверху). Для нахождения площадей областей