Пространственная решетка. Понятие об элементарной ячейке

Металлы относятся к природным веществам, способным, как было отмечено, иметь в твердом состоянии кристаллическое строение. Особенность подобного строения заключается в том, что материальные частицы твердого тела (атомы, ионы) имеют правильное, закономерное расположение, которое повторяется с определенной периодичностью. Такому упорядоченному размещению атомов в кристалле соответствует периодическое расположение узлов, т.е. геометрических элементов в виде точек. При этом узлы не- обязательно должны совпадать с материальными частицами, поскольку в реальных кристаллах атомы могут размещаться и вне узлов.

Такое упорядочение всегда можно описать, многократно повторяя в пространстве одну и ту же структурную комбинацию, состоящую из малого числа узлов. Указанный комплекс принято называть элементарной ячейкой. В случае двухмерного измерения элементарная ячейка будет представлять собой плоский атомный узор в виде параллелограмма, в трехмерном пространстве она будет изображаться параллелепипедом (рис.3).

В результате весь кристалл можно составить, подгоняя друг к другу                            такие идентичные блоки - элементарные ячейки. Подобное построение приведет к формированию плоской сетки (в двух измерениях) или пространственной решетки (в трех измерениях). Тем самым пространственная решетка (плоская сетка) представляет собой некую бесконечную геометрическую конструкцию, позволяющую воспроизвести особенности периодического повторения в расположении точек (материальных частиц). И главная особенность такого построения - каждая точка имеет окружение, идентичное окружению всех остальных точек.

Таким образом, элементарную ячейку можно определить как наименьший комплекс узлов, многократное повторение которого воспроизводит плоскую сетку или пространственную решетку. Поскольку материальные объекты - металлы - имеют объемную форму, то в дальнейшем элементарную ячейку будем представлять в виде элементарного параллелепипеда. Вершины такой геометрической фигуры как раз и представляются узлами. Обычно их связывают с положениями центров атомов кристалла. При этом не все атомы попадают в вершины ячейки - некоторые могут находиться на ее гранях, другие же размещаются внутри объема. Отметим, что вершинные узлы принадлежат каждой ячейке лишь на 1/8 часть, находящиеся в центре грани - наполовину и только расположенные внутри ячейки относятся к ней целиком.

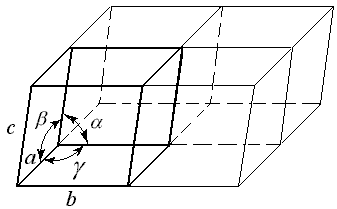
Элементарная ячейка содержит исчерпывающую информацию о характере объемного расположения узлов (сколько их и как они размещаются относительно друг друга в пространстве). Поэтому для описания пространственной решетки вполне достаточно ограничиться рассмотрением элементарной ячейки. При этом геометрическую форму элементарной ячейки можно задать, используя следующие показатели (рис.3):

- углы между ребрами a, b, g, которые называются осевыми или координатными углами;

- длины ребер a, b, c, которые характеризуют наименьшие расстояния между узлами вдоль координатных осей x, y, z и называются параметрами или периодами решетки.

Набор этих показателей принято называть метрикой.

 

 

Рис. 3. Пространственная решетка и ее элементарная ячейка

 

 

     

Различаются простые (примитивные) и сложные элементарные ячейки. Простой называется такая ячейка, внутри которой нет узлов - они размещаются только в вершинах параллелепипеда, на саму ячейку приходится всего один узел. Сложной же считается ячейка, в которой узлы расположены не только в вершинах, но и внутри самой ячейки или на ее гранях. При этом число узлов, приходящихся на ячейку, больше одного.                 

Элементарную ячейку можно выбирать по-разному, однако при этом рекомендуется придерживаться следующих правил:              

- она должна наилучшим образом отражать симметрию решетки;

- иметь прямые углы (если это возможно);

- обладать наименьшей площадью.

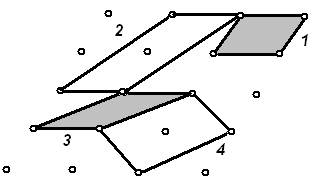На рис.4 показано различное изображение элементарных решеток для косоугольной плоской сетки. Параллелограммы 1 и 3 - это примеры простой элементарной ячейки, а остальные (2 и 4) характеризуют сложные ячейки. При этом из предложенных вариантов наиболее предпочтительной следует считать элементарную ячейку 1, поскольку она построена с использованием двух кратчайших расстояний и хорошо отражает симметрию сетки.

 

 

Рис.4. Схема, иллюстрирующая возможность различного выбора примитивной элементарной ячейки

 

Применительно к плоской сетке принято использовать следующий важный показатель - ретикулярную плотность сетки. Под этим понимается число узлов, приходящихся на единицу площади. Так, для простой ячейки она составляет 1, а для сложной - больше 1.