Вторая производная от функции, заданной параметрически

Пусть функция задана параметрическими уравнениями . Известно, что первая производная находится по формуле

.

Найдем вторую производную, пользуясь определением второй производной и правилом дифференцирование сложной функции:

,

т.е.

,

или

.

Пример. Найти вторую производную функции

 

Решение:                          .

.

3.4. Производная n -го порядка

 

Производная от второй производной функции  называется производной третьего порядка и обозначается  или . Аналогично определяются производные любого порядка. Таким образом,

.

Производные, начиная со второй, называются производными высших порядков.

 

Дифференциал функции

Пусть функция  дифференцируема в точке x, т.е. . Тогда, по теореме о связи между функцией и её пределом, можно записать , где  при , или . Таким образом, приращение функции  представляет собой сумму двух слагаемых  и , которые являются бесконечно малыми при . При этом первое слагаемое есть бесконечно малая функция одного порядка с , т.к. , а второе слагаемое есть бесконечно малая функция более высокого порядка, чем :

.

Произведение , представляющее главную часть приращения функции, линейную относительно , называют дифференциалом функции и обозначают  или :

                                                     .                                                          (*)

Найдем дифференциал функции ; в этом случае ,

и, следовательно,  или . Таким образом, дифференциал  независимой переменной x совпадает с её приращением . В этом случае формулу (*) можно записать так:

                                          .                              (**)

Из этого соотношения следует, что

.

Следовательно, производную  можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.

 

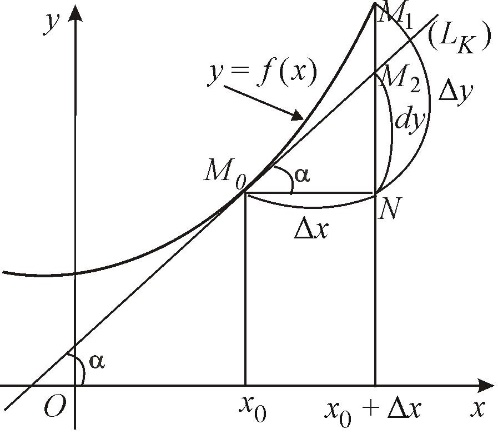
Геометрический смысл дифференциала

Проведем к графику функции  в точке  касательную  и рассмотрим ординату этой касательной для точки  (рис.3). На рисунке , . Из прямоугольного треугольника  имеем:

,  т.е. .

                                                                      

                                                                  Рис.3

 

Но, согласно геометрическому смыслу производной, . Поэтому , а это есть, согласно определению, дифференциал функции, т.е.

.

Таким образом, дифференциал функции геометрически представляет собой приращение ординаты касательной при приращении аргумента .

Приращение функции можно представить в виде

,

или из рис. 3:

,

и если , то и , а, значит и , поэтому можно приближенно считать  равным , т.е.

.

Этим фактом пользуются при приближенных вычислениях.

Пример. Найти приближенное значение приращения функции  при  и .

Решение: .

.

Итак, .

Проверим погрешность вычисления, вычислив приращение функции по формуле

.

Абсолютная погрешность приближения равна

.

 

Правила нахождения дифференциала

 

Пусть  и  две дифференцируемые функции.

1. ; ; C – const;

2. ; ;

3. ; ;

4. ; .