
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальное исчисление функции одной переменнойСтр 1 из 2Следующая ⇒
Дифференциальное исчисление функции одной переменной Определение производной. Пусть функция
Составим отношение приращения функции к приращению аргумента:
Найдем предел этого отношения при Таким образом, по определению
или
Функция Найти производные следующих функций, пользуясь определением производной: 1. 2.
3.
Геометрический смысл производной Проведем секущую

 перпендикулярную перпендикулярную
 , ,
то угловые коэффициенты этих прямых находятся в отношении N:
Механический смысл производной
Скорость прямолинейного движения материальной точки в момент времени t – мгновенная скорость:
Связь между непрерывностью и дифференцируемостью Теорема 1. Функция Доказательство: Так как
 может не иметь в ней производной. может не иметь в ней производной.

Рис.2
Решение:
Правила дифференцирования Теорема 2. Если функции 1. 2. 3. Следствие. Если функция дифференцируема в точке x, а С – const, то Найти производные функций 1. Итак, 2. Итак,
Таблица производных
На практике часто приходится находить производные сложных функций, поэтому заменим в таблице аргумент x на промежуточный аргумент 1. 2. 3. 4. 5. 6. 7.
8. 9. 10. 11. 12.
Производные высших порядков Вторая производная
Пусть функция Таким образом, по определению
Пример. Найти 1. 2. Дифференциал функции Пусть функция
Произведение Найдем дифференциал функции и, следовательно,
Из этого соотношения следует, что
Следовательно, производную
Дифференциальное исчисление функции одной переменной Определение производной. Пусть функция
Составим отношение приращения функции к приращению аргумента:
Найдем предел этого отношения при Таким образом, по определению
или
Функция Найти производные следующих функций, пользуясь определением производной: 1. 2.
3.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 38; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.150.163 (0.027 с.) |
 определена в окрестности точки
определена в окрестности точки  . Дадим аргументу
. Дадим аргументу 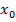 некоторое приращение
некоторое приращение  , тогда функция получит приращение
, тогда функция получит приращение 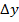 . Тогда при значении аргумента
. Тогда при значении аргумента 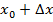 будем иметь
будем иметь  . Найдем приращение функции:
. Найдем приращение функции: .
.
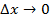 . Если этот предел существует, то его называют производной данной функции
. Если этот предел существует, то его называют производной данной функции 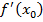 .
. (*)
(*)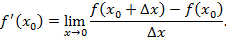
 , имеющая производную в каждой точке интервала
, имеющая производную в каждой точке интервала  , называется дифференцируемой в этом интервале, операция вычисления производной функции называется дифференцированием.
, называется дифференцируемой в этом интервале, операция вычисления производной функции называется дифференцированием. ;
;  , т.е.
, т.е.  .
. ;
;
 ;
;
 к графику функции
к графику функции  . Если
. Если  , то
, то  и
и  т.е. секущая S будет стремиться к положению касательной K. Так как
т.е. секущая S будет стремиться к положению касательной K. Так как  , то
, то  , т.е. производная функции в точке
, т.е. производная функции в точке  равна угловому коэффициенту касательной, проведенной к графику функции в точке
равна угловому коэффициенту касательной, проведенной к графику функции в точке  .
.


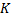



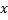

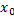
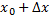
 или
или  , тогда уравнение нормали запишется так:
, тогда уравнение нормали запишется так: .
. .
. , непрерывна в этой точке.
, непрерывна в этой точке. , то по теореме о связи между функцией и ее пределом имеем
, то по теореме о связи между функцией и ее пределом имеем  , где
, где  при
при  . Но если
. Но если  , то и
, то и  , т.е.
, т.е.  , а это значит, что бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции – определение непрерывности функции в терминах приращений.
, а это значит, что бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции – определение непрерывности функции в терминах приращений. – в точке
– в точке  не существует, т.к. левый предел не равен правому пределу и график в этой точке не имеет касательной.
не существует, т.к. левый предел не равен правому пределу и график в этой точке не имеет касательной. и
и  дифференцируемы в точке x, то в этой точке дифференцируемы функции
дифференцируемы в точке x, то в этой точке дифференцируемы функции  ,
,  ,
,  , при этом:
, при этом: ;
; ;
; .
. .
. и
и  , пользуясь теоремой 2.
, пользуясь теоремой 2. ;
; .
. .
. .
. , который является функцией от x:
, который является функцией от x:  , С – const;
, С – const; ;
;
 ;
; ;
; ;
; ;
; ;
; ;
;

 ;
; .
. имеет производную во всех точках интервала
имеет производную во всех точках интервала  . Если функция
. Если функция  дифференцируема в точке
дифференцируема в точке  , то её производную называют второй производной или производной второго порядка функции
, то её производную называют второй производной или производной второго порядка функции  в точке
в точке  и обозначают
и обозначают  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
 .
. .
. . Пусть
. Пусть  , где
, где  , тогда
, тогда  , отсюда
, отсюда  .
. . Пусть
. Пусть  , где
, где  , тогда
, тогда  , отсюда
, отсюда  .
. . Тогда, по теореме о связи между функцией и её пределом, можно записать
. Тогда, по теореме о связи между функцией и её пределом, можно записать  , где
, где  при
при  , или
, или  . Таким образом, приращение функции
. Таким образом, приращение функции  представляет собой сумму двух слагаемых
представляет собой сумму двух слагаемых  и
и  , которые являются бесконечно малыми при
, которые являются бесконечно малыми при  , т.к.
, т.к.  , а второе слагаемое есть бесконечно малая функция более высокого порядка, чем
, а второе слагаемое есть бесконечно малая функция более высокого порядка, чем  .
. , называют дифференциалом функции и обозначают
, называют дифференциалом функции и обозначают  или
или  :
: . (*)
. (*) ; в этом случае
; в этом случае  ,
, или
или  . Таким образом, дифференциал
. Таким образом, дифференциал  независимой переменной x совпадает с её приращением
независимой переменной x совпадает с её приращением  . В этом случае формулу (*) можно записать так:
. В этом случае формулу (*) можно записать так: . (**)
. (**) .
. можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.
можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.


