
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Заявки принимаются к обслуживанию
· в порядке очереди (FIFO, очереди с приоритетами и др.), · в случайном порядке в соответствии с заданными распределениями, по минимальному времени получения отказа · и др. Реальный процесс функционирования СМО следует представлять в виде последовательности фаз обслуживания, выполняемых различными устройствами. Примеры многофазного обслуживания: обслуживание покупателей в магазине (прилавок, касса; технологический процесс – обработка деталей на станках Обслуженная заявка покидает прибор обслуживания и покидает систему (поглотитель заявок), либо движется дальше в соответствии с технологической схемой работы системы. СМО классифицируются: · По числу каналов обслуживания – одноканальные и многоканальные; · По числу фаз обслуживания – на однофазные и многофазные; · По наличию обратно связи – на разомкнутые и замкнутые; · По наличию и типу очереди – без очередей (с потерей заявок), системы с неограниченным ожиданием (по времени и по очереди) и системы с ограниченным ожиданием (по времени и длине очереди); · По принципу формирования очередей – с общей очередью, с несколькими очередями; · По наличию отказов – системы с отказами, системы без отказов; · По приоритетам – системы со статичными приоритетами (дисциплина обслуживания может быть различной, FIFO) и система с динамическим приоритетом, которые имеют 3 разновидности: а) относительный приоритет – заявка высокого приоритета ожидает конца обслуживания заявки более низкого приоритета; б) абсолютный приоритет – заявка с более высоким приоритетом при поступлении незамедлительно вытесняет заявку с более низким приоритетом; в) смешанный приоритет – если заявка с более низким приоритетом обслуживалась в течение времени меньше, чем критическое, то применяется абсолютный приоритет, иначе-относительный.
Любая модель строится для того, чтобы оценить какие-то показатели качества. Показатели качества обслуживания:
Сущность метода имитационного моделирования для СМО:
Используются специальные алгоритмы, позволяющие вырабатывать случайные реализации потоков событий и моделировать процессы функционирования обслуживающих систем. Далее осуществляется многократное воспроизведение, реализация случайных процессов обслуживания и статистическая обработка на выходе - оценка показателей качества обслуживания.
Вопрос 18. Моделирование случайных событий и дискретных величин. Моделирование случайных событий. Простейшими случайными объектами при статистическом моделировании систем являются случайные события. Рассмотрим особенности их моделирования. Пусть имеются случайные числа случайной величины x, равномерно распределенной в интервале (0,1). Необходимо реализовать случайное событие А, наступающее с заданной вероятностью р. Определим А как событие, состоящее в том, что выбранное значение
Тогда вероятность события А будет Процедура моделирования в этом случае состоит в выборе значений Таким же образом можно рассмотреть группу событий. Пусть А1, А2,..., Aj — полная группа событий, наступающих с вероятностями р1, р2,..., рs, соответственно. Определим Аm как событие, состоящее в том, что выбранное значение
где
Процедура моделирования испытаний в этом случае состоит в последовательном сравнении случайных чисел
Моделирование дискретных случайных величин. Рассмотрим особенности преобразования для случая получения дискретных случайных величин. Дискретная случайная величина hпринимает значения yl≤ y2 ≤... ≤ yj≤... с вероятностями р1,р2,..., рj..., составляющими дифференциальное распределение вероятностей
При этом интегральная функция распределения
Fh(y) = 0; y<y1. (4.19) Для получения дискретных случайных величин можно использовать метод обратной функции. Если x, — равномерно распределенная на интервале (0, 1) случайная величина, то искомая случайная величина hполучается с помощью преобразования
где Алгоритм вычисления по (4.19) и (4.20) сводится к выполнению следующих действий:
если х1<р, то h=у1, иначе если х2<р1+р2, то h=у2 иначе, ………………… (4.21) если ………………… При счете по (4.21) среднее число циклов сравнения
Вопрос 24. Стратегическое планирование машинных экспериментов с моделями систем.
Существует два основных варианта постановки задачи планирования имитационного эксперимента: 1. из всех допустимых выбирается такой план, который позволяет получить наиболее достоверное значение отклика при фиксированном числе опытов. 2. выбирается такой допустимый план, при котором статистическая оценка функции отклика может быть получена с заданной точностью при минимальном объеме испытаний. Решение первой задачи – стратегическое планирование эксперимента. При стратегическом планировании решаются две основные задачи: 1)идентификация факторов; 2)выбор уровня факторов. Под идентификацией факторов понимается их ранжирование по степени влияния на значение наблюдаемой переменной. Факторы обычно разделяются на две группы: - первичные (те факторы, в исследовании влияния которых экспериментатор заинтересован); - вторичные (факторы, которые не являются предметом исследования, но влиянием которых нельзя пренебречь). В процессе идентификации факторов мало влияющие факторы могут не учитываться. Выбор уровней факторов производится с учетом двух противоречивых требований: 1. выбранные факторы должны перекрывать (заполнять) изучаемый диапазон его значений. 2. общее количество уровней по всем факторам не должно приводить к чрезмерному размеру (V) моделирования. Способы построения стратегического плана: Эксперимент, в котором реализуются все возможные сочетания факторов называется ПФЭ (полный факторный эксперимент). Общее число различных комбинаций уровней (точек) в ПФЭ вычисляется по формуле:
где li – число уровней для i-го фактора, k – число факторов. Если число уровней для всех факторов одинаково и равно L, то N=Lk. Недостаток ПФЭ – большие временные затраты на проведение эксперимента, поэтому используются частичные факторные эксперименты (ЧФЭ). Рассмотрим некоторые ЧФЭ: рандомизированный план – предполагает выбор сочетания уравнений для каждого прогона случайным образом. При этом фиксируется число экспериментов, которым экспериментатор считает возможным ограничиться.
латинский план («латинский квадрат») используется в том случае, когда проводится эксперимент с одним первичным фактором и несколькими вторичными. эксперимент с изменением факторов по одному. Один из факторов пробегает все свои уровни в то время, как остальные факторы остаются фиксированными. дробный факторный эксперимент. Каждый фактор имеет два уровня (верхний и нижний), поэтому общее число вариантов эксперимента N=2k. Пример латинского плана. Рассматриваются 3 фактора: А,В,С. А – первичный; В,С – вторичные.
План строится таким образом, чтобы в каждой строке и в каждом столбце таблицы данный уровень был представлен только один раз. По данному плану необходимо провести 16 экспериментов. N=16. Для ПФЭ N было бы 43=64. Экономия в 4 раза. Пример дробного факторного эксперимента. k=0
0 – нижний уровень фактора 1 – верхний уровень ЧФЭ N=22=4.
Вопрос 25. Тактическое планирование машинных экспериментов с моделями систем (проблема определения начальных условий и их влияния на достижение установившегося результата, проблема обеспечения точности и достоверности результатов моделирования). Планирование машинных экспериментов – один из этапов имитационного моделирования. План определяет объем и порядок проведения вычислений на ЭВМ, приемы накопления и статистической обработки результатов моделирования системы S Тактическое планирование эксперимента с машинной моделью Тактическое планирование представляет собой определение способа проведения каждой серии испытаний машинной модели Мм, предусмотренных планом эксперимента. Для тактического планирования также имеется аналогия с внутренним проектированием системы S, но опять в качестве объекта рассматривается процесс работы с моделью Ми. Мы системы S связано с вопросами эффективного использования выделенных для эксперимента машинных ресурсов и определением конкретных способов проведения испытаний модели Мы, намеченных планом эксперимента, построенным при стратегическом планировании. Тактическое планирование машинного эксперимента связано прежде всего с решением следующих проблем: 1) определения начальных условий и их влияния на достижение установившегося
результата при моделировании; 2) обеспечения точности и достоверности результатов моделирования; 3) уменьшения дисперсии оценок характеристик процесса функционирования моделируемых систем; 4) выбора правил автоматической остановки имитационного эксперимента с моделями систем Проблема определения начальных условий и их влияния на достижение установившегося результата при моделировании. Первая проблема при проведении машинного эксперимента возникает вследствие искусственного характера процесса функционирования модели Мм, которая в отличие от реальной системы S работает эпизодически, т. е. только когда экспериментатор запускает машинную модель и проводит наблюдения. Поэтому всякий раз, когда начинается очередной прогон модели процесса функционирования системы S, требуется определенное время для достижения условий равновесия, которые соответствуют условиям функционирования реальной системы. * Таким образом, начальный период работы машинной модели Мм искажается из-за влияния начальных условий запуска модели. Для решения этой проблемы либо исключается из рассмотрения информация о модели Мм, полученная в начальной части периода моделирования (0, Т), либо начальные условия выбираются так, чтобы сократить время достижения установившегося режима. Все эти приемы позволяют только уменьшить, но не свести к нулю время переходного процесса при проведении машинного эксперимента с моделью Мм. * Проблема обеспечения точности и достоверности результатов моделирования. Решение второй проблемы тактического планирования машинного эксперимента связано с оценкой точности и достоверности результатов моделирования (при конкретном методе реализации модели, например, методе статистического моделирования на ЭВМ) при заданном числе реализаций (объеме выборки) или с необходимостью оценки необходимого числа реализаций при заданных точности и достоверности результатов моделирования системы S. Как уже отмечалось, статистическое моделирование системы S — это эксперимент с машинной моделью Мм. Обработка результатов подобного имитационного эксперимента принципиально не может дать точных значений показателя эффективности Е системы S; в лучшем случае можно получить только некоторую оценку Е такого показателя. При этом экономические вопросы затрат людских и машинных ресурсов, обосновывающие целесообразность статистического моделирования вообще, оказываются тесно связанными с вопросами точности и достоверности оценки показателя эффективности Е системы S на ее модели Мм Таким образом, количество реализаций N при статистическом моделировании системы S должно выбираться исходя из двух основных соображений: определения затрат ресурсов на машинный эксперимент с моделью Мм (включая построение модели и ее машинную реализацию) и оценки точности и достоверности результатов эксперимента с моделью системы S (при заданных ограничениях не ресурсы). Очевидно, что требования получения более хороших оценок и сокращения затрат ресурсов являются противоречивыми и при планировании машинных экспериментов на базе статистического моделирования необходимо решить задачу нахождения разумного компромисса между ними.
Из-за наличия стохастичности и ограниченности числа реализаций N в общем случае вероятность того, что неравенство
выполняется, называется достоверностью оценки
Величина ε0 = ε/Е называется относительной точностью оценки, а достоверность оценки соответственно будет иметь вид
Для того чтобы при статистическом моделировании системы по заданным Е (или Е0) и Q определить количество реализаций N или, наоборот, при ограниченных ресурсах (известном N) найти необходимые Е и Q, следует детально изучить соотношение (6.7). Сделать это удается не во всех, случаях, так как закон распределения вероятностей величины N = tφ2p(1-p)/(p2ε02) = tφ2(l-р)/(ε02р). (6.10) Соотношение (6.10 – точность результатов моделирования) наглядно иллюстрирует специфику статистического моделирования систем, выражающуюся в том, что для оценивания малых вероятностей р с высокой точностью необходимо очень большое число реализаций N. В практических случаях для оценивания вероятностей порядка 10- k целесообразно количество реализаций выбирать равным 10k+1. Очевидно, что даже для сравнительно простых систем метод статистического моделирования приводит к большим затратам машинного времени.
Вопрос 26. Задачи обработки результатов моделирования.
Успех имитационного эксперимента с моделью системы существенным образом зависит от правильного решения вопросов обработки и последующего анализа и интерпретации результатов моделирования. Особенно важно решить проблему текущей обработки экспериментальной информации при использовании модели для целей автоматизации проектирования систем. При обработке результатов машинного эксперимента с моделью Мм наиболее часто возникают следующие задачи: · определение эмпирического закона распределения случайной величины · проверка однородности распределений · сравнение средних значений и дисперсий переменных, полученных в результате моделирования, и т. д. Эти задачи с точки зрения математической статистики являются типовыми задачами по проверке статистических гипотез. Задача определения эмпирического закона распределения случайной величины наиболее общая из перечисленных, но для правильного решения требует большого числа реализаций N. В этом случае по результатам машинного эксперимента находят значения выборочного закона распределения Fэ (y) (или функции плотности fэ(y)) и выдвигают нулевую гипотезу Н0, что полученное эмпирическое распределение согласуется с каким-либо теоретическим распределением. Проверяют эту гипотезу Н0 с помощью статистических критериев согласия Колмогорова, Пирсона, Смирнова и т. д., причем необходимую в этом случае статистическую обработку результатов ведут по возможности в процессе моделирования системы S на ЭВМ. Для принятия или опровержения гипотезы выбирают некоторую случайную величину U, характеризующую степень расхождения теоретического и эмпирического распределения, связанную с недостаточностью статистического материала и другими случайными причинами. Закон распределения этой случайной величины зависит от закона распределения случайной величины η и числа реализаций N при статистическом моделировании системы S. Если вероятность расхождения теоретического и эмпирического распределений P{Uт≥U} велика в понятиях применяемого критерия согласия, то проверяемая гипотеза о виде распределения H0 не опровергается. Выбор вида теоретического распределения F(y) (или f(у)) проводится по графикам (гистограммам) Fэ(y) (или fэ(у)), выведенным на печать или на экран дисплея. Особенности использования при обработке результатов моделирования системы S на ЭВМ ряда критериев согласия можно рассмотреть на основе критериев согласия Колмогорова, Пирсона, Стьюдента, Фишера и Смирнова. Хотя указанные выше оценки искомых характеристик процесса функционирования системы S, полученные в результате машинного эксперимента с моделью Мм, являются простейшими, но охватывают большинство случаев, встречающихся в практике обработки результатов моделирования системы для целей ее исследования и проектирования.
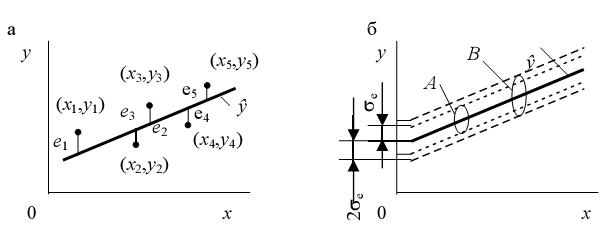
Вопрос 30. Регрессионный анализ результатов моделирования. Регрессионный анализ дает возможность построить модель, наилучшим образом соответствующую набору данных, полученных в ходе машинного эксперимента с системой S. Под наилучшим соответствием понимается минимизированная функция ошибки, являющаяся разностью между прогнозируемой моделью и данными эксперимента. Такой функцией ошибки при регрессионном анализе служит сумма квадратов ошибок. Пример: Рассмотрим особенности регрессионного анализа результатов моделирования при построении линейной регрессионной модели. На рис. 2, а показаны точки xi, yi, где y - величина, предсказываемая регрессионной моделью.
Рис. 2 Построение линейной регрессионной модели
Требуется получить такие значения коэффициентов b0 и b1 при которых сумма квадратов ошибок модели является минимальной. На рисунке ошибка ei, Обозначим Для получения b0 и b1, при которых функция F0 является минимальной, применяются обычные методы математического анализа. Условием минимума является Дифференцируя F, получаем
Решая систему этих двух линейных алгебраических уравнений, можно получить значения b0 и b1. В матричном представлении эти уравнения имеют вид:
Решая это уравнение получаем
где N — число реализаций при моделировании системы. Соотношения для вычисления b0 и b1 требуют минимального объема памяти ЭВМ для обработки результатов моделирования. Обычно мерой ошибки регрессионной модели служит среднее квадратичное отклонение
Для нормально распределенных процессов приблизительно 67 % точек находится в пределах одного отклонения σе от линии регрессии и 95 % в - пределах 2 σе(трубки А и B соответственно на рис. 2, б). Для проверки точности оценок b0и b1, в регрессионной модели могут быть использованы, например, критерии Фишера (F-распределение) и Стьюдента (t-распределение). Аналогично могут быть оценены коэффициенты уравнения регрессии и для случая нелинейной аппроксимации.
Вопрос 33
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 84; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.110.0 (0.089 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
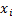 т. е. возможные значения
т. е. возможные значения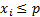 (условие 1)
(условие 1)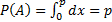 . Противоположное событие
. Противоположное событие 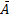 состоит в том, что
состоит в том, что 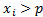 . Тогда Р(
. Тогда Р( 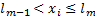 (условие 2)
(условие 2) . Тогда
. Тогда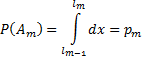
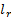 . Исходом испытания оказывается событие Аm, если выполняется условие 2. Эту процедуру называют определением исхода испытания по жребию в соответствии с вероятностями р1,p2,…, ps
. Исходом испытания оказывается событие Аm, если выполняется условие 2. Эту процедуру называют определением исхода испытания по жребию в соответствии с вероятностями р1,p2,…, ps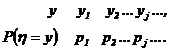 (4.18)
(4.18)
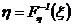 , (4.20)
, (4.20) — функция, обратная Fh.
— функция, обратная Fh.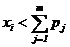 то h=уm, иначе
то h=уm, иначе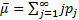
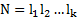
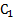
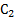
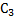
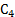
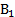
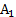
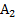
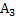
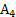
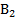
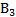

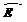 ≠Е. При этом величина Е называется точностью (абсолютной) оценки:
≠Е. При этом величина Е называется точностью (абсолютной) оценки: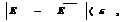 (6.6)
(6.6)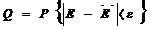 (6.7)
(6.7)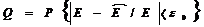 .
.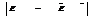 для многих практических случаев исследования систем установить не удается либо в силу ограниченности априорных сведений о системе, либо из-за сложности вероятностных расчетов. Основным путем преодоления подобных трудностей является выдвижение предположений о характере законов распределения случайной величины
для многих практических случаев исследования систем установить не удается либо в силу ограниченности априорных сведений о системе, либо из-за сложности вероятностных расчетов. Основным путем преодоления подобных трудностей является выдвижение предположений о характере законов распределения случайной величины  , т.е. оценки показателя эффективности системы S.
, т.е. оценки показателя эффективности системы S.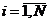 , полученные в машинном эксперименте. Mм системы S. Делаем предположение, что модель результатов машинного эксперимента графически может быть представлена в виде прямой линии
, полученные в машинном эксперименте. Mм системы S. Делаем предположение, что модель результатов машинного эксперимента графически может быть представлена в виде прямой линии 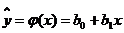 ,
,
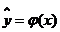 .
.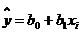 ,
,  , а функция ошибки
, а функция ошибки 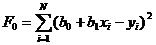 .
. .
.
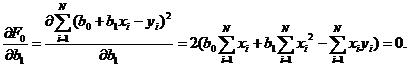
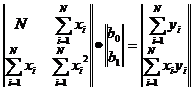 .
.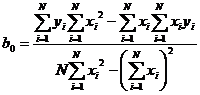 ,
, ,
,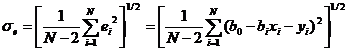 .
.


