Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод параллельного переноса. Построить трапецию по четырём сторонам.
Задача 1.
И д е я. Произвести параллельный перенос боковой стороны трапеции. У к а з а н и е. После параллельного переноса боко- вой стороны трапеции получится треугольник, ко- торый легко построить по трём сторонам.
Р е ш е н и е. Пусть даны стороны трапеции BC = a, AB = b, CD = c, AD = d. Перенесём боковую сторону b вдоль основания a, получим параллелограмм ABCA.
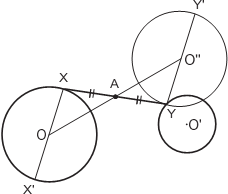
Задача 2. Между двумя окружностями провести отрезок, делящийся пополам в данной точ- ке A.
У к а з а н и е. Рассмотреть окружности с центрами O и O. Пусть XY – искомый отрезок. Продолжить XO до X и перенести первую окружность так, чтобы X совместилась с Y. Указ ани е. Так как XY Y X – параллелограмм с диагональю XY, то точка A – её середина.
Для решения задачи надо перенести первую окружность вдоль прямой OA на расстояние OO = 2 OA. Проведя прямую через полученную точку пересечения Y и точку A, найдём точку X. Задача может иметь одно, два или ни одного решения.
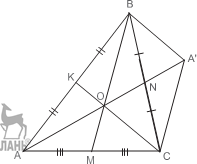
Задача 3. Построить треугольник, зная m a, m c и ∠(m b, a). И д е я. Предположить, что треугольник построен, и провести дополнительное построение. У к а з а н и е. Пусть даны медианы AN = m a и CK = m c треугольника ABC и угол MBC = α. Пусть медианы пересекаются в точке O. Достроить Δ BOC до параллелограмма BOCA.
Р е ш е н и е. Пусть даны медианы AN = m a и CK = m c треугольника ABC и угол MBC = α. Пусть медианы пересекаются в точке O. Достроим Δ BOC до параллелограмма BOCA.
1)
2) Вершину A получим, отложив на прямой OA отрезок OA = OA. 3) Вершину C получим, отложив на прямой BN отрезок NC = NB.
Задача 4.
И д е я. Диагонали параллелограмма делятся точкой пересечения пополам. Ук азани е. Отложить на прямой OA отрезок AB = OA. Через точку B провести прямые, па- раллельные сторонам угла.
Р е ш е н и е. Отложим на прямой OA отрезок AB = OA. Через точку B проведём прямые, параллельные сторонам угла. Получим параллелограмм OCBD. Так как диагонали параллелограмма точкой пересечения делятся пополам, то CA = AD. Следовательно, CD – искомая прямая.
Задача 5.
У к а з а н и е. Пусть даны длины диагоналей AC и BD и длина боковой стороны CD. Перене- сти диагональ BD в отрезок CE вдоль основа- ния BC. У к а з а н и е. Треугольник ACE легко постро- ить по двум сторонам и углу между ними.
CD. Перенесём диагональ BD в отрезок CE вдоль основания BC. В треугольнике ACE боковые стороны равны диагоналям трапеции, а угол ACE равен углу между диагоналями. Следовательно, этот треугольник мы можем построить. Для того чтобы найти вершину D, надо сделать засечку циркулем из C на прямой AE радиусом, равным длине боковой стороны CD. После этого, достроив Δ CDE до параллелограмма, получим вершину B.
Задача 6. Построить четырёхугольник, зная две диагонали, две противолежащие стороны и угол между ними. И д е я. Использовать параллельный перенос одной из диагоналей четырёхуголь- ника.
Задача 7. Через данную точку M провести прямую так, чтобы разность расстояний до неё от двух данных точек A и B была равна данной длине. И д е я. Предположить, что прямая проведена, опустить на неё перпендикуляры из данных точек и использовать параллельный перенос. Указ ани е. Пусть A и B – основания перпендикуляров, опущенных из точек A и B на искомую прямую. Перенести отрезок A B параллельно в отрезок AC. У к а з а н и е. Прямоугольный треугольник ABC легко построить по гипотенузе AB и катету CB, равному данной в условии задачи разности расстояний.
Треугольник ABC является прямоугольным с извест- ной гипотенузой AB и катетом CB, равным данной в условии задачи разности расстояний. Для того чтобы построить нужную прямую, надо сна- чала построить треугольник ABC по катету и гипотенузе, а потом провести через точку M прямую, параллельную отрезку AC.
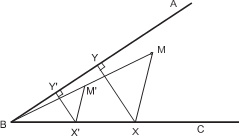
Задача 8. В данный остроугольный треугольник вписать прямоугольник с наименьшей диа- гональю (одна сторона прямоугольника лежит на основании треугольника).
И д е я. Вершину треугольника перенести параллельно основанию так, чтобы по- лучился прямоугольный треугольник. У к а з а н и е. Пусть в треугольник ABC вписан прямоугольник KLMN. Перене- сти вершину C параллельно AB так, чтобы треугольник ABC был прямоуголь- ным. Так как LL = KK, прямоугольник KLMN при этом перейдёт в равный ему прямоугольник K L M A. У к а з а н и е. Диагональ прямоугольника K L M A будет принимать минималь- ное значение в случае, когда AL ⊥ BC.
Диагональ прямоугольника K L M A будет принимать минимальное значение в случае, ко- гда AL ⊥ BC. То есть в Δ ABC надо про-
вести AL ⊥ BC и построить прямоугольник K L M A с такой диагональю. Этот прямоуголь- ник и будет искомым прямоугольником. Осталось совершить обратный параллельный перенос прямоугольника вдоль AB на расстоя- ние L L.
Задача 9. Даны три параллельные прямые. Провести через данную точку секущую так, что- бы разность отрезков между параллелями была равна заданной величине.
И д е я. Использовать методы симметрии и параллельного переноса.
В целом построение выглядит так: снача- ла строим m, потом из произвольной точки K прямой k делаем засечку на m радиусом, равным d. Так мы получим точку M. Оста- лось провести через данную точку A прямую, параллельную построенной секущей.
Построить трапецию ABCD, зная боковую сторону CD, угол между диагоналя- ми, расстояние между параллельными сторонами и отрезок, соединяющий сере- дины боковых сторон.
И д е я. Пусть трапеция построена. Перенести диагональ BD в отрезок CE па- раллельно вдоль основания BC. У к а з а н и е. Треугольник ACE можно построить по основанию, высоте и из- вестному углу.
Р е ш е н и е. Пусть нам дана высота трапеции, длина средней линии и длина бо- ковой стороны CD. Перенесём диагональ BD в отрезок CE параллельно вдоль основания BC.
сечку циркулем из C на прямой AE радиусом, равным длине боковой стороны CD. После этого, достроив Δ CDE до параллелограмма, получим вершину B.
Задача 11. Построить треугольник по b, c и m a.
И д е я. Использовать вспомогательное построение: достроить треугольник до па- раллелограмма.
У к а з а н и е. Построить Δ ABA по трём известным сторонам.
ив его до параллелограмма, получить вершину C.
Задача 12. Построить четырёхугольник, зная его стороны и отрезок, соединяющий середины двух противоположных сторон.
У к а з а н и е. Построить Δ BCY по трём сторонам. У к а з а н и е. Построить Δ CXD по медиане и двум сторонам.
Ре ше ни е. Пусть ABCD – искомый четырёхугольник, а точки X и Y взяты таким образом, что четырёхугольники ABXC и ACY D являются параллелограм- мами. Наша цель – построить вспомогательный параллелограмм BXY D, а потом восстановить четырёхугольник ABCD.
В теоретической части было показано, что диагонали параллелограмма BXY D вдвое больше средних линий исходного четырёхугольника.
Теперь построим точки X и D. Обозначим через E середину стороны BY и рассмотрим Δ CXD. Точки C и E уже построены. То есть в Δ CXD дана медиана и стороны CX (CX = AB)и CD, которые равны данным в условии задачи сторо- нам четырёхугольника. Построив Δ CXD по медиане и двум сторонам (см. пред. задачу), мы определим точки X и D. А достроив Δ BCX до параллелограмма, получим вершину A.
Задача 13. Построить четырёхугольник, зная четыре его стороны и угол между двумя про- тивоположными сторонами.
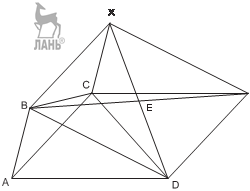
И д е я. Использовать вспомогательный параллелограмм, стороны которого па- раллельны и равны диагоналям искомого четырёхугольника. У к а з а н и е. Построить сначала вспомогательный параллелограмм BXY D, сто- роны которого параллельны и равны диагоналям искомого четырёхугольника ABCD. У к а з а н и е. Построить Δ CXD по двум сторонам и углу между ними. У к а з а н и е. Построить Δ BCY по медиане CE и двум сторонам BC и CY.
Р е ш е н и е. Построим сначала вспомогательный параллелограмм BXY D, сто- роны которого параллельны и равны диагоналям искомого четырёхугольника ABCD.
ить точки B и Y, построим Δ BCY по медиане CE и двум сторонам BC и CY (CY = AD), которые равны сторонам четырёхугольника ABCD. Достроив Δ BCX до парал- лелограмма, получим вершину A.
Задача 14. Построить биссектрису угла, вершина которого недоступна.
У к а з а н и е. Расстояния от построенных прямых до соответствующих сторон уг- ла будут одинаковыми.
В силу равенства углов при параллель- ных прямых биссектрисой построенного угла будет также прямая m. Отметим, что расстояния между параллельными прямы- ми будут равными. Следовательно, если вершина O недо- ступна, то надо провести две прямые на равном расстоянии от сторон исходного угла и для угла с уже доступной верши- ной построить биссектрису.
Задача 15. Даны две точки A и B и между ними две параллели m и n. Провести между этими параллелями в данном направлении отрезок CD так, чтобы сумма AC + + CD + BD была минимальной.
У к а з а н и е. Пусть отрезок CD с концами на параллелях m и n проведён в заданном на- правлении. Перенести его параллельно в отрезок C B, тогда AC + CD + BD = AC + CC + BC . Р е ш е н и е. Пусть отрезок CD с концами на па- раллелях m и n проведён в заданном направле- нии. Перенесём его параллельно в отрезок C B, тогда AC + CD + BD = AC + CC + BC . Следовательно, задача свелась к отысканию на прямой m точки C такой, что сумма AC + CC минимальна. Значит, в качестве точки C надо взять точку пересечения прямой m с отрезком AC.
На окружности даны две точки A и B. В данном направлении провести хорду XY так, чтобы сумма хорд AX и BY была равна заданной величине.
И д е я. Провести хорду AA параллельно заданному в условии направлению и использовать метод симметрии и спрямления для нахождения точки Y.
Ре ш е н и е. Пусть X, Y – искомые точки. Про- ведём хорду AA в заданном в условии направ- лении. Отрезок A Y = AX, так как у вписанной трапеции AA YX боковые стороны равны. Итак, всё свелось к построению точки Y та- кой, что BY + Y A имеет заданную длину, а эта задача была решена нами в предыдущем разделе методом симметрии и спрямления.
Задача 17. Построить прямоугольник с данной стороной так, чтобы его стороны проходили через четыре заданные точки.
И д е я. Пусть прямоугольник построен. Проанализировать, что нам известно. У к а з а н и е. Пусть даны точки A, B, C, D и отрезок длины a. Рассмотреть пер- пендикуляр AH, опущенный из точки A на противоположную сторону искомого прямоугольника. У к а з а н и е. Треугольник ACH можно построить по известной гипотенузе AC и катету AH = a.
Треугольник ACH мы можем построить по известной гипотенузе AC и катету AH = a. Для того чтобы построить искомый прямоугольник, надо через точки D и B провести прямые, па- раллельные AH, а через A и C – прямые, парал- лельные HC. Точки пересечения этих прямых и будут вершинами искомого прямоугольника.
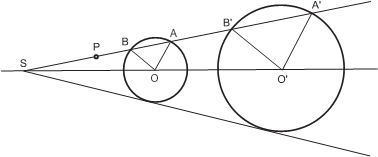
Задача 18. Даны две окружности и прямая. Провести параллельно этой прямой секущую, отсекающую в окружностях хорды, сумма которых равна заданному отрезку дли- ны s.
У к а з а н и е. Рассмотрим две окружности с центрами O 1 и O 2 и прямую m.
перейдёт в хорду BE. Ук азани е. Пусть P и Q – основания перпендикуляров, опущенных из точек O 1 и O 2 на прямую AD. Отрезок PQ = s/ 2.
Пусть P и Q – основания перпендику- ляров, опущенных из точек O 1 и O 2 на прямую AD. Отрезок PQ = s/ 2.
пендикулярно m. Так мы найдём точку H. Отложив от неё отрезок H O 2
= s/ 2, получим центр перенесённой окружности O 2. Эта окружность пересечёт первую окружность в точке B. В результате осталось провести прямую через B парал- лельно прямой m.
Метод подобия
И д е я. Построить треугольник, по- добный искомому. У к а з а н и е. По двум данным углам построить Δ A B C. Р е ш е н и е. Сначала по двум дан- ным углам построим Δ A B C. Для того чтобы построить искомый треугольник A BC с высотой h a, доста- точно в треугольнике A B C на прямой, содержащей высоту A H , отложить отрезок A H = h a и через точку H провести прямую BC, параллельную B C . Задача 2. Построить окружность, касающуюся сторон данного угла и проходящую через заданную внутри него точку.
И д е я. Построить вспомогательную окружность с центром O, касающуюся сто- рон угла. У к а з а н и е. Соединить вершину угла S с заданной точкой A.
Р е ш е н и е. Построим вспомогательную окружность с центром O, касающуюся сторон угла.
Соединим вершину угла S с заданной точкой A. Пусть A — точка пересечения прямой SA с окружностью. Проведём через A прямую параллельно отрезку A O. Она пересечёт луч SO в точке O – центре искомой окружности.
Задача 3.
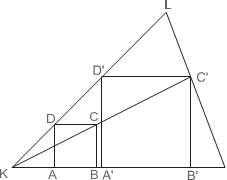
И д е я. Построить треугольник (со вписанным в него равносторонним треуголь- ником), подобный данному, а потом с помощью гомотетии преобразовать вписан- ный треугольник в искомый. Указ ани е. Вписать в угол A равносторонний Δ P Q S.
Р е ш е н и е. На сторонах угла A возьмём произвольно точки P , Q и построим равносторонний Δ P Q S. Если точка S попала на сторону BC, то наша задача выполнена. Если нет, то проведём прямую через точку S параллельно BC. Пусть B ,C – точки пересечения этой прямой с лучами AB и AC соответственно.
AB C подобны с коэффициентом по- AB добия k =
AB , поэтому если мы применим гомотетию с этим коэффи-
AB (это мы умеем делать). Ана- логично строятся точки Q и S.
Задача 4. В данный треугольник вписать квадрат.
И д е я. Построить вспомогательный квадрат и воспользоваться преобразованием гомотетии. У к а з а н и е. Пусть дан треугольник KLM. Построить вспомогательный квадрат
Построить треугольник по α, β, r.
И д е я. Вписать окружность данного радиуса в треугольник, подобный данному. У к а з а н и е. По двум данным углам построить Δ A BC, подобный искомому. В угол B вписать окружность данного радиуса.
Задача 6. Через данную точку провести прямую, отсекающую от двух данных окружностей хорды, пропорциональные их радиусам. И д е я. Использовать свойства центра подобия окружностей. У к а з а н и е. Воспользоваться тем, что любая секущая, проведённая через центр подобия окружностей, отсекает от окружностей хорды, пропорциональные ради- усам. Р е ш е н и е. Воспользуемся тем, что любая секущая, проведённая через центр подобия окружностей, пересекает окружности таким образом, что треугольники ABO и A B O являются гомотетическими. Проведём через центр подобия S и данную точку P прямую. Из подобия треугольников ABO и A B O следует про- порциональность соответствующих отрезков.
Дан угол ABC и точка M внутри него. Найти на стороне BC точку X, равно- удалённую от AB и точки M. И д е я. Использовать преобразование гомотетии.
У к а з а н и е. Провести через точку M прямую, параллельную прямой M X.
З а м е ч а н и е. Задача решается аналогичным образом, если вместо перпендику- ляра XY требуется провести отрезок, образующий с AB заданный угол и нахо- дящийся в известном отношении к MX.
Задача 8. Даны три точки A, B и C, не лежащие на одной прямой. Провести прямую, пересекающую отрезок AC в точке X, а отрезок BC в точке Y таким образом, что AX = XY = Y B. И д е я. Построить четырёхугольник, подобный четырёхугольнику AXY B.
У к а з а н и е. Четырёхугольник AX Y B (AX = X Y = Y B = d) подобен искомому.
Р е ш е н и е. Построим четырёхугольник, подобный искомому четырёхугольнику AXY B. На стороне AC отложим отрезок AX произвольной длины d, а на сто- роне BC – отрезок BY = AX = d. Проведем окружность с центром в X радиу- сом d и прямую через Y параллельно AB. Пусть Y – точка их пересечения. Про- ведём через неё прямую параллельно BC, получим точки B и C. Треугольник
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 575; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.82.79 (0.289 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Построить трапецию по четырём сторонам.
Построить трапецию по четырём сторонам.
 Общая последовательность действий такова.
Общая последовательность действий такова.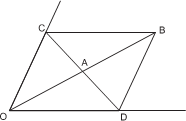 Через точку A внутри угла провести прямую так, чтобы отрезок, заключённый между сторо- нами, делился точкой A пополам.
Через точку A внутри угла провести прямую так, чтобы отрезок, заключённый между сторо- нами, делился точкой A пополам.
 И д е я. Использовать параллельный перенос од- ной из диагоналей трапеции.
И д е я. Использовать параллельный перенос од- ной из диагоналей трапеции.
 У к а з а н и е. Треугольник XCD можно по- строить по двум сторонам и углу между ними. У к а з а н и е. Треугольник BDX легко по- строить по трём сторонам.
У к а з а н и е. Треугольник XCD можно по- строить по двум сторонам и углу между ними. У к а з а н и е. Треугольник BDX легко по- строить по трём сторонам.
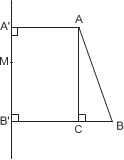

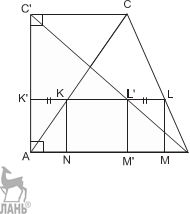 Р е ш е н и е. Пусть в треугольник ABC вписан прямоугольник KLMN. Перенесём вершину C параллельно AB так, чтобы треугольник ABC был прямоугольным. Так как LL = KK, пря- моугольник KLMN при этом перейдёт в равный ему прямоугольник K L M A.
Р е ш е н и е. Пусть в треугольник ABC вписан прямоугольник KLMN. Перенесём вершину C параллельно AB так, чтобы треугольник ABC был прямоугольным. Так как LL = KK, пря- моугольник KLMN при этом перейдёт в равный ему прямоугольник K L M A.

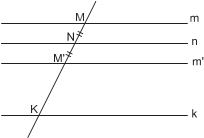
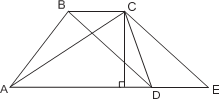 Рассмотрим треугольник ACE. Так как средняя линия трапеции равна полу- сумме оснований, отрезок AE равен двум средним линиям, угол ACE равен углу между диагоналями, а высота Δ ACE рав- на высоте трапеции. Следовательно, этот треугольник мы можем построить по осно- ванию, высоте и известному углу. Для того чтобы найти вершину D, надо сделать за-
Рассмотрим треугольник ACE. Так как средняя линия трапеции равна полу- сумме оснований, отрезок AE равен двум средним линиям, угол ACE равен углу между диагоналями, а высота Δ ACE рав- на высоте трапеции. Следовательно, этот треугольник мы можем построить по осно- ванию, высоте и известному углу. Для того чтобы найти вершину D, надо сделать за-
 Р е ш е н и е. Рассмотрим треугольник ABC с данными сторонами AC = b, AB = c и медианой AM = m a. От- ложим точку A на прямой AM так, что M A = AM. Четырёхугольник ABA C будет параллелограммом со сторонами, равными b и c, и диагональю AA = 2 m a. Для построения Δ ABC надо сначала построить Δ ABA по трём известным сторонам, а потом, достро-
Р е ш е н и е. Рассмотрим треугольник ABC с данными сторонами AC = b, AB = c и медианой AM = m a. От- ложим точку A на прямой AM так, что M A = AM. Четырёхугольник ABA C будет параллелограммом со сторонами, равными b и c, и диагональю AA = 2 m a. Для построения Δ ABC надо сначала построить Δ ABA по трём известным сторонам, а потом, достро-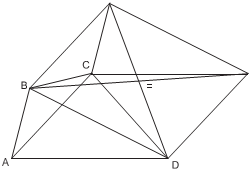



 Угол XCD равен углу меж- ду прямыми, содержащими сторо- ны AB и CD (см. теоретическую часть). Следовательно, в Δ CXD стороны CX (CX = AB) и CD равны сторонам исходного четырёх-
Угол XCD равен углу меж- ду прямыми, содержащими сторо- ны AB и CD (см. теоретическую часть). Следовательно, в Δ CXD стороны CX (CX = AB) и CD равны сторонам исходного четырёх-
 532 Указания и решения
532 Указания и решения
 Р е ш е н и е. Пусть стороны угла лежат на прямых k и n, пересекающихся в точке O. Через точку O, лежащую на биссектрисе m, проведём прямые, параллельные сторо- нам угла.
Р е ш е н и е. Пусть стороны угла лежат на прямых k и n, пересекающихся в точке O. Через точку O, лежащую на биссектрисе m, проведём прямые, параллельные сторо- нам угла.
 У к а з а н и е. Надо построить точку Y такую, что BY + Y A имеет заданную длину, а эта зада- ча была решена в предыдущем разделе методом симметрии и спрямления.
У к а з а н и е. Надо построить точку Y такую, что BY + Y A имеет заданную длину, а эта зада- ча была решена в предыдущем разделе методом симметрии и спрямления.
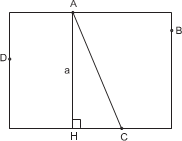 Р е ш е н и е. Пусть даны точки A, B, C, D и от- резок длины a. Рассмотрим перпендикуляр AH, опущенный из точки A на противоположную сторону искомого прямоугольника.
Р е ш е н и е. Пусть даны точки A, B, C, D и от- резок длины a. Рассмотрим перпендикуляр AH, опущенный из точки A на противоположную сторону искомого прямоугольника.
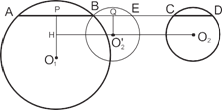
 В целом построение выглядит следую- щем образом. Проведём через O 2 прямую параллельно m и через O 1 прямую пер-
В целом построение выглядит следую- щем образом. Проведём через O 2 прямую параллельно m и через O 1 прямую пер- Задача 1.
Задача 1. 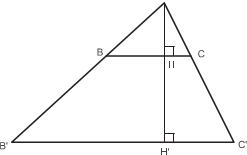 Построить треугольник по двум уг- лам и высоте, проведённой из третье- го угла.
Построить треугольник по двум уг- лам и высоте, проведённой из третье- го угла.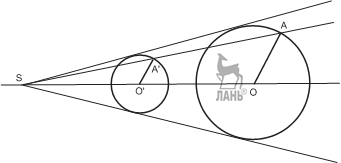
 Заметим, что треугольники ABC и
Заметим, что треугольники ABC и



 З а м е ч а н и е. Задача решается аналогичным обра- зом, если вместо угла α задано отношение сторон a и c.
З а м е ч а н и е. Задача решается аналогичным обра- зом, если вместо угла α задано отношение сторон a и c.