Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод симметрии и спрямления. Построить треугольник, зная P, α и h a .
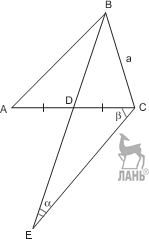
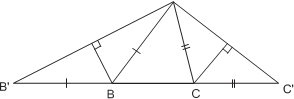
Задача 1. Построить треугольник, зная P, α и h a. И д е я. Развернуть треугольник на прямую. У к а з а н и е. Пусть треугольник ABC уже построен. На прямой BC отложить отрезки BB = AB и CC = AC. Ук азани е. Δ AB C легко построить по стороне, противолежащему углу и вы- соте. Р е ш е н и е. Пусть треугольник ABC уже построен. На прямой BC отложим отрезки BB = AB и CC = AC.
Треугольники BB A и CC A равнобедренные с углами при основании соот- β
2 и γ. Следовательно, у треугольника AB C сторона B C = P и
∠ B AC = π β γ = π + α. − 2 − 2 2 2 Таким образом, для того чтобы построить Δ ABC, сначала нам надо построить Δ AB C по стороне, противолежащему углу и высоте. Серединные перпендикуляры к сторонам AB и AC пересекут B C в точках B и C.
Даны две окружности и между ними прямая. Начертить равносторонний тре- угольник так, чтобы две его вершины были на окружностях, а одна из высот лежала на данной прямой.
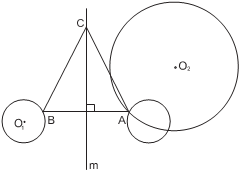
И д е я. Отразить одну из окружностей относительно прямой. У к а з а н и е. Точка пересечения окружностей – одна из вершин искомого тре- угольника. Р е ш е н и е. Пусть даны окружности с центрами O 1 и O 2 и прямая m. Отразим первую окружность относительно прямой. Пусть A – точка пересечения отражён- ной окружности со второй окружностью, а B – симметричная ей точка на первой окружности.
Теперь отметим на прямой m точку C так, чтобы AC = AB. Треугольник ABC будет равносторонним, и его высота будет лежать на m. В зависимости от числа точек пересечения окружностей задача может иметь одно, два или ни одного решения.
Дана прямая m и две точки A и B по одну сторону от неё. Найти на m такую точку X, чтобы AX составлял с m угол, вдвое больший, чем BX. И д е я. Построить окружность, касающуюся прямой m с центром в точке B.
Точка пересечения этой касательной с прямой m и есть искомая точка (см. рису- нок).
Задача 4. Внутри угла даны точки A и B. Построить равнобедренный треугольник, осно- вание которого лежит на одной стороне угла, вершина – на другой, а боковые стороны проходят через точки A и B.
И д е я. Отразить точку A симметрично относительно прямой OM в точку A , где O – вершина угла, а M – вершина искомого равнобедренного треугольника. Ук азани е. Выразить ∠ A MB через величину данного угла.
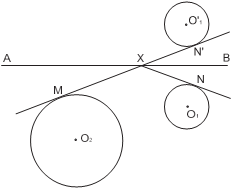
Задача 5. Дана прямая AB и две окружности, лежащие по одну сторону от прямой. Найти на прямой AB точку, касательные из которой составляют с этой прямой равные углы.
И д е я. Отразить одну из окружностей относительно прямой AB. У к а з а н и е. Провести внутреннюю касательную ко второй окружности и отра- жённой окружности.
ми O 1 и O 2 пересечет прямую AB в точке X. Обозначим через M, N, N точки касания окружностей с центрами O 2, O 1, O 1 с касательными, проведённы- ми из точки X. Заметим, что ∠ NXB = ∠ N XB, как симметричные, и ∠ MXA = ∠ N XB, как вертикальные. Следовательно, точка X есть искомая точка.
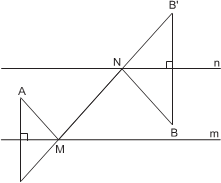
Задача 6. Точки A и B расположены между параллельными прямыми m и n. Постройте точки M ∈ m, N ∈ n так, чтобы длина ломаной AM NB была наименьшей.
У к а з а н и е. Соединить получившиеся точки A и B. Р е ш е н и е. Рассмотрим A – отражение относительно m точки A и B – отражение относительно n точки B.
В данную окружность вписать прямоугольник, зная разность основания и высоты.
И д е я. Диагональ прямоугольника является диамет- ром окружности. У к а з а н и е. Отложить на большей стороне прямо- угольника известную разность сторон.
Р е ш е н и е. Рассмотрим прямоугольник ABCD, впи- санный в окружность. Отметим на AB точку C та- кую, что BC = BC.
Точку B можно получить как точку пересечения прямой AC с окружностью, а вершину D как точку, симметричную B относительно центра окружности.
Задача 8. Построить треугольник по стороне, прилежащему углу и разности остальных сто- рон.
И д е я. Предположить, что искомый треугольник построен, и проанализировать данные. У к а з а н и е. Отложить на большей из двух неизвестных сторон отрезок, равный меньшей стороне.
Р е ш е н и е. Пусть требуемый треугольник ABC построен по известной стороне AB = c, углу A, равному α, и разности двух других сторон, равной b − a. Отложим на стороне CA отрезок CC, равный CB. Тогда AC = b − a. Треугольник ABC легко построить по сторонам c, b − a и углу между ними α.
Так как треугольник BCC равнобедренный, точку C можно найти как точку пересечения серединного перпендикуляра к BC с прямой AC.
Задача 9. Построить четырёхугольник ABCD, зная его стороны, если диагональ AC делит угол A пополам.
И д е я. Отразить вершину D относительно прямой AC. У к а з а н и е. Треугольник BCD легко построить по трём сторонам.
стороны BC, CD = CD, BD = AB − AD
Вершину A можно получить, отложив от B на прямой BD отрезок, равный BA. Вер- шина D есть отражение D относительно прямой AC.
Задача 10.
И д е я. Отразить основание одного из пер- пендикуляров относительно основания. У к а з а н и е. Показать, что искомая сумма равна высоте, проведённой к боковой стороне треугольника.
дует параллельность прямых AM BC. Так как M D и DN перпендикулярны па- раллельным прямым, точки M ,D и N ле- жат на одной прямой и их сумма равна рас- стоянию между этими прямыми. В результате сумма DM + DN = DM + DN равна расстоянию от точки A до стороны BC, то есть высоте, проведённой к боковой стороне треугольника.
Задача 11. Найти сумму перпендикуляров, опущенных из точки, взятой внутри равносторон- него треугольника, на его стороны.
И д е я. Воспользоваться результатом предыдущей задачи.
DM + DN = BH , где BH – одна из равных высот равностороннего треугольника Δ A BC. Так как DK = H H, то DM + DN + DK = BH + H H = BH, то есть сумма перпендикуляров из точки внутри равностороннего треугольника равна высоте исходного треугольника.
Задача 12.
И д е я. Пусть задача решена и точка X уже най- дена. Отложить на прямой BX отрезок XC = AX. У к а з а н и е. Треугольник ABC легко построить.
α
2 Следовательно, треугольник ABC мы можем построить по основанию AB, противолежащему α углу 2 и боковой стороне, равной a. Его сторона BC пересечёт окружность в искомой точке X.
Задача 13. На окружности даны точки A и B. Отыскать на ней точку X такую, что AX − BX = a, где a – заданный отрезок.
И д е я. Пусть задача решена и точка X уже найдена. Отложить на отрезке AX отрезок XC = BX. У к а з а н и е. Треугольник ABC легко построить.
2 угол α = ∠ AXB известен как угол, опирающий- ся на известную дугу. Рассмотрим треугольник ABC. У него из- вестны основание AB, сторона AC = a и угол
2 и продолжив его сторону AC до пересечения с окружностью, мы получим искомую точку X.
Задача 14. Найти геометрическое место точек, сумма расстояний от которых до двух данных пересекающихся прямых равна заданному отрезку.
И д е я. Использовать одну из предыдущих задач про сумму расстояний от точки на основании равнобедренного треугольника до боковых сторон. У к а з а н и е. Отложить от точки пересечения прямых во все четыре стороны отрезки, равные заданному отрезку. У к а з а н и е. Соединить последовательно получившиеся четыре точки на прямых и показать, что получившийся прямоугольник – искомое ГМТ.
Согласно одной из предыдущих за- дач, сумма расстояний от любой точки на основании равнобедренного треуголь- ника до боковых сторон равна высоте, проведённой к боковой стороне. Следова- тельно, искомое ГМТ есть четыре отрез- ка, являющиеся сторонами прямоугольника ABCD.
Задача 15.
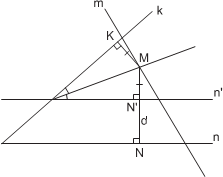
И д е я. Провести прямую, параллельную одной из сторон угла и отстоящую от неё на расстоянии, равном длине данного в условии задачи отрезка. У к а з а н и е. Показать, что биссектриса нового угла пересечёт данную прямую в искомой точке.
Действительно, если через K, N и N обозначить основания перпендикуляров на соответствующих прямых, то MN − MK = MN + N N − MK = N N = d. Задача 16.
И д е я. Предположить, что искомая окружность уже построена, и проанализиро- вать, что известно. У к а з а н и е. В треугольнике, вершинами которого являются центры трёх окруж- ностей, известны сторона, угол против этой стороны и разность двух других сто- рон. У к а з а н и е. Использовать одну из предыдущих задач.
R 1 − R 2. А такую задачу мы умеем решать (см. одну из предыдущих задач).
Задача 17.
И д е я. Отложить от основания высоты BD на её продолжении отрезок DE, равный основанию AC треугольника.
1
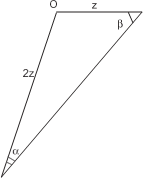
2 Ре ш е н и е. Пусть в Δ ABC с высотой BD стороны AB = BC = a, BD + AC = s. Отложим на продол- жении BD отрезок DE = AC. Так как DE = 2 DC, то tg ∠ DEC = 1 / 2. Для того чтобы построить треугольник ABC, сна- чала построим отрезок BE = s, отложим от него угол 1 α = arctg , потом на стороне этого угла сделаем за-
сечку из точки B радиусом a. Так мы получим точ- ку C. Вершину A можно получить как отражение точки C относительно прямой BE.
Задача 18. Построить треугольник по a, m b + b и ∠(m b, b). И д е я. Отложить от основания медианы BD на её продолжении отрезок DE, равный стороне AC треугольника. Указ ани е. Зная угол ∠(m b, b), легко построить угол DEC. У к а з а н и е. Треугольник BCE легко построить по двум сторонам и углу BEC.
Итак, для построения треугольника ABC сначала надо построить отрезок BE = s, потом отложить от него угол α и на стороне этого угла сделать засечку из точки B радиусом a. Из полученной точки C под углом β к EC проведём луч. Он пересечёт BE в точке D. Отложив AD = DC, найдём вершину A.
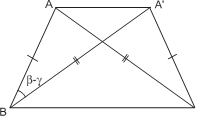
Задача 19. Построить треугольник по b, c и β − γ. И д е я. Рассмотреть треугольник, симметричный данному, с общей третьей сто- роной. Ук азани е. Пусть в Δ ABC стороны AC = b, AB = c. Рассмотреть Δ A BC, симметричный исходному, со сторонами A B = b, A C = c. У к а з а н и е. Треугольник AA B легко построить по двум сторонам и углу между ними.
Следовательно, треугольник AA B мы
шину C, проведём через B прямую параллельно AA и отложим на ней C так, что AC = b.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 195; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.147.190 (0.147 с.) |
 ветственно
ветственно 2
2



 У к а з а н и е. Отразить построенную ок- ружность относительно прямой m и про- вести к отражённой окружности касатель- ную через точку A.
У к а з а н и е. Отразить построенную ок- ружность относительно прямой m и про- вести к отражённой окружности касатель- ную через точку A. Ре ше ни е. Пусть O – вершина данного угла α, MH – высота искомого треуголь- ника. Отразим точку A относительно пря- мой OM, получим A. Имеем
Ре ше ни е. Пусть O – вершина данного угла α, MH – высота искомого треуголь- ника. Отразим точку A относительно пря- мой OM, получим A. Имеем

 И д е я. Отразить точки A и B относи- тельно прямых m и n соответственно.
И д е я. Отразить точки A и B относи- тельно прямых m и n соответственно.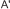 Ломаные AM NB и A MNB имеют одинаковую длину. Эта длина принимает своё минимальное значение в случае, когда точки M и N лежат на отрезке A B. Сле- довательно, искомые M и N суть точки пе- ресечения прямых m и n с отрезком A B.
Ломаные AM NB и A MNB имеют одинаковую длину. Эта длина принимает своё минимальное значение в случае, когда точки M и N лежат на отрезке A B. Сле- довательно, искомые M и N суть точки пе- ресечения прямых m и n с отрезком A B.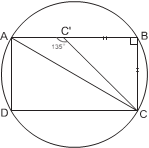


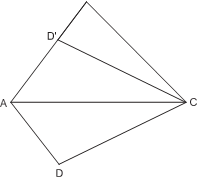
 Р е ш е н и е. Рассмотрим четырёхугольник ABCD. Так как ∠ CAD = ∠ CAB, то D (от- ражение точки D относительно AC) будет лежать на прямой AB. В треугольнике BCD
Р е ш е н и е. Рассмотрим четырёхугольник ABCD. Так как ∠ CAD = ∠ CAB, то D (от- ражение точки D относительно AC) будет лежать на прямой AB. В треугольнике BCD 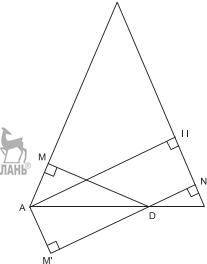
 Найти сумму перпендикуляров, опущенных на стороны равнобедренного треугольника из точки, взятой на основании.
Найти сумму перпендикуляров, опущенных на стороны равнобедренного треугольника из точки, взятой на основании.
 У к а з а н и е. Провести через точку, из которой опущены перпендикуляры, прямую, параллельную одной из сторон треугольника.
У к а з а н и е. Провести через точку, из которой опущены перпендикуляры, прямую, параллельную одной из сторон треугольника.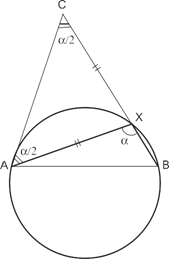
 нии равны.
нии равны. Р е ш е н и е. Пусть задача решена и точка X уже найдена. Отложим на отрезке AX отре- зок XC = BX. В равнобедренном треугольнике
Р е ш е н и е. Пусть задача решена и точка X уже найдена. Отложим на отрезке AX отре- зок XC = BX. В равнобедренном треугольнике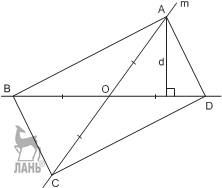
 Ре ш е н и е. Пусть прямые m и n пере- секаются в точке O. Отметим на прямой m точку A, находящуюся на заданном расстоянии d от прямой n. Отложим от- резки, равные OA, на других лучах, вы- ходящих из O. Получим четыре точки A, B, C и D, которые являются верши- нами четырёх равнобедренных треуголь- ников с общей вершиной O.
Ре ш е н и е. Пусть прямые m и n пере- секаются в точке O. Отметим на прямой m точку A, находящуюся на заданном расстоянии d от прямой n. Отложим от- резки, равные OA, на других лучах, вы- ходящих из O. Получим четыре точки A, B, C и D, которые являются верши- нами четырёх равнобедренных треуголь- ников с общей вершиной O.

 Построить равнобедренный треугольник, зная его бо- ковую сторону a и сумму высоты с основанием s.
Построить равнобедренный треугольник, зная его бо- ковую сторону a и сумму высоты с основанием s. двум сторонам и углу, равному arctg.
двум сторонам и углу, равному arctg.
 2
2