
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Бесконечные пределы в конечной точке
Говорят, что функция
 Геометрический смысл: График функции Геометрический смысл: График функции  для всех для всех 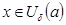 лежит вне горизонтальной полосы лежит вне горизонтальной полосы 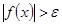 . .
 Пример. Найти пределы функции Пример. Найти пределы функции  при при  . .
Решение.
  ; ; 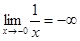 . .
Рис.4 Конечный предел в бесконечности
Говорят, что число А есть предел функции Пример. Найти пределы функции Решение. Бесконечный предел в бесконечности
 при при  . .
Решение.
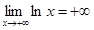
Рис.5 Замечание 1. Замечание 2. Не всякая функция при Бесконечно малые функции. Теоремы о бесконечно малых.
Определение. Если Примеры 1. Функция 2. Функция 3. Функция На «языке Замечание. Нельзя смешивать постоянное очень малое число с бесконечно малой функцией (б.м.ф. или б.м.). Теорема 2.1. Если Пример. Функция Теорема 2.2. Сумма бесконечно малых при Теорема 2.3. Произведение бесконечно малой при
Следствие 1. Если Следствие 2. Произведение бесконечно малой при Теорема 2.4. Частное от деления бесконечно малой при 2.2. Связь между функцией и ее пределом.
Теорема 2.5. Если функция Обратная теорема 2.6. Если функция
Теоремы о пределах. Теорема 2.7. Пусть функции 1. 2. 3. Следствие 1. Постоянный множитель можно выносить за знак предела:
Следствие 2. Предел целой положительной степени равен степени от предела:
Примеры. 1. 2. Не всякая функция, даже ограниченная, имеет предел (см. выше замечание 2 п.1.5). Во многих вопросах математического анализа бывает достаточно только убедиться в существовании предела функции. В этих случаях пользуются признаками существования предела.
Теорема 2.8 (о пределе промежуточной функции). Пусть функции
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 53; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.125.219 (0.013 с.) |
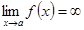 , если
, если  .
.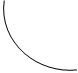 В этом случае функцию
В этом случае функцию  .
.


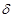



 и пишут
и пишут 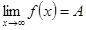
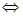
 .
. при
при  . (см. рис.4)
. (см. рис.4)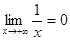 ;
;  .
. Говорят, что функция
Говорят, что функция 
 .
.

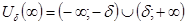 ;
; 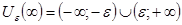 .
.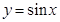 и
и  никакого предела не имеют.
никакого предела не имеют. , то функция
, то функция 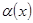 называется бесконечно малой при
называется бесконечно малой при 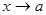 (или просто бесконечно малой).
(или просто бесконечно малой). является бесконечно малой при
является бесконечно малой при 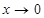 .
.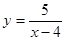 является бесконечно малой при
является бесконечно малой при 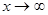 .
.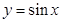 является бесконечно малой при
является бесконечно малой при  .
.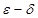 »: функция
»: функция  является бесконечно малой при
является бесконечно малой при  .
. – б.м. при
– б.м. при  – бесконечно большая при
– бесконечно большая при 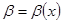 – бесконечно большая при
– бесконечно большая при 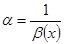 – бесконечно малая при
– бесконечно малая при 
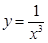 – бесконечно большой при
– бесконечно большой при 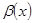 – бесконечно малые при
– бесконечно малые при 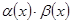 – бесконечно малая при
– бесконечно малая при  – бесконечно малая, где
– бесконечно малая, где  .
.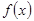 имеет конечный предел в точке
имеет конечный предел в точке  , то она может быть представлена в виде суммы своего предела и бесконечно малой при
, то она может быть представлена в виде суммы своего предела и бесконечно малой при  , то
, то 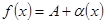 , где
, где  имеют конечные пределы в точке
имеют конечные пределы в точке  .
.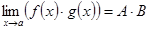 .
. при
при 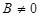 .
.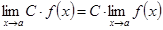 .
. .
. .
.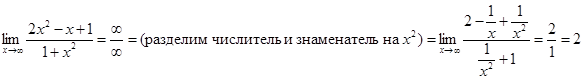 .
. ,
, 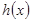 определены в некоторой окрестности точки а, за исключением, может быть, точки а, и функции
определены в некоторой окрестности точки а, за исключением, может быть, точки а, и функции 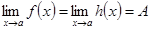 . Пусть, кроме того, выполняются неравенства
. Пусть, кроме того, выполняются неравенства 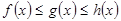 . Тогда
. Тогда .
.


