
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
После завершения этой лабораторной работы необходимо владеть навыкамиСодержание книги
Поиск на нашем сайте
Обзор главного меню системы Общение пользователя с системой MathCAD происходит на некотором промежуточном математически ориентированном языке визуального программирования – входном языке. Многие математические записи в этом языке вводятся просто выводом шаблонов соответствующих операторов и функций. Необходимо лишь точное описание алгоритма решения задачи на привычном математическом языке. MathCAD ориентирован на автоматическое составление программ сложных математических вычислений вводом и заполнением шаблонов математических операций. Сама программа при этом генерируется автоматически. Операторы – специальные символы, указывающие на выполнение тех или иных операций над данными – операндами. Последние могут быть константами или переменными – объектами с именами, хранящие данные определенного типа и значения. Наиболее известны арифметические операторы, например, сложения +, вычитания -, умножения *, деления / и др. Функция – объект входного языка, имеющий имя и параметры, указываемые в круглых скобках. Имя функции отождествляется с соответствующей математической функцией – например, sin(x) – это функция вычисления синуса аргумента x. Отличительной чертой функции является преобразование данных, представленных в виде входных параметров, и возврат значения (результата вычисления функции) в ответ на обращение к ней. Операторы и функции используются для создания математических выражений – формул, которые могут вычисляться в численном или символьном виде. Рассмотрим окно MathCAD. Верхняя строка содержит указание на имя пакета и название документа в котором вы работаете. Далее идет главное меню, кнопки быстрого управления и окно редактирования, в котором можно создавать документ, представляющий собой набор формул для математических расчетов, текстовых областей и графических объектов. Пункты главного меню: File – работа с файлами, сетью Интернет и электронной почтой; Edit – редактирование документов; View – изменение средств обзора и включения/выключения элементов интерфейса; Insert – установка вставок объектов и их шаблонов (включая графику); Format – изменение формата (параметров) объектов; Math – управление процессом вычислений; Graphics – работа с графическим редактором; Symbolic – выбор операций символьного процессора; Window – управление окнами системы; Books – работа с электронными книгами; Help – работа со справочной базой данных о системе. Основные возможности главного меню дублируются кнопками быстрого управления, размещенными в панелях. Их можно выводить на экран или убирать с него с помощью соответствующих опций позиции View главного меню. Имеются три такие панели: 1) панель вывода палитр математических знаков и функций, 2) панель инструментов дублирует наиболее распространенные команды и операции, 3) панель форматирования для выбора типа размера шрифтов и способа выравнивания текстовых комментариев. ¿ - вызвать на экран все палитры математических символов, для чего выбрать команду меню View Þ Toolbars и «включить» каждую палитру: Arithmetic – арифметические операции и элементарные функции; Evaluation – знаки отношений, шаблоны операторов; Graph – шаблон графиков различного типа; Matrix – шаблон векторов и матриц и действий над ними; Calculus – операторы производных, интегралов, сумм, произведений и др.; Programming – средства программирования; Greek – греческие буквы; Symbolic – ключевые слова и операторы символьных вычислений; Modifier – дополнительные операции палитры Symbolic. ¿ Закрыть все панели, кроме Math, нажать каждую из кнопок с пиктографическим изображением на этой панели. & С помощью таких наборных панелей можно вводить в документы практически все известные математические символы и операторы. Для установки с их помощью необходимого шаблона (объекта) достаточно поместить курсор (красный крестик) в желаемое место окна редактирования и затем активизировать пиктограмму нужного шаблона, установив на нее курсор мышки и нажав ее левую клавишу. В составе сложных шаблонов присутствуют шаблоны, указывающие места ввода отдельных параметров и данных. Они имеют вид небольших черных прямоугольников. ¿ Используя наборные панели вывести шаблоны Работа с формульным редактором. Система MathCAD интегрирует в себе три редактора: формульный, текстовый и графический. Для запуска формульного редактора достаточно установить курсор мыши в любом свободном месте окна редактирования и щелкнуть левой клавишей. Появится визир в виде маленького красного крестика. Его можно перемещать клавишами перемещения курсора. Не путать визир с курсором мыши! Визир указывает место, с которого можно начинать набор формул – вычислительных блоков. В области формул визир превращается в синий уголок, указывающий направление и место ввода. При вводе бинарного оператора по другую сторону знака операции автоматически появляется заполнитель в виде черного прямоугольника. В это место вводят очередной операнд. Для управления порядком операций используют скобки. Чтобы выделить элементы формулы, которые в рамках операции должны рассматриваться как единое целое, используют клавишу ПРОБЕЛ. При каждом ее нажатии уголковый курсор «расширяется», охватывая элементы формулы, примыкающие к данному. Блоки документа и порядок их выполнения. Каждое математическое выражение, график или текстовая область с комментариями образуют блоки. Блоки имеют обычно невидимые границы. & Опираясь на понятие блока можно сформулировать важный принцип работы системы MathCAD – блоки выполняются строго поочередно с просмотром их слева – направо и сверху – вниз. В ходе исполнения документа блоки просматриваются в указанном порядке, распознаются, компилируются и затем уже исполняются. Если в каком-то блоке N используются данные, получаемые в блоках Ni, то все блоки Ni при просмотре должны располагаться так, чтобы они были прочитаны и выполнены до обнаружения блока N. Каждая формула образует отдельный блок, обозначенный рамкой! Пусть необходимо вычислить определенный интеграл. 1) Установить визир в то место экрана, где должен быть помещен шаблон. 2) Вывести панель операторов математического анализа и выбрать пиктограмму с изображением знака определенного интеграла. 3) В шаблоне определенного интеграла 4 черных прямоугольника: для ввода верхнего и нижнего пределов интегрирования, для задания подынтегральной функции и для указания имени переменной по которой идет интегрирование. 4) Для ввода данных необходимо установить указатель мыши на нужный шаблон и ввести данные. 5) Установите знак равенства после полученного выражения и увидите результат вычисления. Задача_1. Вычислить а) Задача_2. Вычислить Работа с текстовым редактором. Текстовый редактор позволяет задавать текстовые комментарии, что делает документ с формулами и графиками более понятным В простейшем случае для ввода текстового редактора достаточно ввести символ “ (кавычка) (на англ.яз.). В появившийся прямоугольник можно начать вводить текст. В текстовом блоке визир имеет вид красной вертикальной черты. Текст можно редактировать общепринятыми средствами. Рекомендуется выбрать нужный тип, начертание и размер шрифта перед началом ввода текста сразу после появления красной вертикальной черты - это можно сделать с помощью команды FORMAT Þ Text. Для редактирования текста или отдельной его части необходимо предварительно выделить требуемый фрагмент. ¿ - Написать заголовок лабораторной работы шрифтом зеленого цвета, размером 14 пт, выбрав начертание – полужирный курсив. Работа со вставками – Insert. Установка любого объекта в окно редактирования называется вставкой (Insert). MathCAD реализует различные механизмы вставки – от выводов шаблона объекта до вставки объекта с помощью связывания с приложением, создавшим объект. При активизации команды меню Insert появляется подменю со следующими операциями: Graph – вставка шаблонов графики с выбором их из подменю; Matrix... – вставка шаблонов матриц и векторов; Function... – вставка шаблонов встроенных функций; Unit... – вставка единиц измерения размерных величин; Picture... – вставка шаблона рисунка; Math Region – вставка в текстовую область шаблона математической области для создания неисполняемого комментария в виде математической формулы; Text Region – вставка текстовой области; Page Break – вставка линии обрыва страницы (горизонтальная черта); Hyperlink – вставка гиперссылки; Reference... – вставка обращения к заданному файлу; Component.. – вставка других компонентов системы; Object... – вставка объекта с установлением динамической связи с порождающим его приложением. ¿ - Используя опцию Text Region набрать заголовок лабораторной работы шрифтом красного цвета, размером 12 пт. & Вставка функций из окна с перечнем функций гарантирует синтаксически верное написание функции. Для вставки функции необходимо выбрать команду меню INSERT Þ Function. В появившемся окне в разделе Function Category (категории функций) выбрать нужный вам раздел. После чего выбрать нужную функцию из предложенной библиотеки в окне Function Name. В нижнем окне описывается формат выбранной функции. Например, для вычисления логарифмической функции необходимо набрать в круглых скобках вначале аргумент, а затем через запятую основание. Задача_3. Вычислить а) Для вычисления предела использовать вместо знака равенства знак ®. Для набора символа ¥ использовать сочетание клавиш Shift+Ctrl+Z. ¿ Установите границы ваших блоков, используя команду меню VIEW Þ Region. Если ваши блоки перекрываются, устраните перекрытия командой меню FORMAT Þ Separate Region (разделить области). ¿ Сохранить лабораторную работу в своей папке под именем Лаб_1. mcd.
Работа с переменными & Важным объектом входного языка MathCADявляются переменные – поименованные области памяти, несущие некоторые значения (численные, строковые или символьные), поскольку каждая переменная использованная в выражении должна быть предварительно определена. С переменными связано понятие присваивания им значений. Символ присваивания :=. Чтобы найти значение некоторого выражения при заданном значении x необходимо: присвоить переменной x нужное значение, записать выражение, используя переменную x. Длянабора на клавиатуре символа присваивания необходимо набрать знак двоеточия. Задача_1. Найдем значение выражения ¿ _1. Для решения в среде MathCAD набрать в рабочей области: x:=3
Задача_2. Найти значения выражений: а) б) Задание ранжированных переменных. Часто возникает необходимость в задании ряда значений. Например, для вычисления факториала N!=1×2×3×…× (N -1)× N нужно сформировать ряд чисел од 1 до N с шагом 1 и перемножить их. Упорядоченный ряд значений какой-то переменной (например, абсциссы x) нужен для построения графика функции – MathCAD строит графики по точкам, соединяя их отрезками прямой. & Для создания таких рядов используются ранжированные переменные. В самом простом случае для создания такой переменной используется выражение: <Имя переменной>:=<Начальное значение>..<Конечное значение>, символ .., указывающий на изменение переменной в заданных пределах (диапазон) выводится набором на клавиатуре символа точки с запятой (;). Если <начальное значение> меньше <конечного значения>, то шаг изменения +1, в противном случае –1. & Для создания ранжированной переменной общего вида используется выражение: <Имя переменной>:=<Начальное значение>, <Начальное значение + Шаг>..<Конечное значение>. Шаг изменения переменной должен быть положительный. Вывод на экран таблицы значений выражения, содержащего ранжированную переменную. Если после некоторого выражения с ранжированной переменной поставить знак равенства, то после щелчка левой клавишей мыши на экран будет выведена таблица значений этого выражения. Задача_3. Задать ранжированную переменную i в диапазоне от 1 до 5 и вывести ее значения. ¿ _3. 1) Задать i:=1..5. 2) Записать i= 3) Щелкнуть левой кнопкой мыши вне области формулы. Задача_4. Задать ранжированную переменную x в диапазоне от 0 до 3 с шагом изменения 0,5. Вывести таблицу значений x. Задача_5. Задать ранжированную переменную z в диапазоне от –0.5 до 0.5 с шагом изменения 0,25. Вывести таблицу значений z. Задача_6. Задав ранжированную переменную u в диапазоне от 0 до 3 с шагом изменения 0,5, вывести таблицу значений функции Задача_7. Задав ранжированную переменную v в диапазоне от –10 до 10 с шагом изменения 0,1. Вывести таблицу значений переменной v и функции ¿ Сохранить лабораторную работу в своей папке под именем Лаб_2. mcd. Лабораторная работа №3. Символьные вычисления Операции, относящиеся к работе символьного процессора, содержатся в подменю SYMBOLIC S главного меню. Они выполняются в командном режиме. Чтобы символьные операции выполнялись процессору необходимо указать, над каким выражением это должно проводиться, т.е. надо выделить выражение. Для некоторых операций следует не только указать выражение, к которому она относится, но и наметить (выделить) переменную, относительно которой выполняется символьная операция. Само выражение в таком случае не выделяется. & Символьные вычисления можно также выполнять, используя палитру Symbolic, вызываемую командой меню VIEW Þ Toolbars Þ Symbolic. В этом случае после набранного выражения, нужно вызвать на палитре нужную команду. Если действие выполняется надо всем выражением, то его необходимо выделить уголковым курсором. Если действие выполняется над некоторой переменной (или выражением), то справа от выбранной команды появляется черный шаблон, в котором необходимо указать переменную (выражение) относительно которой выполняются преобразования. В некоторых командах этот шаблон рекомендуется удалять. Операции с выражениями: & Evaluate (выбор: SYMBOLIC Þ Evaluate) – вычислить выражение с выбором способа вычисления из подменю: § Evaluate Þ Evaluate Symbolically – выполнить символьное вычисление выражения; § Evaluate Þ Floating Point Evaluation – вычислить арифметическое выражение, используя числа с плавающей точкой; § Evaluate Þ Complex Evaluation – выполнить вычисления в комплексном виде. & Simplify – упростить выделенное выражение с выполнением сокращения подобных слагаемых, приведения к общему знаменателю, использования основных тригонометрических тождеств и т.д. Задача_1. Упростить выражение ¿ _1. I способ. 1) Набрать выражение, выделить его. 2) Вызвать палитру Symbolic командой меню VIEW Þ Toolbars Þ Symbolic. 3) Выбрать в палитре операцию Simplify, после того как появится знак ® нажать клавишу Enter. II способ. 1) Набрать выражение и выделить его. 2) Выбрать опцию меню SIMBOLICS Þ Simplify. Задача_2. Упростить выражения двумя способами: а) в)
& Expand – раскрыть выражение. Задача_3. Раскрыть выражение ¿ 1) Набрать выражение. 2) Вызвать палитру Symbolic. 3) Выбрать в палитре операцию Expand, после слова Expand в появившемся черном квадратике указать значение переменной – х. 4) Нажать клавишу Enter. & Factor - разложить число или выражение на множители. Задача_4. Разложить на множители многочлены. ¿ _4. Выполнить указанные операции двумя способами: используя команду меню SIMBOLICS Þ Factor и палитру Symbolic (после выбора команды Factor на палитре удалите черный шаблон ввода справа от Factor и нажмите клавишу Enter). а) & Collect – собрать слагаемые, подобные выделенному выражению, которое может быть отдельной переменной или функцией со своим аргументом. Задача_5. В следующих выражениях приведите подобные слагаемые отдельно по каждой переменной ¿ _5. Выполнить указанные операции двумя способами: используя команду меню SIMBOLICS Þ Collect и палитру Symbolic: а) & Variable (операции с выделенными переменными). Для ряда операций надо знать относительно какой переменной они выполняются. В этом случае нужно выделить переменную, установив на ней маркер ввода. После этого становятся доступными следующие операции: § Solve – найти значения выделенной переменной, при которых содержащее ее выражение становится равным нулю; Задача_6. Решить уравнение ¿ _6. 1) Вызвать палитру Symbolic. 2) Набрать выражение, выбрать в палитре операцию Solve 3) После слова Solve в появившемся черном квадратике указать значение переменной – х, нажать клавишу Enter. Задача_7. Решить уравнения: а) б) § Substitute – заменить указанную переменную содержимым буфера обмена; § Differintiate – дифференцировать выражение, содержащее выделенную переменную, по этой переменной (т.е. вычислить частную производную по данной переменной); Задача_8. Найти частные производные функции ¿ _8. Найдем частную производную по x: 1) Набрать выражение 2) Выделить в нем переменную 3) Выбрать опцию меню SYMBOLICS Þ Variable Þ Differintiate. Аналогично найти частную производную по y. Задача_9. Найти частные производные функций а) § Integrate – интегрировать выражение, содержащее выделенную переменную, по этой переменной; Задача_10. Вычислить неопределенный интеграл ¿ _10. 1) Набрать выражение 2) Выделить в нем переменную 3) Выбрать опцию меню SYMBOLICS Þ Variable Þ Integrate. Задача_11. Вычислить неопределенные интегралы. В последнем выражении привести подобные слагаемые относительно а) § Expand to Series – найти несколько первых членов разложения выражения в ряд Тейлора по степеням выделенной переменной; § Convert to Partial Fraction – разложить на элементарные дроби выражение, которое рассматривается как рациональная дробь относительно выделенной переменной. ¿ Сохранить лабораторную работу в своей папке под именем Лаб_6. mcd. ¿ Индивидуальные задания к лабораторной работе №6 I. Найти частные производные следующих функций 1) 3) 5) 7) 9) 11) 13) 14) II. Вычислить неопределенные интегралы 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) Лабораторная работа №7. Решение систем уравнений Задача_8. Найти точки пересечения параболы ¿ _8. Построить в одном шаблоне графики функций, при этом u изменяется от –5 до 5, а v (u) от 0 до 30. Задачу нахождения точек пересечения можно интерпретировать следующим образом: решить систему из двух уравнений с ограничительными условиями, задающими область поиска корня (u < 0 и u > 0). Решим систему с помощью функции Find. Решим систему уравнений v = u 2 и v =8+3 u при ограничении u < 0. 1) Зададим начальное приближение для u и v: u:=-2 (область описка корня u<0) v:=0. 2) Откроем блок словом Given. 3) Запишем два уравнения, используя жирный знак равенства:
4) Зададим первое ограничение на область поиска корня: u<0. 5) Зададим вектор решений системы
6) Вывести вектор решений на экран. Аналогично найти решения из области u>0. Задача_9. Решить системы уравнений: а) При решении системы уравнений в) функция Find не сможет найти решения (показать это), отсюда будет следовать, что эллипс и прямая не пересекаются. Найдите приближенные решения, используя функцию Minerr. Для решения системы уравнений г) задать начальное приближение x =1, y =1, z =1. Функции Maximize и Minimize. Для поиска значений переменных x 1, x 2,..., xn, при которых некоторая функция f (x 1, x 2,..., xn) имеет максимальное или минимальное значение используются функции Maximize (f, x 1, x 2,..., xn) и Minimize (f, x 1, x 2,..., xn). Они возвращают вектор неизвестных, при котором заданная функция имеет максимальное или минимальное значение, соответственно. & Если необходимы различные ограничительные условия в виде равенств или неравенств, то эти функции должны использоваться в составе блока решения, открываемого словом Given. Задача_10. Найти максимум и минимум функции ¿ _10. Построим график функции h (t). 1) Для поиска максимума функции задать начальное приближение t:=-2. 2) Задать xMax как функцию Maximize, вывести максимальное значение и найти значение функции в точке максимума:
3) Для поиска минимума зададим начальное приближение t:=5. 4) В блоке Given запишем ограничение t>0, задать xMin как функцию Minimize, вывести минимальное значение и найти значение функции в точке минимума:
Задача_11. Построить график поверхности ¿ _11. 1) Построить график поверхности. 2) Задать начальное приближение для обеих! переменных. 3) В блоке Given минимум определится как вектор от (x, y):
4) Вывести значение вектора P на экран и найти значение функции в точке минимума. Задача_12. Построить график поверхности Решение задач линейного программирования. Функции Maximize и Minimize могут широко применяться при решениизадач линейного программирования, которые широко используются в экономических и производственных расчетах. Задача_13. Пусть цех малого предприятия должен изготовить 100 изделий трех типов. Каждого изделия нужно сделать не менее 20 штук. На изделия уходят соответственно 4; 3,4 и 2 кг. металла при его общем запасе 340 кг, а также по 4,75; 11 и 2 кг пластмассы при ее общем запасе 700 кг. Сколько изделий каждого типа x 1, x 2 и x 3 надо выпустить для получения максимального объема выпуска в денежном выражении, если цена изделий составляет по калькуляции 4, 3 и 2 рубля. ¿ _13. Задача сводится к вычислению максимума функции f (x 1, x 2, x 3)=4× x 1+3× x 2+2× x 3. 1) Зададим функцию, а также начальные приближения для x 1, x 2, x 3 равные 1. 2) Откроем блок Given. 3) Так как каждого изделия нужно сделать не менее 20 штук, то зададим ограничения вида:
4) Из условий задачи запишем еще два ограничения:
5) Из условия задачи известно всего деталей должно быть 100 штук, т.е.
6) Зададим некоторый вектор, например, R, как функцию максимума
7) Вывести значение этого вектора на экран.
Решение дифференциальных уравнений Напомним, что обыкновенным дифференциальным уравнением n -го порядка называется уравнение вида Дифференциальное уравнение первого порядка имеет вид MathCAD предоставляет широкие возможности для решения обыкновенных дифференциальных уравнений ОДУ (в такое уравнение входят производные только по одной переменной). Поскольку решение дифференциальных уравнений состоит в интегрировании, чтобы обеспечить однозначность решения, необходимо задавать дополнительные условия для определения постоянных интегрирования. & MathCAD решает ОДУ двух типов: · Задачи Коши – ОДУ с начальными условиями (задаются значения функции и ее производных в начальной точке интервала интегрирования); · Краевые задачи – ОДУ с граничными условиями (задаются значения функции и ее производных в начале и в конце интервала интегрирования). Начиная с версии MathCAD 2000, для решения дифференциальных уравнений и их систем появилась функция Odesolve. Она позволяет записывать уравнение в блоке решения в привычном виде, как обычно записывают уравнение на листе бумаги. Функция Odesolve возвращает решение дифференциального уравнения в виде функции. & Перед обращением к функции Odesolve необходимо записать слово Given. После этого записывается само дифференциальное уравнение и начальные или граничные условия к нему (или система дифференциальных уравнений и условия к ней). Далее идет сама функция Odesolve(x, xk, n), где x – имя переменной, относительно которой решается уравнение, xk – конец интервала интегрирования (начало интервала интегрирования указывается в начальных условиях), n – необязательный внутренний параметр, определяющий число шагов интегрирования, за которые должно быть найдено решение дифференциального уравнения. Чем больше n, тем с большей точностью будет решено уравнение, тем больше будет время решения. Задача_14. Решить дифференциальное уравнение ¿ _14. 1) Записать ключевое слово Given. 2) Записать уравнение
3) Задать начальные условия:
4) Задать функцию y = Odesolve(x, 5) и переменную x
5) Построить график функции y (x). Задача_15. Найти функцию & В качестве еще одного примера для решения обыкновенного дифференциального уравнения рассмотрим функцию rkfixed (y, x 1,x2, k, D). В отличие от рассмотренной выше функции Odesolve, она возвращает матрицу решений методом Рунге-Кутт
|
||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 183; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.249.119 (0.01 с.) |

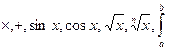 .
.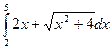 ; б)
; б) 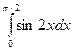 ; в)
; в) 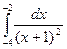 .
.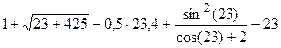 . Необходимо помнить о различиях между имеющимися математическими формулами и правилами, существующими в среде MathCAD: для разделения целой и дробной части используется точка; для возведения функции в степень, выражение функции берется в скобки, например,
. Необходимо помнить о различиях между имеющимися математическими формулами и правилами, существующими в среде MathCAD: для разделения целой и дробной части используется точка; для возведения функции в степень, выражение функции берется в скобки, например, 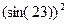 .
.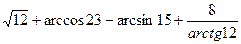 ; б)
; б) 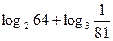 ; в)
; в) 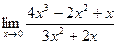 .
.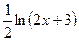 при x =3.
при x =3.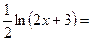 .
.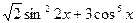 при
при 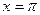 ;
;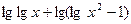 при
при  ; в)
; в) 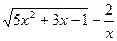 при
при 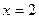 .
.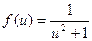 на указанном промежутке изменения аргумента.
на указанном промежутке изменения аргумента.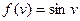 на указанном промежутке. Используя полосу прокрутки просмотреть полученные значения функции.
на указанном промежутке. Используя полосу прокрутки просмотреть полученные значения функции. .
.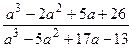 ; б)
; б) 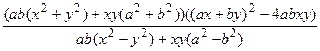
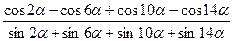
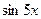 .
.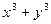 ; б)
; б) 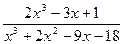 ; в)
; в) 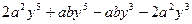 ; г)
; г) 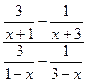
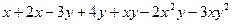 ; б)
; б) 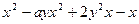 .
.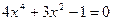 .
.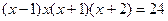 ;
;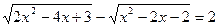 ; в)
; в) 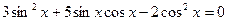 ; г)
; г) 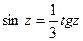
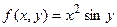 .
.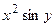 .
.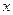 .
.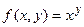 ; б)
; б) 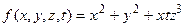 .
. .
. .
.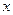 .
.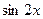 и
и 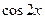 .
.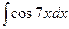 ; б)
; б) 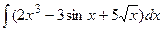 ; в)
; в) 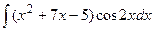 .
.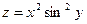 ;
; 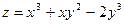 ; 2)
; 2) 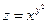 ;
; 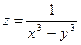 .
.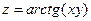 ;
; 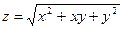 ; 4)
; 4) 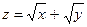 ;
; 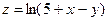 ;
; 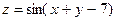 ;
; 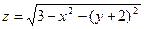 ; 6)
; 6) 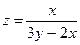 ;
; 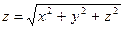 ;
;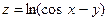 ;
; 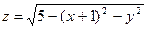 ; 8)
; 8) 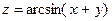 ;
; 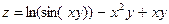 ;
;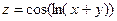 ;
; 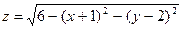 ; 10)
; 10) 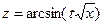 ;
; 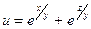 ;
;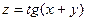 ;
; 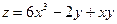 ; 12)
; 12) 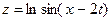 ;
; 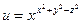 .
. 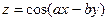 ;
; 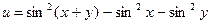 .
.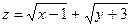 ;
;  .
. ;
; 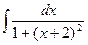 ;
; 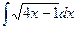 ;
; 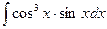 ;
; 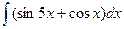 ;
; 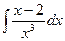 ;
; 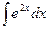 ;
; 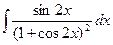 ;
; ;
; 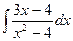 ;
; 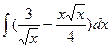 ;
; 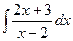 ;
;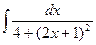 ;
; 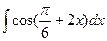 ;
; 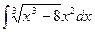 ;
; 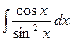 ;
; 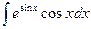 ;
; 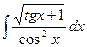 ;
; 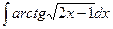 ;
; 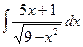 ;
;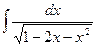 ;
; 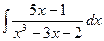 ;
; 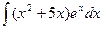 ;
; 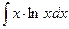 ;
;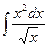 ;
; 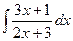 ;
; 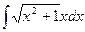 ;
; 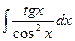 ;
;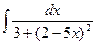 ;
; 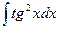 ;
; 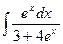 ;
; 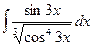 ;
;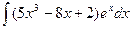 ;
; 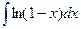 ;
; 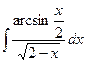 ;
; 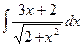 ;
;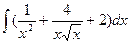 ;
; 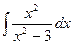 ;
; 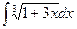 ;
; 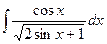 ;
; 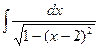 ;
; 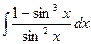 ;
; 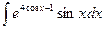 ;
; 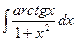 ;
;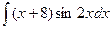 ;
; 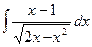 ;
; 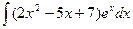 ;
; 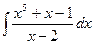 ;
;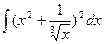 ;
; 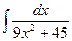 ;
; 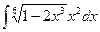 ;
; 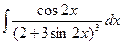 ;
; 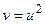 и прямой
и прямой  .
.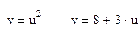
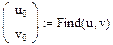
 ; б)
; б) 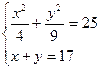 ; в)
; в) 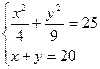 ; г)
; г) 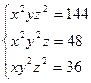
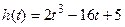 . Найти значения функции в этих точках. Постройте график данной функции.
. Найти значения функции в этих точках. Постройте график данной функции.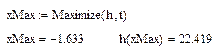
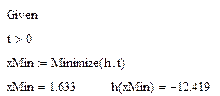
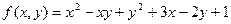 и найти значение функции
и найти значение функции 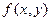 в точке минимума.
в точке минимума.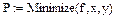
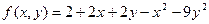 и найти значение функции
и найти значение функции 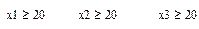
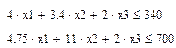

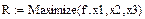
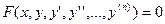 , где
, где 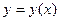 - искомая функция. Любая функция
- искомая функция. Любая функция 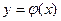 , обращающая данное уравнение в тождество, называется решением этого уравнения, а график этой функции – интегральной кривой.
, обращающая данное уравнение в тождество, называется решением этого уравнения, а график этой функции – интегральной кривой.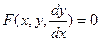 . Решив это уравнение относительно
. Решив это уравнение относительно 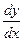 , получим
, получим 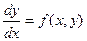 . Как известно из курса математического анализа, последнее уравнение определяет тангенс угла наклона интегральной кривой в точке
. Как известно из курса математического анализа, последнее уравнение определяет тангенс угла наклона интегральной кривой в точке 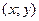 .
.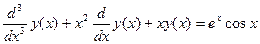 . С начальными условиями
. С начальными условиями 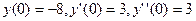 .
.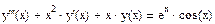 (символ «апостроф» для обозначения производной – Ctrl+F7).
(символ «апостроф» для обозначения производной – Ctrl+F7).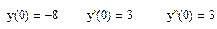
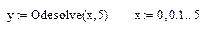
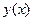 , удовлетворяющую дифференциальному уравнению
, удовлетворяющую дифференциальному уравнению 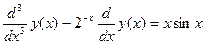 . С начальными условиями
. С начальными условиями 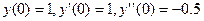 . Конец интервала интегрирования – 7. Построить график найденной функции.
. Конец интервала интегрирования – 7. Построить график найденной функции.


