Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные типы двумерных графиковСодержание книги
Поиск на нашем сайте
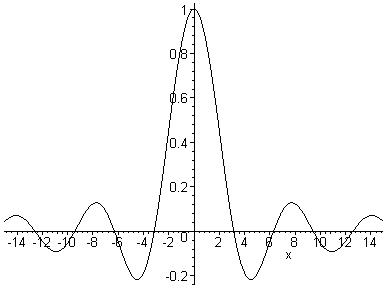
При построении графика одной функции она записывается в явном виде на месте параметра Построение простейших графиков в декартовой системе координат > plot(sin(x)/x,x=-15..15, color=black);
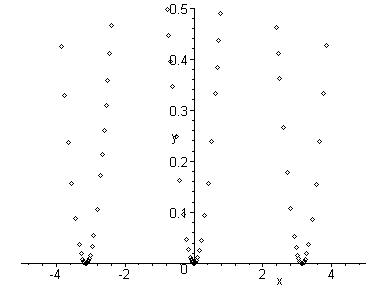
> plot(sin(x)^2,x=-5..5,y=0..0.5,color=black,style=point);
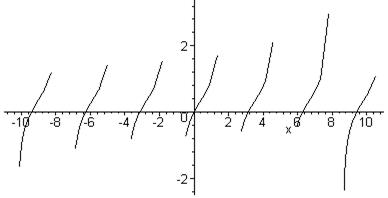
Графики функций с разрывами Среди аргументов функции plot есть параметрdiscont. Если задать его значение true, то качество графика улучшится. > plot(ln(1+tan(x)),x=-11..11,color=black);
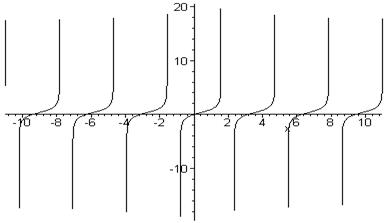
> plot(ln(1+tan(x)),x=-11..11,discont=true,color=black);
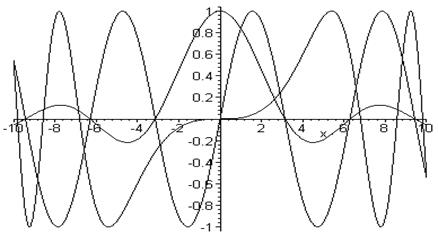
Графики нескольких функций на одном рисунке Важное значение имеет возможность построения на одном рисунке графиков нескольких функций. В простейшем случае для построения таких графиков достаточно перечислить нужные функции и установить для них общие интервалы изменения. Построение графиков трёх функций линиями одного типа > plot([sin(x),sin(x)/x,sin(x^3/100)],x=-10..10, color=black);
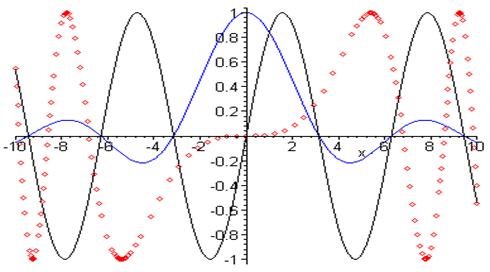
Построение графиков трёх функций линиями трёх цветов и трёх стилей > plot([sin(x),sin(x)/x,sin(x^3/100)],x=-10..10, color=[black,blue,red],style=[line,line,point]);
Построение графика функции > f(x):= sin(x)/x;
> plot([f(x),convert(series(f(x),x,15),polynom)],x=-10..10,y=-0.3..1,color=[black,blue],style=[line,point]);
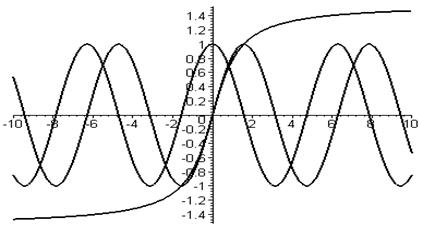
Построение графиков функций, заданных своими именами > plot([arctan,sin,cos],color=black,thickness=2);
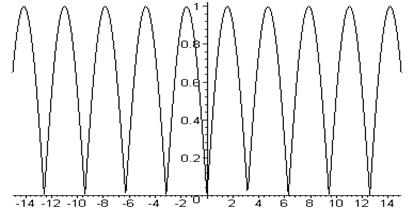
Построение графиков функций, заданных процедурами > w:=proc(x) if sin(x)>0 then sin(x) else -sin(x)fi end;
> plot(w,-15..15,color=black);
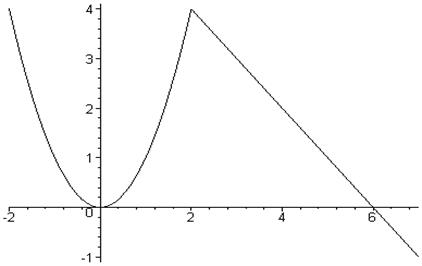
> z:=proc(x) if x>2 then 6-x else x^2 fi end;
> plot(z,-2..7,color=black);
Здесь в функции plot указывается имя процедуры без списка её параметров. Графики функций, заданных параметрически В ряде случаев для задания функциональных зависимостей используются заданные параметрически уравнения, например > plot([f1(t),f2(t),t=tmin..tmax],h,v,p); Если функции
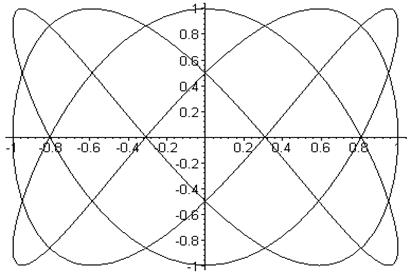
> plot([sin(3*t),cos(5*t),t=0..2*3.14],color=black);
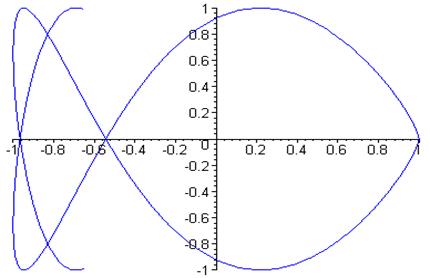
> plot([cos(x^2),sin(x^3),x=-2..2],-1..1,-1..1,color=blue);
Задание диапазонов для изменений h v, а также параметров p не обязательно. Но при использовании они позволяют получить вид графика, удовлетворяющий всем требованиям пользователя.
|
|||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 136; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.117.244 (0.009 с.) |

 .
.
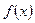 (сплошная чёрная линия и её полиномиальной аппроксимации (синие ромбы)
(сплошная чёрная линия и её полиномиальной аппроксимации (синие ромбы)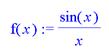
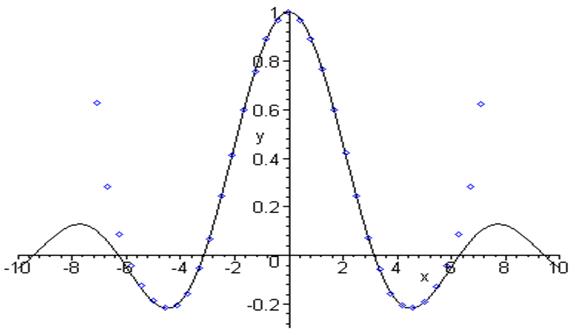


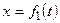 и
и 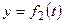 при изменении переменной е в некоторых пределах. Точки
при изменении переменной е в некоторых пределах. Точки 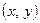 наносятся на график в декартовой системе координат и соединяются отрезками прямых. Для этого используется функция plot в следующей форме.
наносятся на график в декартовой системе координат и соединяются отрезками прямых. Для этого используется функция plot в следующей форме.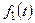 и
и 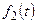 содержат периодические функции (например, тригонометрические), то для получения замкнутых фигур диапазон изменения переменной
содержат периодические функции (например, тригонометрические), то для получения замкнутых фигур диапазон изменения переменной 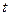 обычно задаётся равным 0..2*PI или –PI..PI. К примеру, если задать в качестве функций
обычно задаётся равным 0..2*PI или –PI..PI. К примеру, если задать в качестве функций 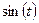 и
и 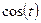 , то будет получен графику окружности.
, то будет получен графику окружности.