
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выбор образующего многочлена по заданному объему кода и заданной корректирующей способности.Содержание книги
Поиск на нашем сайте
По заданному объему кода однозначно определяется число информационных разрядов k. Далее необходимо найти наименьшее n, обеспечивающее обнаружение или исправление ошибок заданной кратности. В случае циклического кода эта проблема сводится к нахождению нужного многочлена g (x). Обнаружение одиночных ошибок. Любая принятая по каналу связи кодовая комбинация h (x), возможно содержащая ошибку, может быть представлена в виде суммы по модулю два неискаженной комбинации кода f (x) и вектора ошибки ξ (x):
При делении h (x) на образующий многочлен g (x) остаток, указывающий на наличие ошибки, обнаруживается только в том случае, если многочлен, соответствующий вектору ошибки, не делится на g (x): f (x) - неискаженная комбинация кода и, следовательно, на g (x) делится без остатка. Вектор одиночной ошибки имеет единицу в искаженном разряде и нули во всех остальных разрядах. Ему соответствует многочлен ξ (x) = х i. Последний не должен делиться на g (x). Среди неприводимых многочленов, входящих в разложении х n +1, многочленом наименьшей степени, удовлетворяющим указанному условию, является x +1. Остаток от деления любого многочлена на x +1 представляет собой многочлен нулевой степени и может принимать только два значения: 0 или 1. Все кольцо в данном случае состоит из идеала, содержащего многочлены с четным числом членов, и одного класса вычетов, соответствующего единственному остатку, равному 1. Таким образом, при любом числе информационных разрядов необходим только один проверочный разряд. Значение символа этого разряда как раз и обеспечивает четность числа единиц в любой разрешенной кодовой комбинации, а следовательно, и делимость ее на х +1. Полученный циклический код с проверкой на четность способен обнаруживать не только одиночные ошибки в отдельных разрядах, но и ошибки в любом нечетном числе разрядов. Исправление одиночных или обнаружение двойных ошибок. Прежде чем исправить одиночную ошибку в принятой комбинации из n разрядов, необходимо определить, какой из разрядов был искажен. Это можно сделать только в том случае, если каждой одиночной ошибке в определенном разряде соответствуют свой класс вычетов и свой опознаватель. Так как в циклическом коде опознавателями ошибок являются остатки от деления многочленов ошибок на образующий многочлен кода g (x), то g (x) должно обеспечить требуемое число различных остатков при делении векторов ошибок с единицей в искаженном разряде. Как отмечалось, наибольшее число остатков дает неприводимый многочлен. При степени многочлена r = n - k он может дать 2 n - k -1 ненулевых остатков (нулевой остаток является опознавателем безошибочной передачи). Следовательно, необходимым условием исправления любой одиночной ошибки является выполнение неравенства
где
и общее число символов в кодовой комбинации. Наибольшие значения k и n для различных m можно найти, пользуясь табл. 4. Как указывалось, образующий многочлен g (x) должен быть делителем двучлена х n +1. Доказано, что любой двучлен типа Таблица 4
Пользуясь этим свойством, а также имеющимися таблицами многочленов, неприводимых при двоичных коэффициентах, выбрать образующий многочлен при известных n и k несложно. Определив образующий многочлен, необходимо убедиться в том, что он обеспечивает заданное число остатков. Пример 7. Выберем образующий многочлен для случая n =15 и k =4. Двучлен x 15+1 можно записать в виде произведения всех неприводимых многочленов, степени которых являются делителями числа 4. Последнее делится на 1, 2, 4. В таблице неприводимых многочленов находим один многочлен первой степени, а именно х +1, один многочлен второй степени х 2+ х +1 и три многочлена четвертой степени: х 4+ x +1, х 4+ х 3+1, х 4+ х 3+ х +1. Перемножив все многочлены, убедимся в справедливости соотношения (х +1)(х 2+ х +1)(х 4+ х +1)(х 4+ х 3+l)(x 4+ x 3+ + x 2+ x +1)= x 12+1. Один из сомножителей четвертой степени может быть принят за образующий многочлен кода. Возьмем, например, многочлен х 4+ х 3+1, или в виде двоичной последовательности 11001. Чтобы убедиться, что каждому вектору ошибки соответствует отличный от других остаток, необходимо поделить каждый из этих векторов на 11001. Векторы ошибок младших разрядов имеют вид: 00...0001, 00...0010, 00...0100, 00...1000. Степени соответствующих им многочленов меньше степени образующего многочлена g (x). Поэтому они сами являются остатками при нулевой целой части. Остаток, соответствующий вектору ошибки в следующем старшем разряде, получаем при делении 00...10000 на 11001, т.е.
Аналогично могут быть найдены и остальные остатки. Однако их можно получить проще, деля на g (x) комбинацию в виде единицы с рядом нулей и выписывая все промежуточные остатки:
При последующем делении остатки повторяются. Таким образом, мы убедились в том, что число различных остатков при выбранном g (x) равно n =15, и, следовательно, код, образованный таким g (x), способен исправить любую одиночную ошибку. С тем же успехом за образующий многочлен кода мог быть принят и многочлен х 4+ x +1. При этом был бы получен код, эквивалентный выбранному. Однако использовать для тех же целей многочлен x 4+ х 3+ х 2+ x +1 нельзя. При проверке числа различных остатков обнаруживается, что их у него не 15, а только 5 Действительно,
Это объясняется тем, что многочлен x 4+ х 3+ х 2+ x +1 входит в разложение не только двучлена x 15+1, но и двучлена х 5+1. Из приведенного примера следует, что в качестве образующего следует выбирать такой неприводимый многочлен g (x) (или произведение таких многочленов), который, являясь делителем двучлена х n +1, не входит в разложение ни одного двучлена типа xr +1, степень которого r меньше n. В этом случае говорят, что многочлен q (x) принадлежит показателю степени n. В табл. 5 приведены основные характеристики некоторых кодов, способных исправлять одиночные ошибки или обнаруживать все одиночные и двойные ошибки. Таблица 5
Это циклические коды Хэмминга для исправления одной ошибки, в которых в отличие от групповых кодов Хэмминга все проверочные разряды размещаются в конце кодовой комбинации. Обнаружение ошибок кратности три и ниже. Образующие многочлены кодов, способных обнаруживать одиночные, двойные и тройные ошибки, можно определить, базируясь на следующем указании Хэмминга. Если известен образующий многочлен p (x r) кода длины n, позволяющего обнаруживать ошибки некоторой кратности z то образующий многочлен g (x) кода, способного обнаруживать ошибки следующей кратности (z +1), может быть получен умножением многочлена р (х r) на многочлен x +1, что соответствует введению дополнительной проверки на четность. При этом число символов в комбинациях кода за счет добавления еще одного проверочного символа увеличивается до n + 1. В табл. 6 приведены основные характеристики некоторых кодов, способных обнаруживать ошибки кратности три и менее. Таблица 6
Обнаружение и исправление независимых ошибок произвольной кратности. Важнейшим классом кодов, используемых в каналах, где ошибки в последовательностях символов возникают независимо, являются коды Боуза-Чоудхури-Хоквингема. Доказано, что для любых целых положительных чисел r и s < n /2 существует двоичный код этого класса длины n =2 r -1 с числом проверочных символов не более r s, который способен обнаруживать ошибки кратности 2 s или исправлять ошибки кратности s. Для произвольного линейного блокового (n, k)-кода, рассчитанного на исправление пакетов ошибок длины b или менее, основным соотношением, устанавливающим связь корректирующей способности с числом избыточных символов, является граница Рейджера: При исправлении линейным кодом пакетов длины b или менее с одновременным обнаружением пакетов длины l≥ b или менее требуется по крайней мере b + l проверочных символов. Из циклических кодов, предназначенных для исправления пакетов ошибок, широко известны коды Бартона, Файра и Рида-Соломона. Первые две разновидности кодов служат для исправления одного пакета ошибок в блоке. Коды Рида-Соломона способны исправлять несколько пачек ошибок.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 324; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.2 (0.006 с.) |

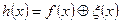 . (3)
. (3)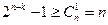 , (4)
, (4)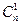 - общее число разновидностей одиночных ошибок в кодовой комбинации из n символов; отсюда находим степень образующего многочлена кода
- общее число разновидностей одиночных ошибок в кодовой комбинации из n символов; отсюда находим степень образующего многочлена кода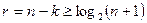 (5)
(5)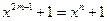 может быть представлен произведением всех неприводимых многочленов, степени которых являются делителями числа r (от 1 до r включительно). Следовательно, для любого m существует по крайней мере один неприводимый многочлен степени r, входящий сомножителем в разложение двучлена х n +1.
может быть представлен произведением всех неприводимых многочленов, степени которых являются делителями числа r (от 1 до r включительно). Следовательно, для любого m существует по крайней мере один неприводимый многочлен степени r, входящий сомножителем в разложение двучлена х n +1.


 (6)
(6)


