
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие принципы использования избыточности.Содержание книги Поиск на нашем сайте
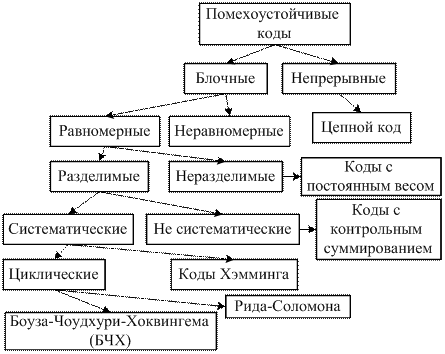
Теория помехоустойчивого кодирования базируется на результатах исследований, проведенных Шенноном и сформулированных им в виде теоремы: 1. При любой производительности источника сообщений, меньшей, чем пропускная способность канала, существует такой способ кодирования, который позволяет обеспечить передачу всей информации, создаваемой источником сообщений, со сколь угодно малой вероятностью ошибки. 2. Не существует способа кодирования, позволяющего вести передачу информации со сколь угодно малой вероятностью ошибки, если производительность источника сообщений больше пропускной способности канала. Теорема устанавливает теоретический предел возможной эффективности системы при достоверной передаче информации. Ею опровергнуто казавшееся интуитивно правильным представление о том, что достижение сколь угодно малой вероятности ошибки в случае передачи информации по каналу с помехами возможно лишь при введении бесконечно большой избыточности, т. е. при уменьшении скорости передачи до нуля. Из теоремы следует, что помехи в канале не накладывают ограничений на точность передачи. Ограничение накладывается только на скорость передачи, при которой может быть достигнута сколь угодно высокая достоверность передачи. Теорема неконструктивна в том смысле, что в ней не затрагивается вопрос о путях построения кодов, обеспечивающих указанную идеальную передачу. Однако, обосновав принципиальную возможность такого кодирования, она мобилизовала усилия ученых на разработку конкретных кодов. Следует отметить, что при любой конечной скорости передачи информации вплоть до пропускной способности сколь угодно малая вероятность ошибки достигается лишь при безграничном увеличении длительности кодируемых последовательностей знаков. Таким образом, безошибочная передача при наличии помех возможна лишь теоретически. Помехоустойчивые коды используются как для исправления ошибок (корректирующие коды), так и для их обнаружения. Блочными кодами являются коды, в которых каждому сообщению ставится в однозначное соответствие блок из n символов. В соответствии с этим блочные коды делятся на равномерные и неравномерные. Основное внимание при разработке кодов уделено равномерным кодам.
Непрерывные коды представляют непрерывную последовательность информационных и проверочных разрядов. К непрерывным кодам относится цепной код. Равномерные блочные коды бывают разделимые и неразделимые. Под разделимым понимают код, в котором разряды могут быть принципиально разделены на проверочные и информационные. При этом места проверочных и информационных разрядов в кодовой комбинации вполне определены. В неразделимых кодах деление на информационные и проверочные разряды отсутствует. Примером таких кодов являются коды с постоянным весом. Разделимые коды подразделяются на систематические и несистематические. Систематическими кодами называют такие, у которых сумма по модулю 2 двух разрешенных комбинаций кода дает комбинацию того же кода. Примерами систематических кодов являются циклические коды и коды Хэмминга. Для систематического кода применяется обозначение (n, k) - код, где n - число всех разрядов в кодовой комбинации, k - число информационных разрядов.
Несистематические коды указанным выше свойством не обладают. Примером несистематического ода является код с контрольным суммированием, в котором проверочные разряды представляют запись суммы единиц в кодовой комбинации. Все перечисленные выше коды, в принципе, могут быть использованы как в качестве обнаруживающих, так и в качестве исправляющих ошибки кодов. Однако на практике одни коды находят наибольшее применение как обнаруживающие, другие - как коды с исправлением ошибок. Например, цепной код используется как код с исправлением ошибок.
Способность кода обнаруживать и исправлять ошибки обусловлена наличием избыточных символов. На вход кодирующего устройства поступает последовательность из k информационных двоичных символов. На выходе ей соответствует последовательность из п двоичных символов, причем n > k.
Остальные 2 n -2 k возможных выходных последовательностей для передачи не используются. Назовем их запрещенными комбинациями.
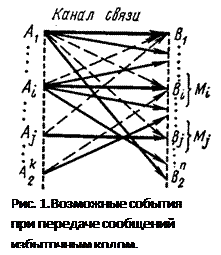
Искажение информации в процессе передачи сводится к тому, что некоторые из переданных символов заменяются другими - неверными. Так как каждая из 2 k разрешенных комбинаций в результате действия помех может трансформироваться в любую другую, то всего имеется 2 k ·2 n возможных случаев передачи (рис. 1). В это число входят: Ø 2 k случаев безошибочной передачи (на рис.1 обозначены жирными линиями); Ø 2 k (2 k -1) случаев перехода в другие разрешенные комбинации, что соответствует необнаруживаемым ошибкам (на рис.1 обозначены пунктирными линиями); Ø 2 k (2 n -2 k) случаев перехода в неразрешенные комбинации, которые могут быть обнаружены (на рис. 1 обозначены тонкими сплошными линиями). Следовательно, часть обнаруживаемых ошибочных кодовых комбинаций от общего числа возможных случаев передачи составляет:
Рассмотрим случай исправления ошибок. Любой метод декодирования можно рассматривать как правило разбиения всего множества запрещенных кодовых комбинаций на 2 k непересекающихся подмножеств Mi, каждое из которых ставится в соответствие одной из разрешенных комбинаций. При получении запрещенной комбинации, принадлежащей подмножеству Mi, принимают решение, что передавалась разрешенная комбинация Ai. Ошибка будет исправлена в тех случаях, когда полученная комбинация действительно образовалась из Ai т.е. 2 n -2 k случаях. Всего случаев перехода в неразрешенные комбинации 2 k (2 n -2 k). Таким образом, при наличии избыточности любой код способен исправлять ошибки. Отношение числа исправляемых кодом ошибочных кодовых комбинаций к числу обнаруживаемых ошибочных комбинаций равно
Способ разбиения на подмножества зависит от того, какие ошибки должны исправляться данным конкретным кодом. Большинство разработанных до настоящего времени кодов предназначено для корректирования взаимно независимых ошибок определенной кратности и пачек (пакетов) ошибок. Взаимно независимыми ошибками будем называть такие искажения в передаваемой последовательности символов, при которых вероятность появления любой комбинации искаженных символов зависит только от числа искаженных символов r и вероятности искажения одного символа р. Кратностью ошибки называют количество искаженных символов в кодовой комбинации. При взаимно независимых ошибках вероятность искажения любых r символов в n -разрядной кодовой комбинации
Если учесть, что p <<l, то в этом случае наиболее вероятны ошибки низшей кратности. Их и следует обнаруживать и исправлять в первую очередь.
|
||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 333; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.149.44 (0.009 с.) |

 Всего может быть 2 k различных входных и 2 n различных выходных последовательностей. Из общего числа 2 n выходных последовательностей только 2 k последовательностей соответствуют входным. Назовем их разрешенными кодовыми комбинациями.
Всего может быть 2 k различных входных и 2 n различных выходных последовательностей. Из общего числа 2 n выходных последовательностей только 2 k последовательностей соответствуют входным. Назовем их разрешенными кодовыми комбинациями. . (1)
. (1)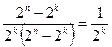 . (2)
. (2)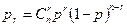 . (3)
. (3)


