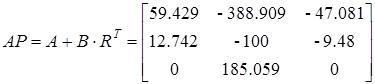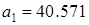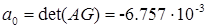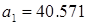Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Синтез САУ методом последовательной коррекции с подчиненным регулированием координатСодержание книги
Поиск на нашем сайте
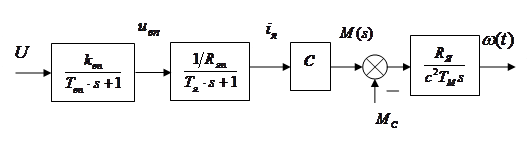
Основу метода последовательной коррекции с подчинённым регулированием координат составляют два принципа. Первый принцип – принцип подчинённого каскадного включения регуляторов отдельных координат состояния заключается в выборе замкнутых внутренних контуров регулирования, подчинённых общей задаче регулирования управляемой координаты. При этом выбор замкнутых внутренних контуров производится из условия формирования такой передаточной функции объекта управления в каждом контуре, при которой синтез последовательно включенных регуляторов контуров возможен в классе типовых линейных законов управления ограниченной сложности. Второй принцип – принцип последовательной компенсации средних и больших постоянных времени контуров регулирования основан на последовательной замене исходного разомкнутого контура регулирования последовательностью результирующих контуров с желаемыми передаточными функциями. Выбор разомкнутых контуров в виде последовательного соединения интегрирующего и апериодического звена с малой некомпенсируемой постоянной времени обеспечивает высокую точность (астатическое регулирование) и высокое быстродействие системы. В качестве внутренних регулируемых координат состояния при управлении в ВЭМС выбирают токи, напряжения и частоту питания и на выходе НПЭ, потокосцепления ЭМП, угловую скорость и момент на валу ЭМП, положение вала приводного механизма и др., что позволяет вводить независимые ограничения на эти координаты. Для начала необходимо упростить структурную схему системы "Вентильный преобразователь – машина постоянного тока", показанную на рисунке 10. Для этого пренебрегаем обратной связью в цепи с МПТ.
Рисунок 10
Для первого контура входным является напряжение на входе в ВП
Рисунок 11
Желаемая ПФ данного контура с обеспечением заданных показателей качества будет следующей:
Здесь а1 – параметр, влияющий на перерегулирование. Для обеспечения Для нахождения ПФ первого регулятора произведем следующие действия:
Данный регулятор – ПИ-регулятор. ПФ замкнутого контура
Для второго контура структурная схема выглядит так:
Рисунок 12
Желаемая ПФ второго разомкнутого контура (а2=2):
Тогда ПФ второго регулятора:
Здесь присутствует только пропорциональная часть:
Следовательно, второй регулятор – П-регулятор. Анализ синтезированной системы будем проводить по следующей структурной схеме, то есть с вновь введенной обратной связью:
Рисунок 13
Здесь:
Для составления ММ в пространстве состояний необходимо схему на рисунке 13 представить во временной области.
Рисунок 14
Уравнение ММ в пространстве состояний запишем по рисунку 14:
По данной ММ построены временные и частотные характеристики, оценены показатели качества в приложении 2.
Модальное управление
Модальное управление – это управление посредством динамической обратной связи с матрицей коэффициентов Необходимо обеспечить следующий желаемый спектр:
где
Исходная система имеет вид:
Произведем следующую последовательность действий: 1. Трансформация исходной системы к канонически управляемому базису с вычислением матрицы перехода. a. Матрица управляемости
Как было определено ранее, система управляема. b. Определяем характеристические полиномы
Спектр исходной системы:
Коэффициенты характеристического полинома:
Для желаемого спектра
Коэффициенты характеристического полинома:
c. Составляем сопровождающую матрицу полинома.
d. Вычисляем матрицу управляемости преобразованной системы.
e. Определяем матрицу перехода.
2. Расчёт параметров модального регулятора преобразованной системы.
3. Переход к исходному базису и расчёт коэффициентов модального регулятора.
4. Определение спектра синтезированной системы. В исходном базисе:
В каноническом базисе:
Коэффициенты характеристических полиномов синтезированной системы в исходном и в канонически управляемом базисе совпадают, что свидетельствует о правильности приведенных преобразований. В Приложении 3 построены временные и частотные характеристики синтезированной системы.
|
||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 84; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.144.162 (0.008 с.) |

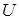 , а выходным – ток цепи якоря
, а выходным – ток цепи якоря 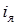 . Постоянная времени ВП является некомпенсируемой, так как она намного меньше остальных постоянных времени. Структурная схема будет выглядеть так:
. Постоянная времени ВП является некомпенсируемой, так как она намного меньше остальных постоянных времени. Структурная схема будет выглядеть так: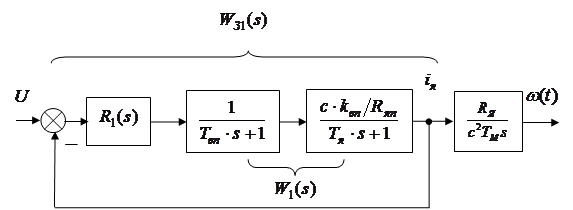

 этот параметр принимает значение 2.
этот параметр принимает значение 2.
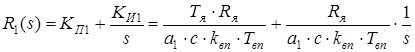
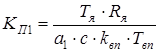 - пропорциональная часть;
- пропорциональная часть;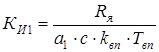 - интегрирующая часть.
- интегрирующая часть.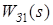 представляет собой колебательное звено и может быть аппроксимировано следующим образом:
представляет собой колебательное звено и может быть аппроксимировано следующим образом: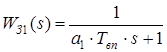 .
.
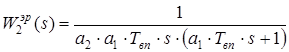 .
. .
.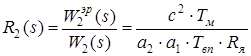
 .
.
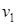 - выход с первого регулятора;
- выход с первого регулятора;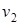 - напряжение на выходе вентильного преобразователя;
- напряжение на выходе вентильного преобразователя;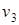 - ток якоря;
- ток якоря; - угловая скорость.
- угловая скорость.
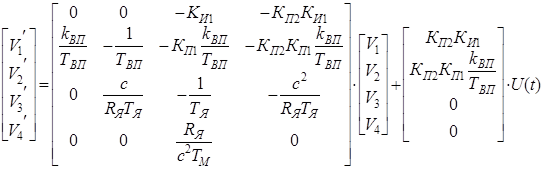
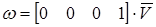
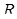 модами (собственными числами, корнями характеристического полинома) для достижения желаемых целей.
модами (собственными числами, корнями характеристического полинома) для достижения желаемых целей.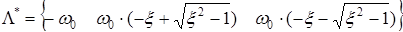 ,
,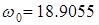 ,
, 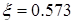 для обеспечения заданных показателей качества. Тогда:
для обеспечения заданных показателей качества. Тогда: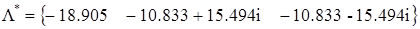
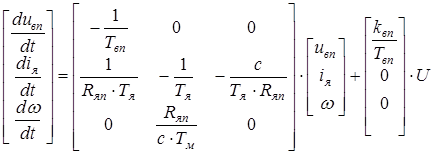 ,
,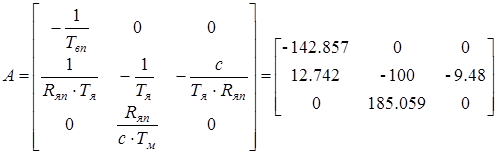 ,
,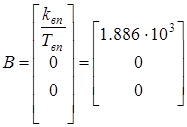 ,
,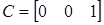 .
.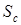 исходной системы (она была определена выше при определении устойчивости системы).
исходной системы (она была определена выше при определении устойчивости системы).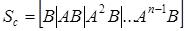
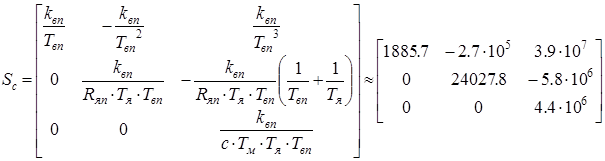
 и
и 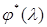 .
.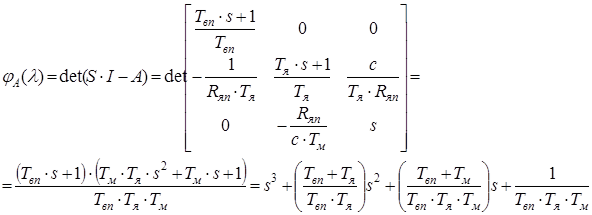
 ,
,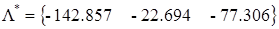 .
.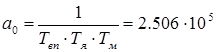 ,
, ,
, .
.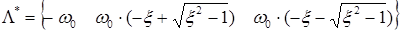 :
: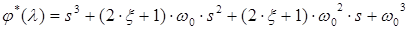
 ,
,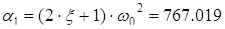 ,
, .
.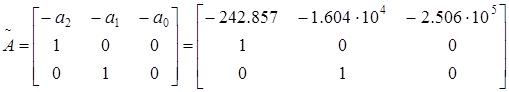 ,
,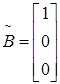 .
.
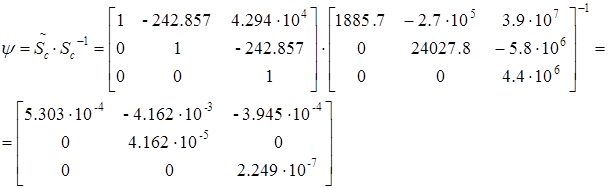
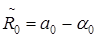 ,
,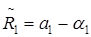 ,
,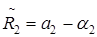 ,
,
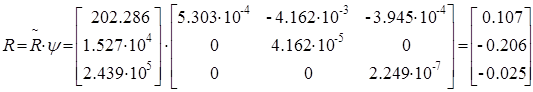 ,
,