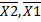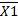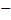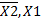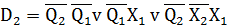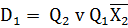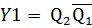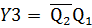Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Граф управляючого автомата Мура з кодами вершинСодержание книги
Поиск на нашем сайте
Рисунок 2.7.5 – Граф автомата Мура Обробка порядків PX+Y= 810 =10002 Форма запису результату з плаваючою комою Результат додавання Z=X+Y. Zпк = 1. 110011011110111 Pz = 810 =10002 Mz = 1100110111101112
Операція добування кореня Теоритичне обґрунтування операції обчислення квадратного кореня
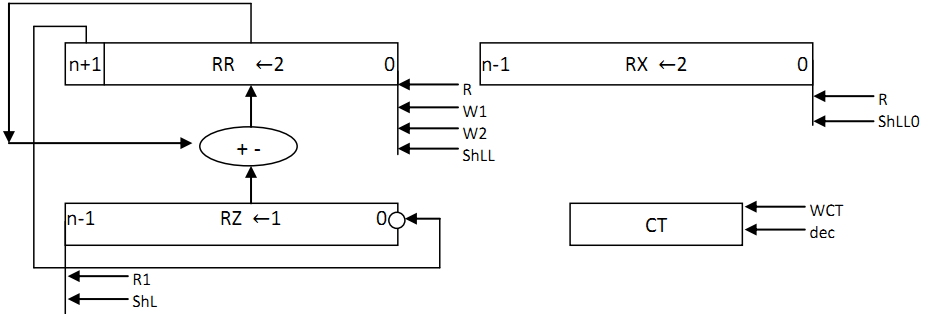
2.8.2 Операційна схема операції обчислення квадратного кореня Рисунок 2.8.1 –Операційна схем Змістовний мікроалгоритм
Рисунок 2.8.2 – Змістовний мікроалгоритм Таблиця станів регістрів Таблиця 2.8.1 – Таблиця станів регістрів
Функціональна схема операції обчислення квадратного кореня
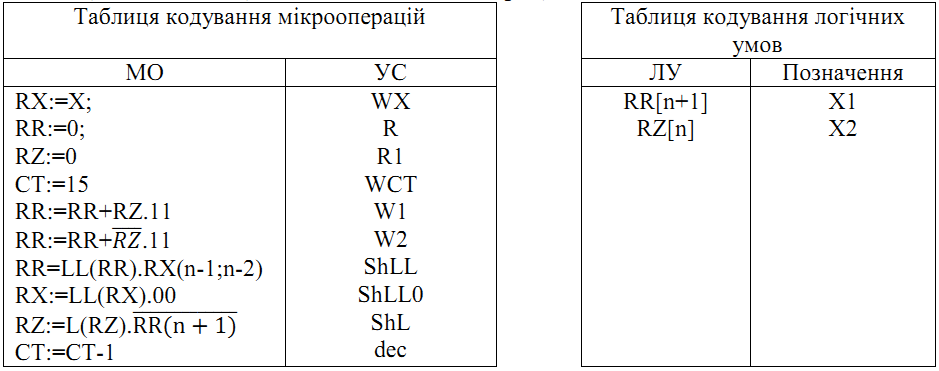
Рисунок 2.8.3 – Функціональна схема 2.8.6 Закодований мікроалгоритм Таблиця 2.8.2 – Таблиця кодування
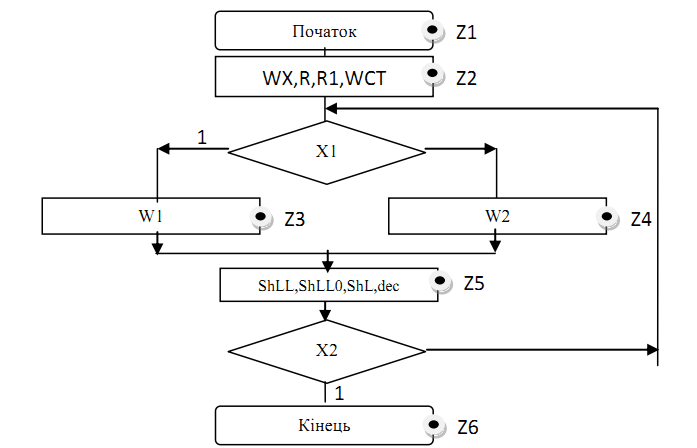
Рисунок 2.8.4 – Закодований мікроалгоритм Граф управляючого автомата Мура з кодами вершин
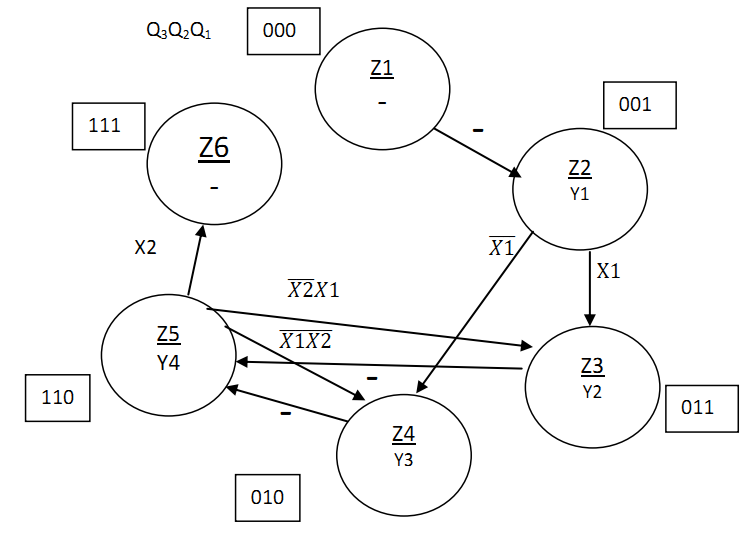
Рисунок 2.8.5 – Граф управляючого автомата Мура
Обробка порядків
В моєму випадку Запис результату Отримали результат Z = 110110000111100; Результат нормалізований, готовий до запису у мантису:
Завдання 3 x3 x2 x1 +1 = 1002 = 410. Синтез управляючого автомату Мура на D-тригерах для операції множення четвертим способом Таблиця кодування сигналів Таблиця 3.1 – Таблиця кодування сигналів
3.2 Мікроалгоритм в термінах управляючого автомата
Рисунок 3.1 – Закодований мікроалгоритм
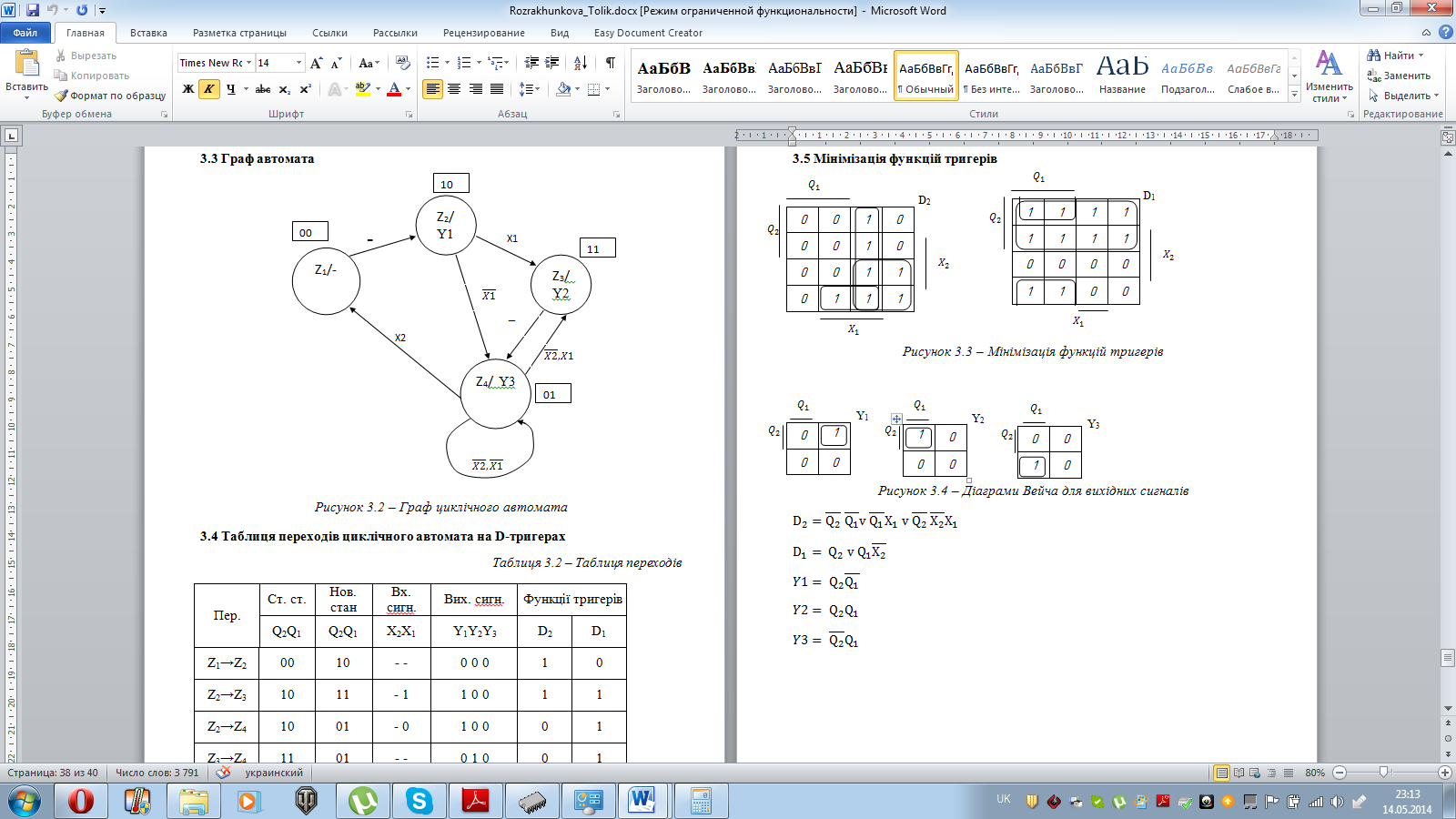
Рисунок 3.2 – Граф циклічного автомата Таблиця переходів циклічного автомата на D-тригерах Таблиця 3.2 – Таблиця переходів
Мінімізація функцій тригерів
Функціональна схема автомата
Рисунок 3.5 - Функціональна схема в програмі AFDK Висновок У даній розрахунковій роботі було виконано операції з числами в двійковому коді з плаваючою комою, а саме: множення чотирма способами, ділення двома способами та додавання. Для операції множення другим способом було побудовано управляючий автомат Мура на D-тригерах і елементах булевого базису. Зроблено мінімізацію функцій тригерів і в середовищі AFDK побудована функціональна схема автомата. Під час виконання даної розрахункової роботи я повторив для себе матеріал курсу «Компютерна логіка - 1», а також закріпив знання з курсу «Компютерна логіка - 2». Було використано наступну літературу: 1) Жабін В.І., Жуков І.А., Клименко І.А.,Ткаченко В.В. Прикладна теорія цифрових автоматів: Навчальний посібник. – К.: Книжкове вид-во НАУ, 2009. – 360 с.
2) Конспект лекцій з курсу «Комп ’ ютерна логіка - 1» 3) Конспект лекцій з курсу «Комп ’ ютерна логіка - 2»
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 103; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.186.109 (0.012 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||




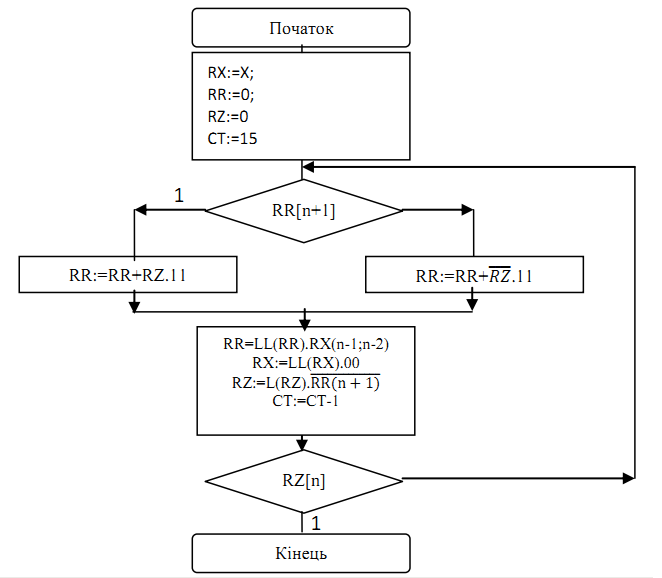
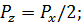
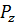 =4;
=4;