
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра обчислювальної технікиСодержание книги
Поиск на нашем сайте
ФАКУЛЬТЕТ ІНФОРМАТИКИ ТА ОБЧИСЛЮВАЛЬНОЇ ТЕХНІКИ Кафедра обчислювальної техніки
РОЗРАХУНКОВА РОБОТА
по курсу „Комп'ютерна арифметика” Виконав: Шепель Дмитро Група ІО-34, Факультет ІОТ, Залікова книжка № 3427 Номер технічного завдання 110101100011
_______________________ (підпис керівника)
Київ – 2014 р. Завдання 1. Числа 2. Виконати 8 операцій з числами 2.1 теоретичне обґрунтування способу; 2.1 операційну схему; 2.2 змістовний мікроалгоритм; 2.3 таблицю станів регістрів (лічильника), довжина яких забезпечує одержання 15 основних розрядів мантиси результату; 2.4 функціональну схему з відображенням управляючих сигналів; 2.5 закодований мікроалгоритм (мікрооперації замінюються управл. сигналами); 2.6 граф управляючого автомата Мура з кодами вершин; 2.7 обробку порядків (показати у довільній формі); 2.8 форму запису нормалізованого результату з плаваючою комою в пам’ять. Вказані пункти для операцій додавання виконати для етапу нормалізації результату з урахуванням можливого нулевого результату. Інші дії до етапу нормалізації результату можна проілюструвати у довільній формі. 3. Для операції з номером
Варіант завдання Перевести номер залікової книжки в двійкову систему. Записати два двійкових числа:
де 341810 Х2 = -10110111,0000111; Y2 = +10110,1110000111;
Виконання завдання Завдання №1 Xпк = 1. 10110111,0000111; Yпк = 0. 10110,1110000111 Представлення чисел у формі з плаваючою точкою з порядком і мантисою:
Х2:
Y2:
Представлення чисел у формі з плаваючою точкою з характеристикою і мантисою:
Для Х2: m = 8
Для Y2: m = 5
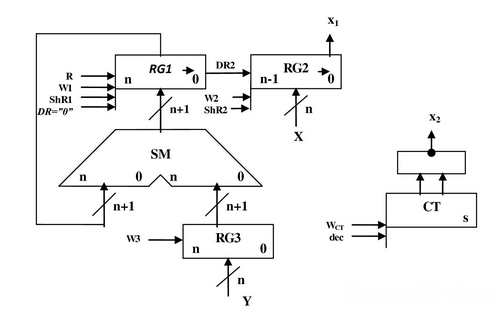
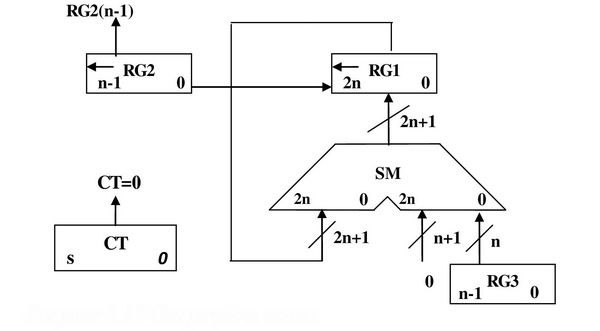
Завдання №2 Перший спосіб множення. 2.1.1 Теоретичне обґрунтування першого способу множення: Числа множаться у прямих кодах, знакові та основні розряди обробляються окремо. Для визначення знака добутку здійснюють підсумування по модулю 2 цифр, що розміщуються в знакових розрядах співмножників. Множення мантис першим способом здійснюється з молодших розрядів множника, сума часткових добутків зсувається вправо, а множене залишається нерухомим. Тоді добуток двох чисел представляється у вигляді: Z=YХ= = ((..((0+Y Z= 2.1.2 Операційна схема:
Рисунок 2.1.1- Операційна схема. 2.1.3 Змістовний мікроалгоритм:
Рисунок 2.1.2 - Змістовний мікроалгоритм виконання операції множення першим способом. 2.1.4 Таблиця станів регістрів: Таблиця 2.1.1-Таблиця станів регістрів для першого способу множення.
Функціональна схема:
Рисунок 2.1.3- Функціональна схема. Закодований мікроалгоритм
Рисунок 2.1.4-Закодований мікроалгоритм. Таблиця 2.1.2-Таблиця кодування операцій і логічних умов.
2.1.7 Граф управляючого автомата Мура з кодами вершин:
Рисунок 2.1.5-Граф автомата Мура 2.1.8 Обробка порядків: Порядок добутку буде дорівнювати сумі порядків множників з урахуванням знаку порядків:
Нормалізація результату: Отримали результат: 0100000101110010100000100110001 Знак мантиси: 1 Робимо зсув результату вліво, доки у першому розряді не буде одиниця, Порядок зменшуємо на 1: 100000101110010100000100110001; Запишемо нормалізований результат:
Другий спосіб множення. 2.2.1 Теоретичне обґрунтування другого способу множення: Числа множаться у прямих кодах, знакові та основні розряди обробляються окремо. Визначення знака добутку здійснюють підсумування по модулю 2 цифр, що розміщуються в знакових розрядах співмножників. Множення мантис другим способом здійснюється з молодших розрядів, множене зсувається вліво, а сума часткових добутків залишається нерухомою. Z=Y Z=((0+ Y Z=
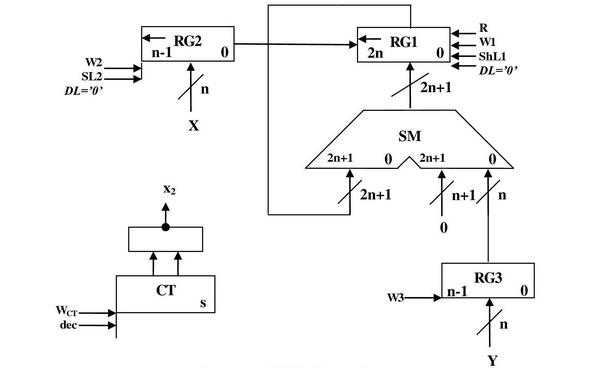
2.2.2 Операційна схема:
Рисунок 2.2.1- Операційна схема 2.2.3 Змістовний мікроалгоритм:
Рисунок 2.2.2 - Змістовний мікроалгоритм. 2.2.4 Таблиця станів регістрів: Таблиця 2.2.1-Таблиця станів регістрів.
2.2.5 Функціональна схема:
Рисунок 2.2.3- Функціональна схема. Закодований мікроалгоритм
Початок Z1
R,W2,W3 Z2
X1
W1 Z3
ShR, ShL Z4
X2
1
Кінець Z5
Таблиця 2.2.2-Таблиця кодування операцій і логічних умов.
2.2.7 Граф управляючого автомата Мура з кодами вершин: Рисунок 2.2.5 - Граф автомата Мура 2.2.8 Обробка порядків: Порядок добутку буде дорівнювати сумі порядків множників з урахуванням знаку порядків:
Нормалізація результату: Отримали результат: 100000101110010100000100110001 Знак мантиси: 1 Робимо здвиг результату вліво, доки у першому розряді не буде одиниця, Порядок зменшуємо на 1: 100000101110010100000100110001; Запишемо нормалізований результат:
Третій спосіб множення. 2.3.1Теоретичне обгрунтування третього способу множення: Числа множаться у прямих кодах, знакові та основні розряди обробляються окремо. Визначення знака добутку здійснюють підсумування по модулю 2 цифр, що розміщуються в знакових розрядах співмножників. Множення мантис третім способом здійснюється зі старших розрядів множника, сума часткових добутків і множник зсуваються вліво, а множене нерухоме.
Z=Y Z= Y Z=
2.3.2 Операційна схема:
Рисунок 2.3.1 - Операційна схема 2.3.3 Змістовний мікроалгоритм:
2.3.4 Таблиця станів регістрів: Таблиця 2.3.1- Таблиця станів регістрів
Функціональна схема:
Рисунок 2.3.3 - Функціональна схема. 2.3.6 Закодований мікроалгоритм: Таблиця 2.3.2-Таблиця кодування операцій і логічних умов.
Рисунок 2.3.4-Закодований мікроалгоритм. 2.3.7 Граф управляючого автомата Мура з кодами вершин:
Рисунок 2.3.5 - Граф автомата Мура 2.3.8 Обробка порядків: Порядок добутку буде дорівнювати сумі порядків множників з урахуванням знаку порядків:
Нормалізація результату: Отримали результат: 100000101110010100000100110001 Знак мантиси: 1 Робимо здвиг результату вліво, доки у першому розряді не буде одиниця, порядок зменшуємо на 1: 100000101110010100000100110001; Запишемо нормалізований результат:
Четвертий спосіб множення. 2.4.1Теоритичне обґрунтування четвертого способу множення: Числа множаться у прямих кодах, знакові та основні розряди обробляються окремо. Визначення знака добутку здійснюють підсумування по модулю 2 цифр, що розміщуються в знакових розрядах співмножників. Множення здійснюється зі старших розрядів множника, сума часткових добутків залишається нерухомою, множене зсувається праворуч, множник ліворуч.
2.4.2 Операційна схема:
Рисунок 2.4.1- Операційна схема 2.4.3 Змістовний мікроалгоритм:
2.4.4 Таблиця станів регістрів: Таблиця 2.4.1- Таблиця станів регістрів
2.4.5Функціональна схема:
Рисунок 2.4.3 - Функціональна схема. Закодований мікроалгоритм Таблиця 2.4.2-Таблиця кодування операцій і логічних умов.
Рисунок 2.4.4-Закодований мікроалгоритм. 2.4.7 Граф управляючого автомата Мура з кодами вершин: Рисунок 2.4.5 - Граф автомата Мура 2.4.8 Обробка порядків: Порядок добутку буде дорівнювати сумі порядків множників з урахуванням знаку порядків:
Нормалізація результату: Отримали результат: 100000101110010100000100110001 Знак мантиси: 1 Робимо здвиг результату вліво, доки у першому розряді не буде одиниця, Порядок понижаємо на 1: 100000101110010100000100110001; Запишемо нормалізований результат:
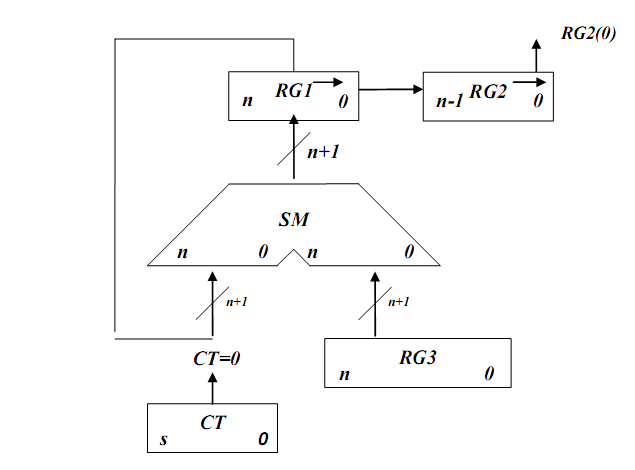
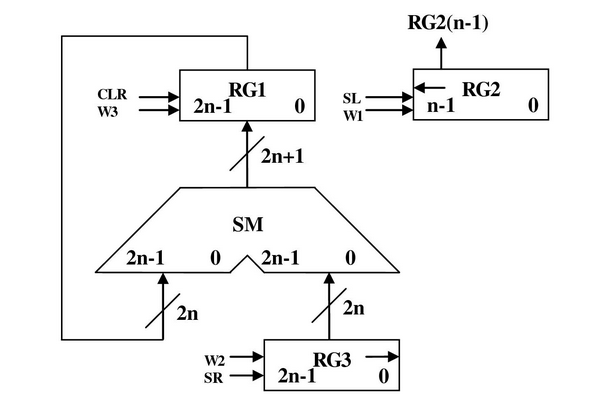
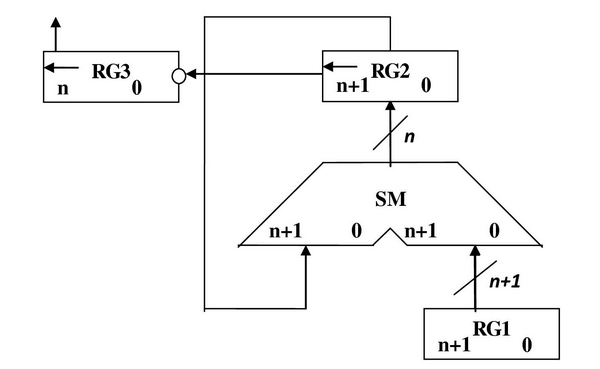
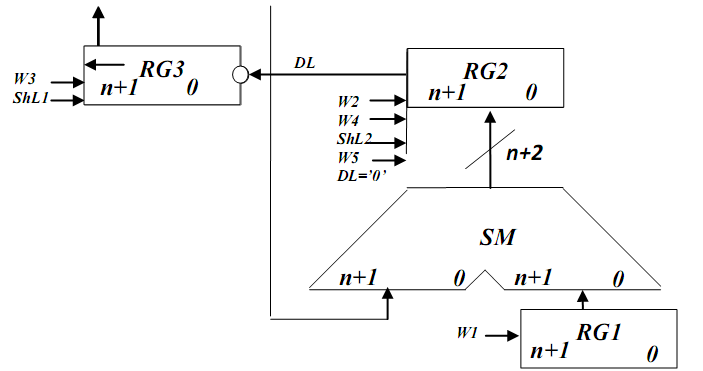
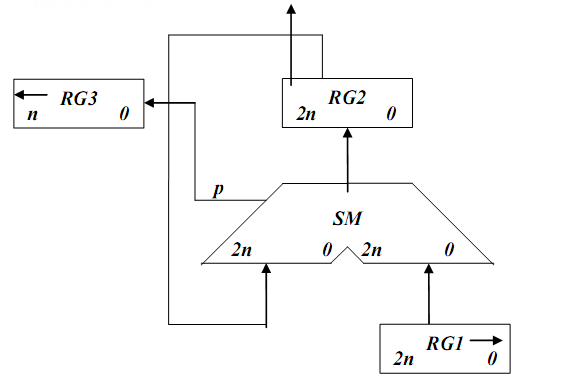
Першиий спосіб ділення. 2.5.1Теоритичне обґрунтування першого способу ділення: Нехай ділене Х і дільник Y є n-розрядними правильними дробами, поданими в прямому коді. В цьому випадку знакові й основні розряди операндів обробляються окремо. Знак результату визначається шляхом підсумовування по модулю 2 цифр, записаних в знакових розрядах. При реалізації ділення за першим методом здійснюється зсув вліво залишку при нерухомому дільнику. Черговий залишок формується в регістрі RG2 (у вихідному стані в цьому регістрі записаний Х). Виходи RG2 підключені до входів СМ безпосередньо, тобто ланцюги видачі коду з RG2 не потрібні. Час для підключення n+1 цифри частки визначається виразом t=(n+1)(tt+tc), де tt - тривалість виконання мікрооперації додавання-віднімання; tc - тривалість виконання мікрооперації зсуву. Операційна схема:
Рисунок 2.5.1- Операційна схема Змістовний мікроалгоритм:
Р и сунок 2.5.2-Змістовний мікроалгоритм
Таблиця станів регістрів:
2.5.5 Функціональна схема:
Рисунок 2.5.3 – Функціональна схема Закодований мікроалгоритм Таблиця 2.5.2-Таблиця кодування операцій і логічних умов.
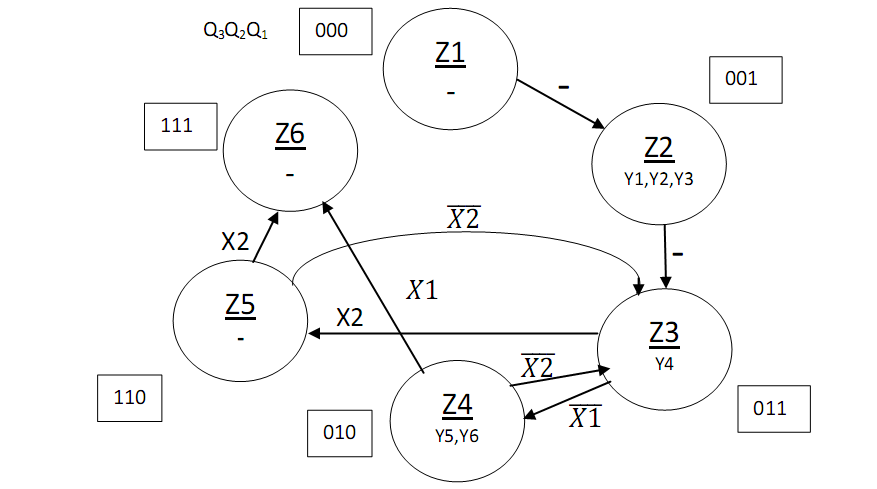
Рисунок 2.5.4-Закодований мікроалгоритм. 2.5.7 Граф управляючого автомата Мура з кодами вершин:
Рисунок 2.5.5 - Граф управляючого автомата. 2.5.8 Обробка порядків: Порядок частки буде дорівнювати: В моєму випадку 2.5.8 Нормалізація результату: Отримали результат: 1111010000001001 Знак мантиси: 1 Нормалізація мантиси не потрібна.
Другий спосіб ділення. 2.6.1Теоритичне обгрунтування другого способу ділення: Нехай ділене Х і дільник Y є n-розрядними правильними дробами, поданими в прямому коді. В цьому випадку знакові й основні розряди операндів обробляються окремо. Знак результату визначається шляхом підсумовування по модулю 2 цифр, записаних в знакових розрядах. Остача нерухома, дільник зсувається праворуч. Як і при множенні з нерухомою сумою часткових добутків можна водночас виконувати підсумування і віднімання, зсув в регістрах Y,Z. Тобто 1 цикл може складатися з 1 такту, це дає прискорення відносно 1-го способу. Операційна схема
Р и сунок 2.6.1-Операційна схема Змістовний мікроалгоритм
Р и сунок 2.6.2-Змістовний мікроалгоритм Таблиця станів регістрів Таблиця 2.6.1- Таблиця станів регістрів
Закодований мікроалгоритм Таблиця 2.6.2- Таблиця кодування мікрооперацій
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 202; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.201.92 (0.015 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

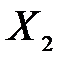 і
і  в прямому коді записати у формі з плаваючою комою (з порядком і мантисою, а також з характеристикою та мантисою), як вони зберігаються у пам’яті. На порядок відвести 8 розрядів, на мантису 16 розрядів (з урахуванням знакових розрядів).
в прямому коді записати у формі з плаваючою комою (з порядком і мантисою, а також з характеристикою та мантисою), як вони зберігаються у пам’яті. На порядок відвести 8 розрядів, на мантису 16 розрядів (з урахуванням знакових розрядів).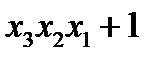 побудувати управляючий автомат Мура на тригерах (тип вибрати самостійно) і елементах булевого базису.
побудувати управляючий автомат Мура на тригерах (тип вибрати самостійно) і елементах булевого базису.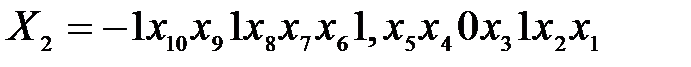 і
і  ,
, - двійкові цифри номера залікової книжки у двійковій системі числення (
- двійкові цифри номера залікової книжки у двійковій системі числення ( - молодший розряд).
- молодший розряд).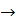 1101011000112
1101011000112
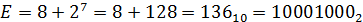
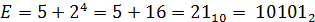
 + Y
+ Y 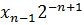 …+ Y
…+ Y 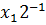 =
= )
)  + Y
+ Y 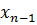 )
)  )
) 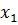 )
) 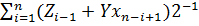 ;
;
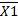
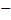
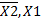
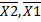

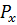 =8;
=8; 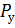 =5;
=5; 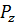 =1310=11012
=1310=11012 0 = 1.
0 = 1.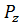 =12;
=12;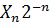 + Y
+ Y 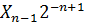 …+ Y
…+ Y 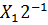 ;
; ;
;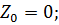


 +2(Y
+2(Y 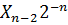 …+2Y
…+2Y 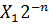 ));
)); ;
;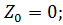
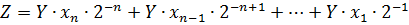 .
.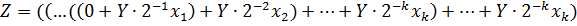 .
.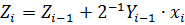 з початковими значеннями i=1, Y0=2-1Y, Z0=0.
з початковими значеннями i=1, Y0=2-1Y, Z0=0.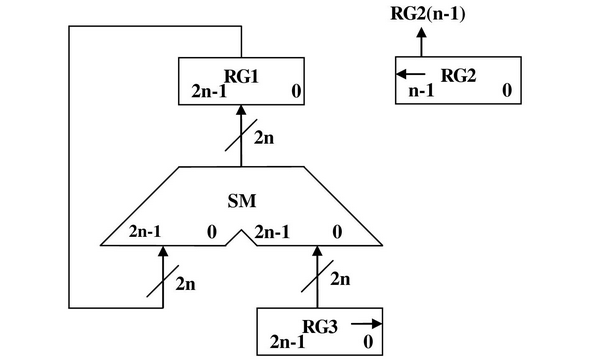
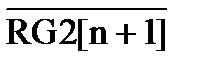 RG2:=l(RG2).0
RG2:=l(RG2).0
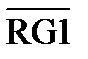 +1
+1
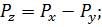
 +1
+1



