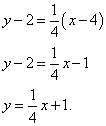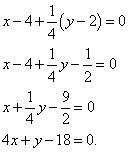Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Конспект занятия решения ключевых задач по теме «Уравнение касательной к графику функции»
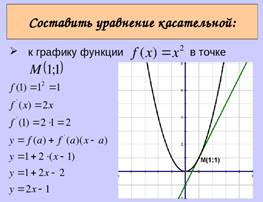
Теоретический материал для самостоятельного изучения Ход занятия: I. Мотивационно-ориентировочная часть 1. Актуализация опорных знаний. - Как вы понимаете термин «касательная»? - Что такое угловой коэффициент касательной? - Как влияет угловой коэффициент прямых на взаимное расположение прямых? - Расставьте этапы алгоритма составления уравнения касательной в правильном порядке. 2. Постановка цели занятия. Повторение. Геометрический смысл производной Производная функции в конкретной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или угловому коэффициенту этой касательной: f′(x0)= tgφ=k Уравнение касательной к графику функции f(x) в точке x0: y=f′(x0)⋅(x−x0)+f(x0). Уравнение касательной выводится из уравнения прямой. Выведем уравнение касательной, а затем - уравнение нормали к графику функции. Вспомним уравнение прямой с угловым коэффициентом: y = kx + b. В нём k - угловой коэффициент. Отсюда получаем следующую запись: y - y 0 = k ( x - x 0). Значение производной f '( x 0) функции y = f ( x ) в точке x 0 равно угловому коэффициенту k = tg φ касательной к графику функции, проведённой через точку M 0 ( x 0, y 0), где y 0 = f ( x 0). В этом состоит геометрический смысл производной. Таким образом, можем заменить k на f '( x 0) и получить следующее уравнение касательной к графику функции: y - y 0 = f '( x 0)( x - x 0). Алгоритм действий для нахождения уравнения касательной
Переходим к примерам. Для решений потребуется таблица производных. Решаем задачи вместе Пример 1. Составить уравнение касательной и уравнение нормали к графику функции Решение. Найдём ординату точки касания:
Найдём производную функции:
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
Теперь у нас есть всё, что требуется подставить в приведённую в теоретической справке запись, чтобы получить уравнение касательной. Получаем
В этом примере нам повезло: угловой коэффициент оказался равным нулю, поэтому отдельно приводить уравнение к общему виду не понадобилось. Теперь можем составить и уравнение нормали:
На рисунке ниже: график функции бордового цвета, касательная зелёного цвета, нормаль оранжевого цвета.
Следующий пример - тоже не сложный: функция, как и в предыдущем, также представляет собой многочлен, но угловой коэффициен не будет равен нулю, поэтому добавится ещё один шаг - приведение уравнения к общему виду. Пример 2. Составить уравнение касательной и уравнение нормали к графику функции Решение. Найдём ординату точки касания:
Найдём производную функции:
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
Подставляем все полученные данные в "формулу-болванку" и получаем уравнение касательной:
Приводим уравнение к общему виду (все буквы и числа, отличные от нуля, собираем в левой части, а в правой оставляем ноль):
Составляем уравнение нормали:
Пример 3. Составить уравнение касательной и уравнение нормали к графику функции Решение. Найдём ординату точки касания:
Найдём производную функции:
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
Находим уравнение касательной:
Перед тем, как привести уравнение к общему виду, нужно его немного "причесать": умножить почленно на 4. Делаем это и приводим уравнение к общему виду:
Составляем уравнение нормали:
Домашнее задание: повторить теоретический материал §48, стр.253 (учебник: Алгебра. 10-11 класс. Ш.А. Алимов) рассмотреть решение задач №1,2,3, составить краткий конспект занятия.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 237; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.157.45 (0.007 с.) |
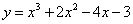 , если абсцисса точки касания
, если абсцисса точки касания 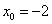 .
.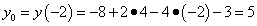 .
.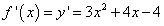 .
.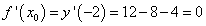 .
.


 , если абсцисса точки касания
, если абсцисса точки касания 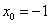 .
.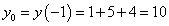 .
.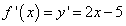 .
.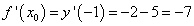 .
.
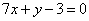

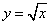 , если абсцисса точки касания
, если абсцисса точки касания 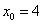 .
. .
.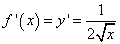 .
. .
.