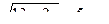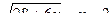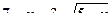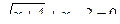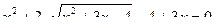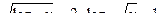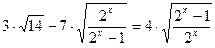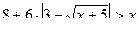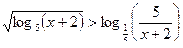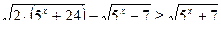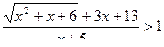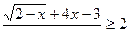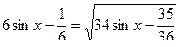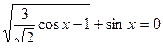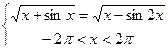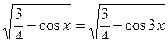Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Использование монотонности функций ⇐ ПредыдущаяСтр 7 из 7
при решении неравенств. В §5 части I мы описываем один из «нестандартных» приёмов, позволяющих в ряде задач получить ответ без большой технической работы в том случае, когда уравнение приводилось к эквивалентному виду f(x)=0, где f(x)-строго возрастающая или строго убывающая на рассматриваемом множестве функция. При решении неравенств в ряде случаев можно воспользоваться тем же приёмом.
Утверждение 6. Пусть f(x) возрастает на своей области определения
Если же f(x) убывает на
(неравенства противоположного знака разбираются аналогично).
Пример 12. Решить неравенство: Решение:
Левая часть возрастает на множестве Ответ:
Пример 13. Решить неравенство: Решение: Поскольку левая часть возрастает на области определения ( Ответ: (Сравните это решение с «честным»!).
Пример 14. Решить неравенство: Решение: Левая часть является убывающей функцией как разность убывающей и возрастающей. Нетрудно заметить, что при
Ответ:
§ 6. Задачи для самостоятельного решения.
Решите неравенства: 1.
2. 3.
4.
5.
6. . 7.
8.
9.
10.
11.
12.
§ 7. Контрольные задания
1. 2.
3.
4. 5. 6. 7. 8. Ответ: 9.
Часть III. Задачи, предлагавшиеся на экзаменах в МГУ. СПИСОК СОКРАЩЁННЫХ НАЗВАНИЙ ФАКУЛЬТЕТОВ. ММ - механико-математический, ВМК - вычислительной математики и кибернетики, Ф - физический, X - химический, Б - биологический, ПЧ - почвоведения, ГГ - географический, ГЛ - геологический, Э - экономический, ПС - психологический, ИСАА - институт стран Азии и Африки, СОЦ – социологический.
Решите уравнение (или неравенство): 1. (ГГ-93) 2. (ГГ-82) 3. (ГГ-96) 4. (Х-98) 5. (СОЦ-99) 7. (ПЧ-77) 8. (ПЧ-97) 9. (ГЛ-95) 10. (ГЛ-96) 11. (ПС-86) 12. (ПС-96) 13. (ГГ-99) 14. (ГГ-95) 15. (Э-83) 16. (ВМК-89) 17. (ВМК-91) 18. (Ф-88) 19. (Э-90) 20. (ГЛ-83) 21. (ГЛ-94) 22. (ПС-97) 23. (ГГ-99) 24. (Ф-80) 25. (Ф-85) 26. (Ф-93) 27. (Х-79) 28. (Х-96) 29. (Ф-79) 30. (Б-80) 31. (ПЧ-81) 32. (ПЧ-87) 33. (ГЛ-84) 34. (Э-95) 35. (ПС-88) 36. (ПС-89) 37. (ГЛ-01) 38. (Э-99) 39. (ВМК-94) 40. (ГГ-01) 41. (Б–83) 42. (ПЧ-98) 43. (ПС-01) 44. (ИСАА-91) 45. (ПС-93) 46. (ММ-98) 47. (Ф-97) 48. (Х-78) 49. (ГЛ-94) 50. (Э-88) 51. (ВМК-82) 52. (ММ-90) 53. (ПС-98) 54. (ВМК-84) 55. (ММ-88) 56. (ММ-82) 57. (ММ-85) 58. (ММ–91) 59. (ВМК-87) 60. (ВМК-92) 61. (Х-88) 62. (Х-94) 63. (ПЧ-82) 64. (ПЧ-96) 65. (ПС-87) 66. (ПС-95) 67. (СОЦ-00) 68. (ВМК-99) 69. (Х-92) 70. (ВМК-00)
Открытый урок по алгебре в 11 классе, тема: Иррациональные уравнения Ход урока Учитель: (на экране Слай д 1.) Альберт Эйнштейн сказал замечательные слова, вслушайтесь в них: “Ощущение тайны – наиболее прекрасное из доступных нам переживаний. Именно это чувство стоит у колыбели истинного искусства и настоящей науки”.
Вот и мы сегодня с вами в очередной раз попытаемся приоткрыть одну из тайн, которую дарит нам наука. Тема нашего сегодняшнего урока: учитель зачитывает тему и цель урока. Цель: (на экране Слайд 2.) 1. Познакомиться с понятием иррациональные уравнения и некоторыми методами их решения. 2. Развивать умение выделять главное в изучаемом материале, обобщать факты и понятия. Учитель: – Чтобы лучше усвоить новую тему, вспомним пройденный материал. I. Устная работа. Учитель дает задание: Разложить на множители: ( Cлайд 3).
Затем даются ответы на экране. Учитель озвучивает следующее задание: Найти область определения. (Слайд 4).
После ответов учащихся высвечиваются ответы на слайде. Учитель: В школьном курсе алгебры рассматриваются различные виды уравнений: Слайд 5.
Каждая из групп выбирает нужное уравнение. После ответов высвечиваются уравнения. Доп. Вопрос: Является ли число 3 решением вашего уравнения? Учитель: Является ли число Хо – корнем вашего уравнения? Слайд 6.
Учитель: А сейчас небольшая историческая справка, (выходит учащийся и рассказывает наизусть): История иррациональных чисел восходит к удивительному открытию Пифагорийцев ещё в VI веке до н.э. А началось все с простого, казалось бы вопроса – каким числом выражается длина диагонали квадрата со стороной 1? Пифагорийцы доказали, что √2 – нельзя выразить отношением некоторых целых чисел m и n. √2 – по их мнению вообще не было числом. Открыв новый математический объект они пришли в полное замешательство. В основе всеобщей гармонии мира, считали они, должны лежать целые числа и их отношения. Никаких других чисел они не знали. И вдруг эта гармония рушится – существуют величины, которые отношением целых чисел, в принципе – не являются. В переводе с латыни “irrationalis” – “неразумный”. Любопытно, что в средневековой Европе наряду с “irrationalis” в ходу был еще и другой термин “surdus” – “глухой” или “немой”. Судя по такому названию, математикам средневековья иррациональные числа представлялись чем-то настолько “неразумным”, что “ни высказать, ни выслушать”. Удивление и досада, с которыми древние математики в начале восприняли иррациональные числа, впоследствии, сменились интересом и пристальным вниманием к новым математическим объектам. “История иррациональных чисел”. (Слайд 7).
В переводе с латыни “irrationalis” – “неразумный”. Учитель: Вот и мы сейчас с таким же интересом и вниманием обратимся не к иррациональным числам, но к иррациональным уравнениям. Открываем тетради, записываем тему урока: “Иррациональные уравнения”.
Слайд 8. Высвечивается определение: Уравнения, в которых переменная содержится под знаком корня называются иррациональными.
Записать в тетрадь последнее уравнение: √х = х – 2 Учитель: Методы решения иррациональных уравнений, как правило, основаны на возможности перехода от иррационального к рациональному уравнению. Рассмотрим один из методов: возведение в степень обеих частей уравнения. Ребята, т.к. мы с вами выпускной класс и впереди предстоит сдача ЕГЭ, наша задача подготовиться к нему. Поэтому те уравнения, которые мы будем разбирать на уроке, взяты из разных сборников для подготовки к ЕГЭ. II. Работа в тетрадях.
а) Решить уравнение: Вопросы к учащемуся, который решает это уравнение:
х1 = 1, х2 = 4 Оба корня проверяем, подставляя в исходное уравнение. Видим, что х1 = 1 – не является корнем исходного уравнения, закрываем его магнитом на доске [посторонний корень]. Ответ: 4
Возведя обе части уравнения в нечетную степень, перешли к равносильному уравнению. Слайд 9. При возведении обеих частей уравнения: · в четную степень (показатель корня – четное число), возможно появление постороннего корня (проверка необходима); · в нечетную степень (показатель корня – нечетное число), получается уравнение, равносильное исходящему, (проверка не нужна). Учитель: Иногда удобнее решать иррациональные уравнения, используя равносильные преобразования, определить ОД3. (В этом случае проверку делать не надо). На доске: Вопрос к учащемуся у доски: г)
X2 = 0 посторонний корень. Ответ: 3
Ответ: Решений нет. Слайд 10. Решая иррациональные уравнения, используя равносильные преобразования – проверка не нужна. е) Уравнение, предлагаемое к самостоятельному решению.
Проверка: Подходят оба. Ответ: ±1 Один ученик вызывается к доске для проверки, рассказывает ход решения. III. Самостоятельная работа. Слайд 11.
После решения и сдачи самостоятельных работ на слайде появляются ответы. Слайд 12. Итог урока: – Иррациональные уравнения? При возведении обеих частей уравнения: · в четную степень (показатель корня – четное число), возможно появление постороннего корня (проверка необходима);
· в нечетную степень (показатель корня – нечетное число), получается уравнение, равносильное исходящему, (проверка не нужна). Учитель: Иногда удобнее решать иррациональные уравнения, используя равносильные преобразования, определить ОД3. (В этом случае проверку делать не надо). Решая иррациональные уравнения, используя равносильные преобразования – проверка не нужна. Учитель подводит итог урока глядя на слайд, опрашивая учащихся, благодарит за урок и говорит о том, что на следующем уроке познакомит ребят с другими методами решения замены переменной. Домашнее задание на доске.
|
||||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 89; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.144.217 (0.094 с.) |
 , тогда имеют место эквивалентности:
, тогда имеют место эквивалентности: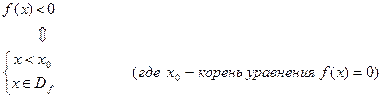



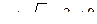
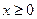 и при
и при  равна нулю, значит,
равна нулю, значит,  .
. ; 1).
; 1).
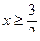 ), и
), и 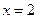 - корень соответствующего уравнения, то
- корень соответствующего уравнения, то  .
. .
.
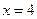 левая и правая части равны. Значит, решением неравенства будет пересечение множеств
левая и правая части равны. Значит, решением неравенства будет пересечение множеств 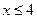 и
и 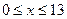 .
.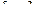 .
. Ответ:
Ответ: 
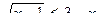 Ответ:
Ответ: 
 Ответ:
Ответ: 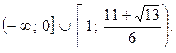
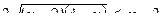 Ответ:
Ответ: 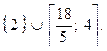
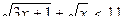 Ответ:
Ответ: 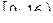
 Ответ:
Ответ: 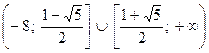
 Ответ:
Ответ: 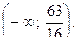
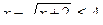 Ответ:
Ответ: 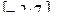
 Ответ:
Ответ: 
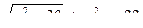 Ответ:
Ответ: 
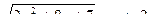 Ответ:
Ответ:  .
.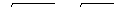 Ответ:
Ответ: 
 Ответ:
Ответ:  .
. Ответ:
Ответ: 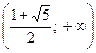 .
.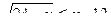 Ответ:
Ответ:  .
.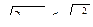 Ответ:
Ответ: 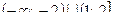 .
.  Ответ:
Ответ: 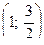 .
. Ответ:
Ответ:  .
. Ответ:
Ответ:  .
.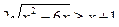
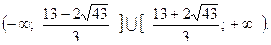
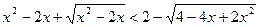 Ответ:
Ответ:  .
.