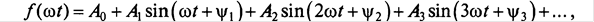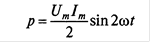Электрические цепи с несинусоидальными

ПЕРИОДИЧЕСКИМ НАПРЯЖЕНИЯМИ И ТОКАМИ

Основные понятия. Теорема Фурье

До сих пор рассматривались цепи с синусоидальными ЭДС, напряжениями и токами. В настоящей главе будут представлены электрические цепи, в которых эти величины изменяются с течением времени по периодическим законам, отличным от синусоидального. Причиной появления несинусоидальных ЭДС, напряжений и токов и могут быть как генераторы, так и потребители электрической энергии. ЭДС, индуктируемые в обмотках генератора, отличаются от синусоиды по нескольким причинам:

1) распределение магнитной индукции в воздушном зазоре генератора отличается от синусоиды (несимметричное положение ротора относительно статора, воздушные включения в магнитной цепи генератора, несимметрия обмотки ротора);

2) наличие пазов и зубцов в сердечниках ротора и статора;

3) в нагруженной электрической машине добавляется реакция якоря.

Несинусоидальные токи и напряжения возникают, если в цепи имеются потребители энергии с нелинейной ВАХ:

1) нелинейные активные сопротивления (полупроводниковые выпрямители, лампы накаливания, магнитные усилители и др.);

2) реактивные индуктивные сопротивления (катушки с ферромагнитным сердечником — дроссели);

3) реактивные емкостные сопротивления (нелинейные конденсаторы — варикапы).

Расчет линейных электрических цепей при наличии источника энергии, вырабатывающего несинусоидальную ЭДС. Режим работы такой электрической цепи рассматривают как совокупность налагающихся друг на друга синусоидальных режимов кратных частот. Для этого кривые несинусоидальных ЭДС напряжений и токов расскладывают в тригонометрический ряд, используя теорему Фурье:

всякая периодически изменяющаяся величина может быть представлена как сумма постоянной составляющей {независимой от времени) и ряда синусоидальных {гармонических) составляющих с кратными частотами

Синусоидальные составляющие несинусоидальных величин называются гармониками. Синусоидальная составляющая, частота которой равна частоте несинусоидальной величины, называется основной гармоникой, или первой гармоникой. Остальные гармоники, частота которых в два, в три и т.д. раза больше частоты несинусоидальной величины, называются гармониками высшего порядка (второй гармоникой, третьей гармоникой и т.д.).

Итак, согласно теореме Фурье всякую периодически изменяющуюся величину можно записать как сумму постоянной составляющей A0 и ряда синусоидальных составляющих:

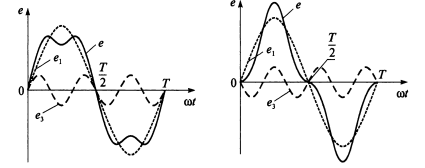
где А1 и А2 А3,... — амплитуды соответственно первой, второй, третьей и т.д. гармоник;

Ѱ1, Ѱ2, Ѱ3... — начальные фазы соответственно первой, второй, третьей и т.д. гармоник.

Графики, представленные на рис.А,Б подтверждают, что сложение синусоидальных величин с разными частотами и начальными фазами дает несинусоидальную кривую.

         

                              А)                      Б)

На рисунке А) показан график несинусоидальной ЭДС, содержащей две синусоидальные составляющие с одинаковыми нулевыми начальными фазами — основную (первую) е1 и имеющую ту же частоту, что и несинусоидальная кривая е2, и третью е3, имеющую тройную частоту

                 

На рисунке Б) показан график несинусоидальной ЭДС, содержащей две синусоидальные составляющие с различными начальными фазами — основную (первую) и третью

           

 Постоянная составляющая А0 является средним значением функции за период. Таким образом, если среднее значение функции за период равно нулю, то постоянная составляющая в ряде Фурье отсутствует. Так, в цепи переменного тока, например, с емкостью согласно выражению

                          

постоянная составляющая отсутствует и среднее значение мощности за период равно нулю Р = 0, А кривая мгновенной мощности р (см. рис.)

в цепи переменного тока с активным сопротивлением согласно выражению

                          

разложена на постоянную составляющую UI и переменную UI cos 2ωt

Среднее значение переменной составляющей за период равно нулю, как любой синусоидальной величины, поэтому среднее значение такой кривой за период равно постоянной составляющей, и активная мощность в цепи с активным сопротивлением определяется по известной формуле Р = UI.