Применение математических моделей

 

Для тех случаев, когда натурный эксперимент дорог или невозможен, широко применяется вычислительный или ими­тационный эксперимент, то есть проведение расчетов на математической модели. Алгоритмы и программы для проведения вычислительного экспери­мента являются обязательной и существенной частью систем автоматизированного проектирования (САПР).Для того, чтобы получить достоверные результаты при статистических испытаниях необходимо провести большое число экспериментов при случайном сочетании условий или факторов.

Простейшими планами эксперимента являются полные и дробные факторные планы. Полный факторный план для двух факторов x ₁ и x ₂ задается таблицей 1.

Таблица 1 - Полный факторный план для двух факторов

Номер испытания	Значения факторов
	x 1	x 2
1	+	-
2	+	+
3	-	+
4	-	-

 В таблице “+” обозначены максимальные значения фак­торов, “—” их минимальные значения. Как видно из таблицы 1, для того, чтобы исследовать вли­яние двух факторов на некоторую функцию цели достаточно провести четыре испытания при всех возможных сочетаниях факторов.

Обычно для контроля проводят еще испытания при сред­них значениях факторов. По полученным данным строят аппроксимирующий поли­ном и проверяют его адекватность по статистическим крите­риям. Полученный полином является математической моделью влияния рассматриваемых факторов на объект. Им можно воспользоваться для поиска наилучшего сочетания факторов.

Задача поиска наилучшего в некотором смысле сочетания факторов называется задачей оптимизации объекта.При этом условием или критерием оптимизации может быть мини­мум или максимум функции цели, например, минимум энер­гопотребления, минимум стоимости, максимум производи­тельности.В общем случае может быть несколько критериев, в том числе и противоречивых. Для поиска оптимума служат специальные численные методы, такие, как метод золотого сечения, метод градиент­ного спуска, метод симплексного планирования и ряд других.

Вопросы для самопроверки

1. Что называется имитационным экспериментом?

2. Что является предметом математической теории плани­рования эксперимента?

3. Что называется планом эксперимента?

4. Приведите примеры задачи оптимизации, укажите кри­терии оптимизации?

Раздел 4. ЗАДАНИЯ ДЛЯ КОНТРОЛЬНЫХ РАБОТ

И УКАЗАНИЯ ПО ИХ ВЫПОЛНЕНИЮ

 

К выполнению контрольной работы следует приступать после изучения теоретического материала по соответствую­щему разделу, рассмотрев и усвоив вопросы курса. Для этого необходимо проработать лекционный курс в системе дистанционного обучения Moodle, затем лабораторный курс, ответив на тестовые вопросы не менее, чем на 80%, что фиксируется системой. После этого появляется доступ к итоговому тестированию по дисциплине.

Решение задач контрольной работы должно сопровождаться краткими теоретическими пояснениями с приведением размерностей рассчитываемых величин.

 Блок-схемы алгоритмов должны вычерчи­ваться аккуратно с помощью чертежных принадлежностей.

Перед проработкой программы следует привести таблицу соответствия обозначений физических величин в модели, име­нам переменных в программе.

В конце работы следует расписаться, поставить дату, ука­зать использованную литературу и время (в часах), затра­ченное на выполнение работы.

Каждый студент получает индивидуальное задание, вари­ант задания выбирается по № зачетной книжки (студенческого билета). Пишется № студенческого билета, например

                                           16029

                                                 аб

под последними двумя цифрами записываются буквы- буквенные индексы параметров. По буквенным индексам в таблице выбираются исходные данные. Данные необходимо записать в работу в том порядке, в котором они изложены в таблице. Вычертить схему с указанием параметров, соответствующих шифру, по исходным данным произвести расчёт.

Первая задача выполняется по таблице 3,  вариант схемы выби­рается по таблице 2.

Вторая задача выполняется по таблице 4, при этом студент самостоятельно предлагает вариант рассматриваемого динамического процесса.

Третья задача выполняется в соответствии со специальностью студента, при этом вариант задачи также формируется студентом самостоятельно исходя из профессиональной деятельности, специальности и полученных знаний при изучении специальных дисциплин. Данные таблиц 5-8 могут носить лишь ориентировочный характер.

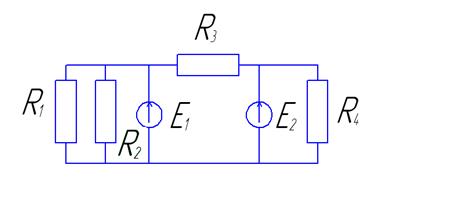
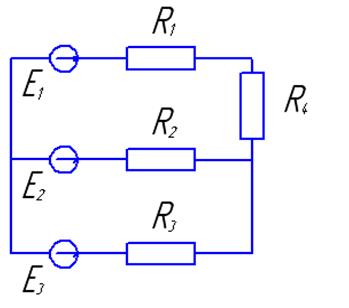
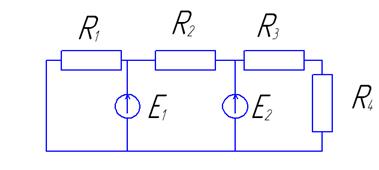
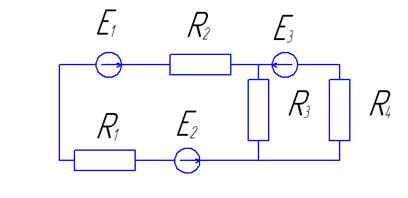
Стандартные подпрограммы численных методов могут быть взяты из рекомендованного списка источников литературы [2; 8; 9] или из приложения Б настоящих методических указаний.

Если работа не зачтена, то студент все исправления вы­полняет в конце той же тетради после подписи преподавателя, добавляя нужное количество листов. Какие-либо исправления в тексте, уже проверенном преподавателем, не допускаются.

Работы, выполненные с нарушением этих правил, не за­читываются, также как и работы, содержащие серьезные ошибки.

Задача 1.

Разработать математическую, графическую и численную модель, алгоритм для расчета электрической цепи постоянного тока по заданной схеме.

Методические рекомендации

Расчет электрической цепи постоянного тока состоит в определении неизвестных токов в ветвях.

 Решение может быть проведено одним из трех способов:

 1) по законам Кирх­гофа;

 2) методом контурных токов;

3) методом узловых по­тенциалов.

 

Таблица 2- Данные к задаче 1

Номер схемы	Схема к задаче 1
1
2
3
4

 

Таблица 3- Данные к задаче 1