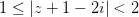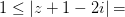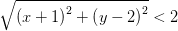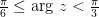Геометрическая интерпретация комплексных чисел.

Множество действительных чисел можно рассматривать как подмножество комплексных чисел, у которых $Im z= 0.$

Комплексное число z=x+iy изображают на координатной плоскости Oxy точкой с координатами (x;y). Эта плоскость называется комплексной плоскостью C (рисунок 1), ось Ox называется действительной осью, а ось Oy – мнимой осью. Таким образом, действительному числу z=x+0i=x отвечает точка на действительной оси, а мнимому числу z=0+iy=iy– точка на мнимой оси.

Можно также изображать комплексное число в виде радиус-вектора {x,y} и определять его, задавая его длину r и угол φмежду осью Ox и вектором.

Длина этого вектора называется модулем комплексного числа

|z|=r=x2+y2−−−−−−−√≥0,

а угол φ называется аргументом комплексного числа и обозначается Argz. Аргумент определяется с точностью до слагаемого 2πk(k=0,±1,±2,±3,...) и для положительных значений отсчитывается от оси Oxдо вектора против часовой стрелки, а для отрицательных значений – по часовой стрелке.

Значение аргумента, который принадлежит интервалу (−π,π], называется главным значением аргумента и определяется argz. Главное значение аргументу числа x+iy можно вычислять по формуле φ=argz=arctg(yx)+kπ, где k=0, если z находится в первой или четвертой четвертях, k=1, если z находится во второй четверти, k=−1, если z находится в третей четверти. Если x=Rez=0, то φ=π/2, когда y=Imz>0 и φ=−π/2, когда y=Imz<0. плоскость называется комплексной плоскостью C (рисунок 1), ось Ox называется действительной осью, а ось Oy – мнимой осью. Таким образом, действительному числу z=x+0i=x отвечает точка на действительной оси, а мнимому числу z=0+iy=y− точка на мнимой оси.

 

 

Решение квадратных уравнений с вещественными коэффициентами и комплексной переменной.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Решить квадратное уравнение.

1.508. z2+2z+5=0.

Решение.

D=22−4⋅1⋅5=4−20=−16

z1=−2+−16√2=−2+16√−1√2=−2+4i2=−1+2i;

z2=−2−−16√2=−2−16√−1√2=−2−4i2=−1−2i.

Ответ: z1=−1+2i; z2=−1−2i.

1.509. 4z2−2z+1=0.

Решение.

D=(−2)2−4⋅4⋅1=4−16=−12

z1=2+−12√8=2+12√−1√8=2+23√i8=14+3√4i;

z2=2−−12√8=2−12√−1√8=2−23√i8=14−3√4i.

Ответ: z1=14+3√4i; z2=14−3√4i.

Решить биквадратное уравнение

1.516. z4+18z2+81=0.

Решение.

Сделаем замену переменных:

t=z2.

Получаем квадратное уравнение:

t2+18t+81=0.

Решим его:

D=(18)2−4⋅1⋅81=324−324=0.

t1=−18+02=−9;

t2=−18−02=−9.

Далее сделаем обратную замену:

t1=t2=z21,2=z23,4⇒

⇒−9=z21,2⇒

⇒z1,2=±−9−−−√=±9√−1−−−√=±3i.

Ответ: z1,2=z3,4=±3i.

 

Домашнее задание

Решить биквадратное уравнение

1.517. z4+4z2+3=0.

Ответ: z1,2=±i z3,4=±3√i.

1.518. z4+9z2+20=0.

Ответ: z1,2=±2i z3,4=±5√i.

 

Геометрическая интерпретация комплексного числа

Добавить комментарий

Задана плоскость. Зададим на ней декартову систему координат.

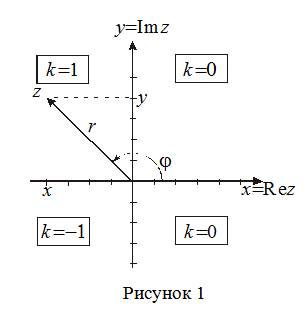
Данная плоскость называется комплексной. Ось называется вещественной, а ось 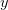— мнимой. На данном рисунке видно, что геометрически комплексное число представляет из себя вектор. Между алгебраической и геометрической интерпретациями комплексного числа существует биекция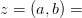

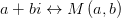
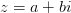Определение 1

Модулем комплексного числа называется корень разности квадратов его действительной и мнимой частей.
,

Определение 2

Расстояние между двумя векторами на комплексной плоскости вычисляется по формуле:

Определение 3

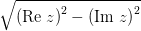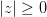
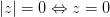
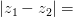
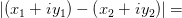
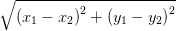
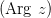Величина угла, который образует вектор, изображающий данное комплексное число на комплексной плоскости с вещественной осью называется аргументом этого комплексного числа . Угол, отсчитываемый от оси против часовой стрелки считается положительным, а по часовой — отрицательным.

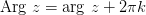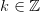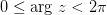, , , где 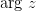- главное значение аргумента комплексного числа.

Пример 1

Задание:
Изобразите графически
Решение:

Ответ:

Пример 2

Задание:
Изобразите графически
Ответ:

Литература: