Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Еометрическая интерпретация комплексного числаСодержание книги
Поиск на нашем сайте
Еометрическая интерпретация комплексного числа Всякое комплексное число z = (x, y) можно изобразить как точку на плоскости с координатами x и y. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, при этом ось Ox называется действительной, а Oy - мнимой. Расстояние r точки z от нулевой точки, т. е. число
называется модулем комплексного числа z и обозначается символом | z |. Число
называем аргументом комплексного числа z и обозначаем символом θ = arg z. При заданном r углы, отличающиеся на Числа r и θ называют полярными координатами комплексного числа z. В этом случае z = (x, y) = (r cos θ, r sin θ) = r (cos θ + i sin θ) называется тригонометрической формой комплексного числа. Если z 1 = (r 1 cos θ 1, r 1 sin θ 1), z 2 = (r 2 cos θ 2, r 2 sin θ 2), то z 1 z 2 = (r 1 r 2 cos(θ 1 + θ 2), r 1 r 2 sin(θ 1 + θ 2)),
Для n -й степени числа z = (r cos θ, r sin θ) формула приобретает вид zn = (rn cos nθ, rn sin nθ). При r = 1 соотношение приобретает вид zn = (cos nθ, sin nθ) и называется формулой Муавра. Корень n -й степени из комплексного числа z имеет n различных значений, которые находятся по формуле
решения некоторых задач
Геометрическая интерпретация комплексного числа Комплексные числа изображаются на так называемой комплексной плоскости. Ось, соответствующая в прямоугольной декартовой системе координат оси абсцисс, называется действительной осью, а оси ординат - мнимой осью (рис. 1).
Комплексному числу
Например. На рисунке 3 на комплексной плоскости изображены числа
Модуль комплексного числа Комплексное число также можно изображать радиус-вектором Модуль любого ненулевого комплексного числа есть положительное число. Модули комплексно сопряженных чиселравны. Модуль произведения/частного двух комплексных чисел равен произведению/частному модулей каждого из чисел. Модуль вычисляется по формуле:
То есть модуль есть сумма квадратов действительной и мнимой частей заданного числа. Пример Задание. Найти модуль комплексного числа Решение. Так как
Ответ. Замечание Иногда еще модуль комплексного числа обозначается как Аргумент комплексного числа Угол Аргумент
На практике для вычисления аргумента комплексного числа обычно пользуются формулой:
Пример Задание. Найти аргумент комплексного числа Решение. Так как
Ответ. Аргумент действительного положительного числа равен У комплексно сопряженных чисел аргументы отличаются знаком (рис. 3).
Читать дальше: комплексно сопряженные числа.
Решение. D=22−4⋅1⋅5=4−20=−16 z1=−2+−16√2=−2+16√−1√2=−2+4i2=−1+2i; z2=−2−−16√2=−2−16√−1√2=−2−4i2=−1−2i. Ответ: z1=−1+2i; z2=−1−2i. 1.509. 4z2−2z+1=0. Решение. D=(−2)2−4⋅4⋅1=4−16=−12 z1=2+−12√8=2+12√−1√8=2+23√i8=14+3√4i; z2=2−−12√8=2−12√−1√8=2−23√i8=14−3√4i. Ответ: z1=14+3√4i; z2=14−3√4i. Решение. Сделаем замену переменных: t=z2. Получаем квадратное уравнение: t2+18t+81=0. Решим его: D=(18)2−4⋅1⋅81=324−324=0. t1=−18+02=−9; t2=−18−02=−9. Далее сделаем обратную замену: t1=t2=z21,2=z23,4⇒ ⇒−9=z21,2⇒ ⇒z1,2=±−9−−−√=±9√−1−−−√=±3i. Ответ: z1,2=z3,4=±3i.
Домашнее задание Решить биквадратное уравнение 1.517. z4+4z2+3=0. Ответ: z1,2=±i z3,4=±3√i. 1.518. z4+9z2+20=0. Ответ: z1,2=±2i z3,4=±5√i.
Определение 1 Модулем комплексного числа Определение 2 Расстояние между двумя векторами на комплексной плоскости вычисляется по формуле: Определение 3 Величина угла, который образует вектор, изображающий данное комплексное число на комплексной плоскости с вещественной осью называется аргументом этого комплексного числа
Пример 1 Задание: Пример 2 Задание: Литература:
Таблица лучших: Геометрическая интерпретация комплексных чисел (лекции)
Поделиться ссылкой:
Что такое "геометрическая интерпретация комплексного числа"? Ответ сокращённый и точный. Геометрическая интерпретация комплексных чисел состоит в том, что каждому комплексному числу z = x + yi ставится в соответствие точка (x, y) координатной плоскости таким образом, что действительная часть комплексного числа представляет собой абсциссу, а коэффициент при мнимой части – ординату точки.
Комплексные числа Комплексным числом называют выражение вида a + bi, где a и b - вещественные числа, а i - символ, удовлетворяющий соотношению i 2 = – 1. Если z = a + bi, то числа a и b называют соответственно вещественной и мнимою частью числа z (обозначение:
Каждое вещественное число a можно рассматривать как комплексное число a + 0 i. Если на плоскости выбрать систему координат, то можно установить взаимно однозначное соответствие между комплексными числами и точками плоскости, при котором числу a + bi соответствует точка с координатами (a, b). При этом умножение на комплексное число z приобретает следующую геометрическую интерпретацию. Пусть r - расстояние от нуля до z, j - угол, на который нужно повернуть вокруг нуля луч, содержащий положительные вещественные числа, чтобы получить луч Oz. Тогда умножение на число z - это композиция гомотетии с коэффициентом r (с центром в нуле) и поворота на угол j. Числа r и j называют соответственно модулем и аргументом числа z (обозначение: r = | z |, j = arg z). По-другому геометрическую интерпретацию произведения комплексных чисел можно сформулировать так: при умножении комплексных чисел их модули перемножаются, а аргументы складываются. Зная геометрическую интерпретацию комплексных чисел, легко научиться их делить: для этого нужно делить модули и вычитать аргументы. Деление можно ввести также и чисто алгебраически. Для каждого комплексного числа z = a + bi имеет место очевидное равенство
Поэтому
Тот факт, что произведение комплексных чисел, с одной стороны, вычисляется чисто алгебраически, а с другой стороны, имеет геометрическую интерпретацию, иногда бывает полезным при решении задач планиметрии. Как правило, решение, использующее комплексные числа, в действительности использует только векторы и поворот. Но иногда комплексные числа позволяют взглянуть на теоремы планиметрии с новой точки зрения и, что гораздо важнее, глубже понять их природу. Очень простую интерпретацию на языке комплексных чисел имеет инверсия с центром в нуле: она отображает число z в число
29.20. Пусть a, b, c, d - комплексные числа, причем углы a 0 b и c 0 d равны и противоположно ориентированы. Докажите, что тогда
Будем говорить, что треугольники ABC и A ¢ B ¢ C ¢ собственно подобны, если существует поворотная гомотетия, которая переводит A в A ¢, B в B ¢, C в C ¢. 29.21. Докажите, что если треугольники abc и a ¢ b ¢ c ¢ на комплексной плоскости собственно подобны, то
29.22. Докажите, что треугольники abc и a ¢ b ¢ c ¢ собственно подобны, тогда и только тогда, когда
29.23. Пусть a и b - комплексные числа, лежащие на окружности с центром в нуле, u - точка пересечения касательных к этой окружности в точках a и b. Докажите, что u = 2 ab /(a + b). 29.24. Пусть a - комплексное число, лежащее на единичной окружности S с центром в нуле, t - вещественное число (точка, лежащая на вещественной оси). Пусть, далее, b - отличная от a точка пересечения прямой at с окружностью S. Докажите, что
29.25. Даны треугольник ABC и прямая l, проходящая через центр O вписанной окружности. Обозначим через A 1 (соответственно B 1, C 1) основание перпендикуляра, опущенного на прямую l из точки A (соответственно B, C), а через A 2 (соответственно B 2, C 2) обозначим точку вписанной окружности, диаметрально противоположную точке касания со стороной BC (соответственно CA, AB). Докажите, что прямые A 1 A 2, B 1 B 2, C 1 C 2, пересекаются в одной точке, и эта точка лежит на вписанной окружности. 29.26. а) Докажите, что все окружности и прямые задаются уравнениями вида
где A и D - вещественные числа, а c - комплексное число. Наоборот, докажите, что любое уравнение такого вида задает либо окружность, либо прямую, либо точку, либо пустое множество. б) Докажите, что при инверсии окружности и прямые переходят в окружности и прямые. 29.27. Пусть точки A *, B *, C *, D * являются образами точек A, B, C, D при инверсии. Докажите, что: а)
б) Ð(DA, AC) – Ð(DB, BC) = Ð(D * B *, B * C *) – Ð(D * A *, A * C *). 29.28. Докажите, что точки, соответствующие комплексным числам a, b, c, лежат на одной прямой тогда и только тогда, когда число
б) Докажите, что точки, соответствующие комплексным числам a, b, c, d, лежат на одной окружности (или на одной прямой) тогда и только тогда, когда число
29.29 *. а) Докажите, что если A, B, C и D - произвольные точки плоскости, то AB · CD + BC · AD ³ AC · BD (неравенство Птолемея). б) Докажите, что если A 1, A 2, … A 6 - произвольные точки плоскости, то
в) Докажите, что (нестрогое) неравенство Птолемея обращается в равенство тогда и только тогда, когда ABCD - (выпуклый) вписанный четырехугольник. г) Докажите, что неравенство из задачи б) обращается в равенство тогда и только тогда, когда A 1… A 6 - вписанный шестиугольник. 29.30 *. Докажите, что если a, b, c и d - длины последовательных сторон выпуклого четырехугольника ABCD, а m и n - длины его диагоналей, то m 2 n 2 = a 2 c 2 + b 2 d 2 – 2 abcd cos (A + C) (Бретшнейдер). 29.31 *. а) Даны точка X и треугольник ABC. Докажите, что
где a, b, c - длины сторон треугольника. б) На сторонах BC, CA, AB взяты точки A 1, B 1, C 1. Пусть a, b, c - длины сторон треугольника ABC, a 1, b 1, c 1 - длины сторон треугольника A 1 B 1 C 1, S - площадь треугольника ABC. Докажите, что
29.32 *. На сторонах аффинно правильного многоугольника A 1 A 2… An с центром O внешним образом построены квадраты Aj + 1 AjBjCj + 1 (j = 1,…, n). Докажите, что отрезки BjCj и OAj перпендикулярны, а их отношение равно
29.33 *. На сторонах выпуклого n -угольника внешним образом построены правильные n -угольники. Докажите, что их центры образуют правильный n -угольник тогда и только тогда, когда исходный n -угольник аффинно правильный. 29.34 *. Вершины треугольника соответствуют комплексным числам a, b и c, лежащим на единичной окружности с центром в нуле. Докажите, что если точки z и w изогонально сопряжены, то
29.35 *. Точки Z и W изогонально сопряжены относительно правильного треугольника. При инверсии относительно описанной окружности точки Z и W переходят в Z * и W *. Докажите, что середина отрезка Z * W * лежит на вписанной окружности. 29.36 *. Точки Z и W изогонально сопряжены относительно правильного треугольника ABC с центром O; M - середина отрезка ZW. Докажите, что Ð AOZ + Ð AOW + Ð AOM = n p (углы ориентированы).
еометрическая интерпретация комплексного числа Всякое комплексное число z = (x, y) можно изобразить как точку на плоскости с координатами x и y. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, при этом ось Ox называется действительной, а Oy - мнимой. Расстояние r точки z от нулевой точки, т. е. число
называется модулем комплексного числа z и обозначается символом | z |. Число
называем аргументом комплексного числа z и обозначаем символом θ = arg z. При заданном r углы, отличающиеся на Числа r и θ называют полярными координатами комплексного числа z. В этом случае z = (x, y) = (r cos θ, r sin θ) = r (cos θ + i sin θ) называется тригонометрической формой комплексного числа. Если z 1 = (r 1 cos θ 1, r 1 sin θ 1), z 2 = (r 2 cos θ 2, r 2 sin θ 2), то z 1 z 2 = (r 1 r 2 cos(θ 1 + θ 2), r 1 r 2 sin(θ 1 + θ 2)),
Для n -й степени числа z = (r cos θ, r sin θ) формула приобретает вид zn = (rn cos nθ, rn sin nθ). При r = 1 соотношение приобретает вид zn = (cos nθ, sin nθ) и называется формулой Муавра. Корень n -й степени из комплексного числа z имеет n различных значений, которые находятся по формуле
решения некоторых задач
Геометрическая интерпретация комплексного числа Комплексные числа изображаются на так называемой комплексной плоскости. Ось, соответствующая в прямоугольной декартовой системе координат оси абсцисс, называется действительной осью, а оси ординат - мнимой осью (рис. 1).
Комплексному числу
Например. На рисунке 3 на комплексной плоскости изображены числа
Модуль комплексного числа Комплексное число также можно изображать радиус-вектором Модуль любого ненулевого комплексного числа есть положительное число. Модули комплексно сопряженных чиселравны. Модуль произведения/частного двух комплексных чисел равен произведению/частному модулей каждого из чисел. Модуль вычисляется по формуле:
То есть модуль есть сумма квадратов действительной и мнимой частей заданного числа. Пример Задание. Найти модуль комплексного числа Решение. Так как
Ответ. Замечание Иногда еще модуль комплексного числа обозначается как Аргумент комплексного числа Угол Аргумент
На практике для вычисления аргумента комплексного числа обычно пользуются формулой:
Пример Задание. Найти аргумент комплексного числа Решение. Так как
Ответ. Аргумент действительного положительного числа равен У комплексно сопряженных чисел аргументы отличаются знаком (рис. 3).
Читать дальше: комплексно сопряженные числа.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 297; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.011 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

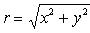
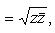
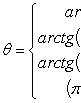
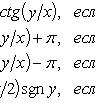
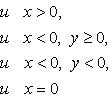

 , соответствуют одному и тому же числу. В этом случае записываем
, соответствуют одному и тому же числу. В этом случае записываем 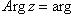

 называем главным значением аргумента.
называем главным значением аргумента.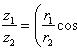
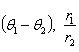

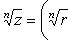
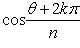
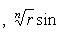

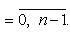 (1)
(1)
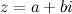 будет однозначно соответствовать на комплексной плоскости точка
будет однозначно соответствовать на комплексной плоскости точка 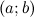 :
: 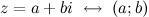 (рис. 2). То есть на действительной оси откладывается действительная часть комплексного числа, а на мнимой - мнимая.
(рис. 2). То есть на действительной оси откладывается действительная часть комплексного числа, а на мнимой - мнимая.
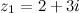 ,
, 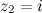 и
и 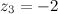 .
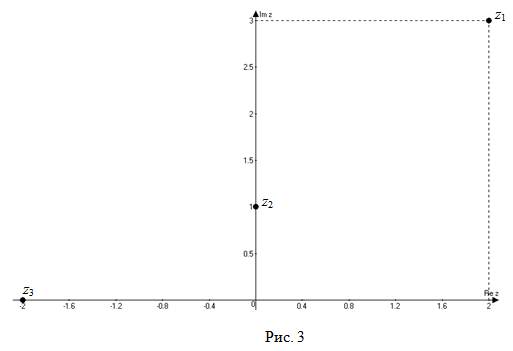
.
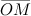 (рис. 2). Длина радиус-вектора, изображающего комплексное число
(рис. 2). Длина радиус-вектора, изображающего комплексное число 
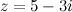
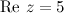 ,
, 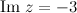 , то искомое значение
, то искомое значение
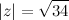
 или
или 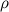 .
.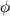 между положительным направлением действительной оси и радиус-вектора
между положительным направлением действительной оси и радиус-вектора 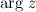 .
.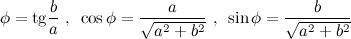
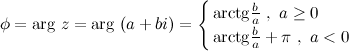
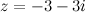
 , то в выше приведенной формуле будем рассматривать вторую строку, то есть
, то в выше приведенной формуле будем рассматривать вторую строку, то есть
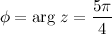
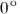 , действительного отрицательного -
, действительного отрицательного -  или
или  . Чисто мнимые числа с положительной мнимой частью имеют аргумент равный
. Чисто мнимые числа с положительной мнимой частью имеют аргумент равный 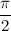 , с отрицательной мнимой частью -
, с отрицательной мнимой частью - 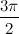 .
.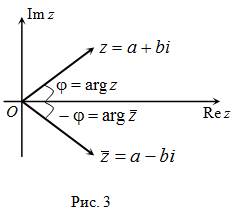
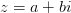 называется корень разности квадратов его действительной и мнимой частей.
называется корень разности квадратов его действительной и мнимой частей.

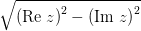 ,
, 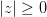
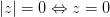
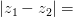
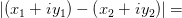
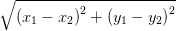
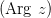 . Угол, отсчитываемый от оси против часовой стрелки считается положительным, а по часовой — отрицательным.
. Угол, отсчитываемый от оси против часовой стрелки считается положительным, а по часовой — отрицательным.
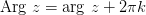 ,
, 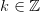 ,
, 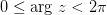 , где
, где 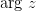 - главное значение аргумента комплексного числа.
- главное значение аргумента комплексного числа.