
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лучистый теплообмен в замкнутой системе телСодержание книги
Поиск на нашем сайте Под замкнутой системой понимается система тел, которая ограничивает пространство со всех сторон. В замкнутой системе, состоящей из двух серых тел произвольной формы результирующий тепловой поток на поверхность 2 находим из выражения
Разделив числитель и знаменатель в правой части этого выражения на коэффициент лучеиспускания абсолютно черного тела Со и принимая во внимание, что в соответствие со свойством взаимности средних угловых коэффициентов излучения
(150) Выражение (150) для результирующего теплового потока записывают обычно в виде
Отсюда легко получить более простые частные формулы, соответствующие отдельным конкретным случаям. Так для случая двух больших параллельных поверхностей, расположенных на близком расстоянии φ 12 = φ 21 = 1 значение С легко вычисляются по формуле
Для случая двух концентрических шаровых поверхностей или двух коаксиальных цилиндров (одно тело внутри другого) угловой коэффициент с внутреннего тела на внешнее φ 12 = 1, а с внешнего тела на внутреннее
3.6 теплообмен излучением при установке экранов В тех случаях, когда требуется уменьшить лучистый тепловой поток, на его пути могут быть установлены экраны, т.е. тонкие листы из непрозрачного материала, например металла. Предположим, что имеются две большие параллельные плоские поверхности 1 и 2, расположенные одна против другой так, что расстояние между ними мало по сравнению с их размерами. Пусть каждая из поверхностей F и их температуры соответственно равны Т 1 и Т 2, а коэффициенты излучения известны и одинаковы С 1 = С 2. Для такой пары поверхностей приведенный коэффициент излучения будет равен
Вставим в промежуток между этими поверхностями тонкий металлический экран, коэффициент излучения для обеих поверхностей пусть также будет С. Так как экран сделан из тонкого металлического листа, то обе его стороны будут иметь одинаковую температуру Т э, которая пока неизвестна. Найти ее можно, приравняв поток тепла, передаваемый с поверхности 1 к экрану, и поток тепла, передаваемый с экрана на поверхность 2:
Решив это уравнение, легко найти температуру экрана:
Обозначим тепловой поток, передаваемый с поверхности 1 на поверхность 2 при установке одного экрана, через Q 1. Эту величину определим, воспользовавшись найденными выше значениями Т э
Следовательно, при установке одного экрана лучистый тепловой поток уменьшится в два раза, если при этом приведенный коэффициент излучения остается без изменений. Если таких экранов установлено последовательно п штук, то можно показать, что лучистый тепловой поток, передаваемый при этом будет уменьшен в (п + 1) раз и составит:
Если установлен только один экран с С э, значительно меньше коэффициента излучения поверхностей, между которыми он установлен, то количество передаваемого тепла будет уменьшено не в два раза, а в значительно большей степени. Это обеспечивается резким снижением степени черноты экрана. В этом случае приведенный коэффициент излучения без экрана по-прежнему будет равен
а при установке экрана он уменьшается до величины Температура экрана в этом случае не изменяется, так как приведенный коэффициент излучения С ´ одинаков с обеих сторон экрана. Но количество передаваемого тепла уменьшится более чем в два раза. А именно: в
3.7 Излучение через отверстие в печных стенах В печах части приходится иметь дело с излучением через открытые рабочие окна, гляделки и другие отверстия, сделанные в сравнительно толстых печных стенах. Теоретически это можно представить следующим образом. Возьмем полый прямой круглый цилиндр (рис. 35). Пусть одно основание его F 1 нагрето до температуры Т 1 и излучает энергию по закону косинусов во всех направлениях внутрь полости. Пусть температура другого основания цилиндра F 2, воспринимающего тепло будет настолько ниже Т 2, что собственным его излучением можно пренебречь. Боковую поверхность цилиндра будем считать «идеальной обмуровкой», т.е. поверхностью совершенно не пропускающей тепло наружу. Полное количество тепла, передаваемое с одного основания цилиндра на другое, складывается из тепла, передаваемого прямым излучением с F 1 на F 2 и тепла, «отраженного» стенками идеальной обмуровки на поверхность F 2.
Решив эту задачу, была получена формула для определения общего количества лучистой энергии, передаваемой с одного основания цилиндра на другое. Передача энергии происходит прямым излучением, а также отражением и излучением от боковой поверхности цилиндра, являющейся идеальной обмуровкой (вывод формулы из-за большой громоздкости не приводится):
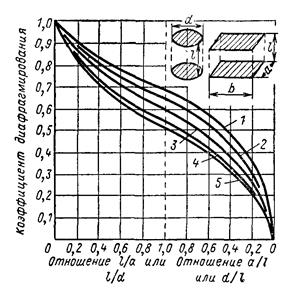
где С – приведенный коэффициент излучения, Вт/м2К4; ф – коэффициент диафрагмирования, который учитывает как прямое излучение с поверхности F 1 на поверхность F 2, так и косвенное излучение, передаваемое обмуровкой. Численные значения коэффициентов ф зависят только от соотношения между диаметром цилиндра и его длиной (эти зависимости приводятся на специальном графике). Пример Температура внутри печи t 1 = 1400 оС, температура цеха t 2 = 20 оС. В одной из стенок, толщина которой равна 250 мм, находится открытое окно 500×750 мм. Требуется определить тепловые потери излучением через это окно. Прежде всего определим соотношение размеров окна и толщины стенки:
Зная эти отношения, по рис. 36 находим коэффициент диафрагмирования ф, который равен 0, 728.
Затем по формуле (160) определяем искомые потери
где Т 1 – температура печи, К; Т 2 – температура цеха, К; Тм – температура дверцы, К; F – площадь отверстия, м2; См – коэффициент лучеиспускания металлической дверцы, который принимают равным 5,22 Вт/м2К4. Решив систему этих двух уравнений, было установлено, что тепловые потери излучением через окно, закрытое металлической дверцей, равны:
а температура самой дверцы Для уменьшения тепловых потерь и понижения температуры дверцы на ее внутренней стороне часто устанавливают металлический щиток, являющийся дополнительным экраном. При установке такого щитка тепловые потери снижаются примерно в 1,5 раза по сравнению с потерями через металлическую дверцу, не снабженную щитком.
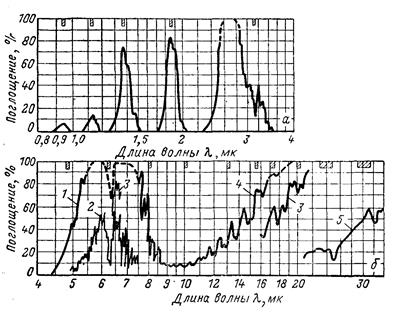
3. 8 Лучистый теплообмен в газовой среде Особенности излучения газов и паров Одно- и двухатомные газы (гелий, водород, кислород, азот и др.) практически являются прозрачными (диатермичными) для теплового излучения. Трехатомные и многоатомные газы обладают большой излучательной и поглощательной способностью (СО 2, Н 2 О, SО 2). В отличие от твердых и жидких тел излучение газов носит объемный характер, т.к. в нем участвуют все микрочастицы газа, заключенного в рассматриваемом объеме. Поэтому поглощательная способность газа изменяется в зависимости от плотности и толщины газового слоя. Излучение газов носит избирательный (селективный) характер. Они поглощают и излучают энергию только в определенных интервалах длин волн (рис. 29, 30).
Газы излучают и поглощают интервалах длин волн - полосах, расположенных в различных частях спектра. Энергию длин волн вне этих полос газы не поглощают и не излучают. Протяженность и место расположения на спектре полос излучения (поглощения) лучистой энергии различны для различных газов. Для двуокиси углерода и водяного пара наибольшее практическое значение имеют следующие основные полосы (в мк): - для СО 2
- для Н 2 О
Спектральные полосы поглощения СО 2 частично совпадают с полосами поглощения Н 2 О. Двуокись углерода обладает более узкими полосами поглощения чем водяной пар. Поэтому интенсивность излучения и степень черноты водяного пара больше, чем у двуокиси углерода. Излучательная способность для углекислого газа и водяного пара по опытным данным может быть представлена зависимостями:
Приведенные зависимости показывают, что излучение газов значительно отклоняется от закона четвертых степеней абсолютной температуры Стефана-Больцмана. Таким образом, излучательная и поглощательная способности газов являются функциями:
где р – парциальное давление, ат; ℓ – эффективная толщина слоя, м. В основу практических расчетов излучения газов положен закон Стефана-Больцмана. Однако, для удобства практических расчетов излучение газов связывают с излучением абсолютно черного тела, вводя понятие степени черноты газа:
где εг – степень черноты газа, qг – количество тепла, передаваемого излучением газа, Вт/м2. И тогда плотность излучения газа определяется по формуле:
Уравнение переноса лучистой энергии При прохождении тепловых лучей в поглощающей газовой среде поглощенная лучистая энергия переходит в теплоту и излучается этой средой. В результате процессов поглощения и переизлучения происходит перенос лучистой энергии и тепла в поглощающей среде. Пусть имеется слой газа, на который падает поток лучистой энергии, имеющий сплошной спектр. Некоторая часть лучей при этом пройдет через поглощающую среду без изменения интенсивности, и только лучи, имеющие определенную длину, будут поглощаться газом. Интенсивность потока лучистой энергии по мере прохождения через слой газа будет постепенно уменьшаться (рис. 31).
Приближенно принимается, что ослабление интенсивности излучения по отдельным длинам волн при прохождении через слой поглощающего газа толщиной dℓ уменьшается пропорционально этой интенсивности и бесконечно малому прохождению пути луча dℓ
Здесь kλ – коэффициент поглощения или правильнее коэффициент ослабления луча. Это выражение является основным законом переноса лучистой энергии в поглощающей среде – законом Бугера. Его можно представить в виде:
Полагая, что при ℓ = 0 il = ilо = 0, после интегрирования последнего уравнения получим:
откуда
Согласно закону Стефана-Больцмана излучательная способность для отдельных полос излучения среды представится зависимостью:
Интенсивность излучения ilо находится по закону Планка. Поглощательная способность определяется по отношению лучистой энергии, поглощенной средой в слое толщиной ℓ, к энергии излучения, падающей на этот слой il= 0
При прохождении теплового луча через слой из смеси газов, эффект поглощения будет тем больше, чем больше парциальное давление поглощающего газа. В соответствие с законом Бэра коэффициент ослабления равен:
где bλ – температурный коэффициент; Рi – парциальное давление газа. Таким образом, выражение для спектральной поглощательной способности плоского слоя газа, в соответствие с законами Бугера и Бэра принимает вид:
Если считать, что интегральная степень черноты газа εг определяется выражением
где Ег – собственное излучение газа, то формула для определения εг будет иметь вид
Интегральная поглощательная способность газа будет иметь вид
Несмотря на очевидное различие степени черноты газа и его поглощательной способности в инженерных расчетах обычно полагают эти величины одинаковыми. Таким образом, для определения поглощательной и излучательной энергии среды необходимо располагать данными по спектрам поглощения и излучения, а также по коэффициентам ослабления для всех полос спектра. Коэффициент ослабления луча в общем случае не является постоянной величиной. Он зависит от природы излучающей среды, длины волны и температуры. Вследствие этого коэффициенты оказываются весьма различными не только для отдельных полос спектра, но существенно изменяются в пределах одной и той же полосы. Приведенные уравнения лучистой энергии относятся к поглощательной среде, переизлучения которой незначительно, распределение температуры по объему газа является равномерным.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 426; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |

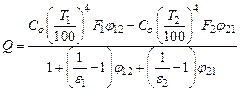 . (149)
. (149)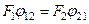 , получим окончательно
, получим окончательно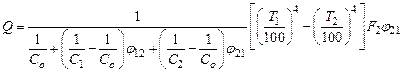 .
.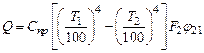 ,
,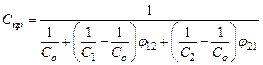
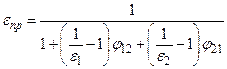 .
. 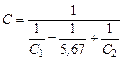 , Вт/м2К4. (151)
, Вт/м2К4. (151)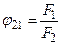 и при этом
и при этом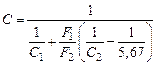 , Вт/м2К4. (152)
, Вт/м2К4. (152)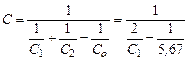 , Вт/м2К4. (153)
, Вт/м2К4. (153)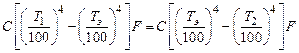 . (154)
. (154)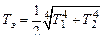 , К. (155)
, К. (155)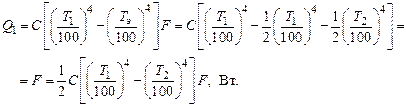 (156)
(156) 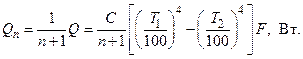 (157)
(157)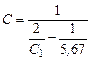 , Вт/м2К4,
, Вт/м2К4,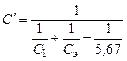 , Вт/м2К4. (158)
, Вт/м2К4. (158)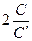 раза. Чем меньше С э, тем меньше С ´ и тем больше это отношение.
раза. Чем меньше С э, тем меньше С ´ и тем больше это отношение.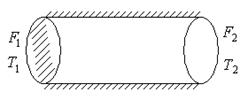
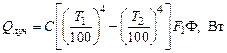 , (160)
, (160)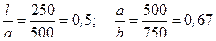 .
.
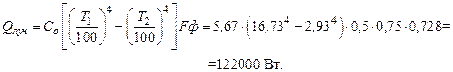 В печах нередко встречаются окна топок и различные смотровые отверстия, которые закрываются не заслонками, футерованными огнеупорным кирпичом, а простыми металлическими дверцами. При закрытой дверце через такие отверстия происходит потеря тепла по законам излучения, т.к. в этом случае металлическая дверца играет роль экрана. Условия лучистого теплообмена с различных сторон такого экрана несимметричны. Тепловые потери при закрытой дверце можно определить из системы двух уравнений. Эти потери должны быть равны лучистому тепловому потоку, поглощаемому внутренней поверхностью дверцы. Но они также равны свободному излучению с наружной поверхности дверцы в сторону цеха:
В печах нередко встречаются окна топок и различные смотровые отверстия, которые закрываются не заслонками, футерованными огнеупорным кирпичом, а простыми металлическими дверцами. При закрытой дверце через такие отверстия происходит потеря тепла по законам излучения, т.к. в этом случае металлическая дверца играет роль экрана. Условия лучистого теплообмена с различных сторон такого экрана несимметричны. Тепловые потери при закрытой дверце можно определить из системы двух уравнений. Эти потери должны быть равны лучистому тепловому потоку, поглощаемому внутренней поверхностью дверцы. Но они также равны свободному излучению с наружной поверхности дверцы в сторону цеха: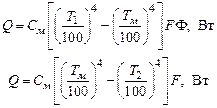 (161)
(161)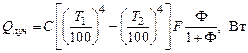 , (162)
, (162)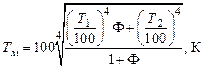 . (163)
. (163)
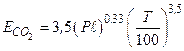 , (164)
, (164)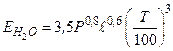 . (164а)
. (164а)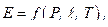 (165)
(165)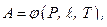 (166)
(166)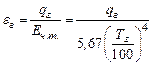 , (167)
, (167)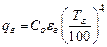 , Вт/м2. (168)
, Вт/м2. (168)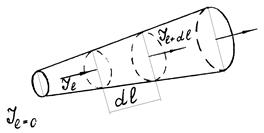
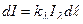 . (169)
. (169)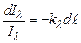 . (170)
. (170)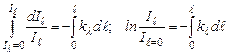 (171)
(171)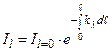 . (172)
. (172)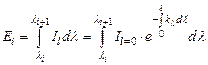 . (173)
. (173)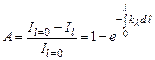 . (174)
. (174)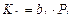 , (175)
, (175)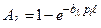 . (176)
. (176)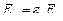 ,
, 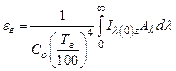 . (177)
. (177)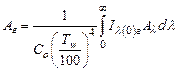 . (178)
. (178)


