
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приазовский государственный техническийСодержание книги
Поиск на нашем сайте
Маслов в.а. Теплотехника Для металлургов (часть II) Мариуполь 200 8
Министерство образования и науки Украины Приазовский государственный технический университет Маслов в.а. Теплотехника Для металлургов (часть II) Мариуполь 200 8
ББК 31,35 УДК 669.019.021/09.041
В.А Маслов Теплотехника, т 2. Мариуполь, ПГТУ, 2008г., с..
Во втором томе учебника рассмотрен комплекс вопросов теплообмена, механики жидкости и газа, приведены основные понятия, законы и их выводы, а также рассмотрены практические рекомендации их использования. В завершающей части на основе приведенной общей схемы печной установки рассмотрены вопросы теплотехнической характеристики печи, теплового баланса, использования огнеупоров, а также принципиальные вопросы утилизации тепла отходящих дымовых газов. Приведенные материалы соответствуют стандарту высшего образования Украины по направлению 0904 «Металлургия». Предложенный учебник рекомендован студентами направления «Металлургия». Иллюстраций, таблиц, библиографий.
Компьютерный набор, верстка Л.Н.Сапрыкина
ISBN 966 - 7559
© Маслов В.А., 2008
оглавление
ЧАСТЬ II РАЗДЕЛ 1. ТЕПЛОПРОВОДНОСТЬ ПЛОСКОЙ СТЕНКИ
Основываясь на законе Фурье, можно вывести расчетные формулы теплопроводности.
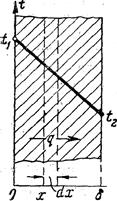
Однородная стенка. Рассмотрим однородную стенку толщиной δ (рис.6). Коэффициент теплопроводности материала постоянен и равен λ. На наружных поверхностях стенки поддерживаются постоянные температуры t1 и t2. Температура изменяется только в направлении оси х, перпендикулярной плоскости стенки. Следовательно, в этом случае температурное поле одномерно, а плоские изотермические поверхности располагаются перпендикулярно оси х. Выделим внутри стенки на расстоянии х от поверхности слой толщиной dх, ограниченный двумя изотермическими поверхностями. На основании закона Фурье (уравнение 6) для этого слоя можно написать плотность теплового потока
Разделив переменные, получаем: Интегрирование последнего уравнения дает: Постоянная интегрирования С определяется из граничных условий, а именно: при х =0 t = t1. Подставляя это значение в уравнение (11с), получаем: С = t1 (11д) При х =0 t = t 2, следовательно, Последнее уравнение позволяет определить неизвестную величину плотности теплового потока q, а именно: Следовательно, количество тепла, переданное через 1 м2 стенки в единицу времени с, прямо пропорционально коэффи-циенту теплопроводности λ и разности температур наружных поверхностей стенки Δt и обратно пропорционально толщине стенки δ. При этом следует особо отметить, что тепловой поток определяется не абсолютным значением температур, а их разностью - температурным напором Δt = t 1 - t2. Уравнение (12) является расчетной формулой теплопроводности плоской стенки. Она связывает между собой четыре величины: q, λ, δ и Δt. Зная из них любые три, можно найти четвертую. Отношение Если в уравнение (11с) подставим значение постоянной С из уравнения (11д) и значение q из уравнения (12), то получим уравнение температуры по толщине стенки распределения Последнее является уравнением прямой линии. Следовательно, при постоянном значении коэффициента теплопроводности температура однородной стенки изменяется по закону прямой.
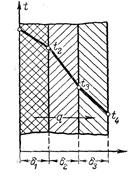
Дополнительные сведения. В действительности же вследствие зависимости от температуры коэффициент теплопроводности является переменной величиной. Если это обстоятельство учесть, то получим иные, более сложные расчетные формулы. Для подавляющего большинства материалов зависимость коэффициента теплопроводности от температуры получается линейной, например λ = λ 0(1 + bt). В этом случае на основании закона Фурье для плоской стенки имеем: Разделив переменные и произведя интегрирование, получим в уравнение (14в) граничные значения переменных, имеем при х = 0 t = t1 и и при х = δ t = t2 и и Вычитая из второго равенства (14с) первое (14д), находим: Откуда Это и есть новая расчетная формула, которая по сравнению с формулой (12) несколько сложнее. В формуле (12) мы принимаем коэффициент теплопроводности постоянным и равным некоторому среднему значению λт. Теперь, приравнивая, правые части формул (12) и (15), имеем: Следовательно, если λт определяется по формуле (6), т. е. по среднеарифметическому из граничных значений температуры стенки, то формулы (12) и (15) равнозначны. Уравнения температурной кривой в стенке получается путем решения квадратного уравнения (14в) относительно t и подставляя значения С из уравнения (14с), а именно: Из этого уравнения следует, что в действительности температура стенки изменяется не по прямой, а по кривой. В некоторых случаях изменение температуры в стенке требуется рассчитывать по этой более сложной формуле (17). Многослойная стенка. Стенки, состоящие из нескольких разнородныхслоев, называются многослойными. Именно такой является кладка металлургических печей, состоящая из огнеупорного и теплоизоляционного материала, а так же обмуровка теплоэнергетических агрегатов. Пусть стенка состоит из нескольких, например трех, разных, но плотно прилегающих друг к другу слоев (рис.7). Толщина первого слоя равна δ 1, второго δ 2 и третьего δ 3 Соответственно коэффициенты теплопроводности слое λ1, λ2 и λ3. Кроме того, известны температуры наружных поверхностей многослойной стенки t 1 и t 2. Благодаря хорошему контакту между слоями соприкасающиеся поверхности имеют одну и ту же температуру, но значения этих температур неизвестны; обозначим их через t 2 и t 3
При стационарном режиме плотность теплового потока постоянна и для всех слоев одинакова. Поэтому на основании формулы (12) для каждого слоя можно написать плотность теплового потока:
Из этих уравнений легко определить изменение температуры в каждом слое:
Сумма изменений температур в каждом слое составляет полный температурный напор. Складывая левые и правые части системы уравнений (в), получим:
Из этого соотношения определяется значение плотности теплового потока:
По аналогии можно сразу записать расчетную формулу для п -слойной стенки:
Так как каждое слагаемое знаменателя в уравнении (19) представляет собой термическое сопротивление слоя, то из уравнения следует, что общее термическое сопротивлением многослойной стенки равно сумме частных термических сопротивлений. Если значение теплового потока из формулы (19) подставить в уравнения (18в), то получим значения неизвестных температур t2 и t3 Внутри каждого слоя температурная кривая изменяется по прямой, но для многослойной стенки в целом она представляет собой ломаную линию (рис.8). Дополнительные сведения. Значения неизвестных температур t2 и t3 можно определить графически.
При этом построение графика производится следующим образом. По оси абсцисс (рис.8) в любом масштабе, но в порядке расположения слоев откладываются значения их термических сопротивлений
Подставляя значения отрезков, получаем: или в соответствии с одним из уравнений (21) Аналогичным образом доказывается, что Иногда ради сокращения выкладок многослойную стенку рассчитывают как однослойную (однородную) стенку толщиной Δ. При этом в расчет вводится так называемый эквивалентный коэффициент теплопроводности, значение которого определяется из следующего соотношения: Отсюда имеем, что Для п -слойной стенки получаем следующую формулу:
Таким образом, эквивалентный коэффициент теплопроводности зависит только от значений термических сопротивлений и толщины отдельных слоев. При выводе формулы для многослойной стенки мы пред- полагали, что слои плотно прилегают друг к другу и благодаря хорошему контакту соприкасающиеся поверхности разных слоев имеют одну и ту же температуру. Однако, если поверхности шероховаты, то тесное соприкосновение невозможно и между слоями образуются тонкие воздушные зазоры. Так как теплопроводность воздуха мала (λ = 0,02), то наличие даже очень тонких зазоров может сильно сказаться в сторону уменьшения эквивалентного коэффициента теплопроводности многослойной стенки. Аналогичное влияние оказывает и слой окисла металла. Поэтому при расчете, и в особенности при измерении теплопроводности многослойной стенки, на плотность контакта между слоями нужно обращать особое внимание. Пример 1-1. Определить часовую потерю тепла через кирпичную стенку длиной 5 м, высотой 3 м и толщиной 250 мм, если на поверхностях поддерживаются температуры t1 = 20°С и t2 = - 30оС. Коэффициент теплопроводности кирпича λ = 0,6 Вт/м К. Согласно уравнениям (1.4) и (1.5) Пример 1-2. Каково значение коэффициента теплопроводности материала стенки, если при δ = 300 мм и Δt = 1000° С, q = 900 Вт/м2 Согласно формуле (1.4) имеем: Пример 1-3. Определить тепловой поток q через плоскую шамотную стенку толщиной δ = 0,5 м и найти действительное распределение температуры, если t1=1 000° С, t2 = 0° С и λ = 1,0 (1+ 0,001 t) Вт/м К Сначала вычислим среднюю температуру стенки tст По этой средней температуре tт определим среднее значение коэффициента теплопроводности λт: λ ст = 1,0(1 +0,001 t ст) = 1,5 Вт/м К. Подставляя полученное значение λ ст в уравнение (12), получим: Точно такой же результат получим и при расчете по формуле (15). Действительное распределение температуры в стенке определяется по уравнению (17). Результаты подсчетов приведены в таблице 2 и на рисунке 3. Для сравнения приведены результаты расчета по формуле (13). Таблица 2 Распределение температур в стенке
ЦИЛИНДРИЧЕСКОЙ СТЕНКИ
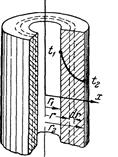
Однородная стенка. Рассмотрим однороднуюцилиндрическую стенку (трубу) длиной l м, с внутренним радиусом r1 и внешним r2. Коэффициент теплопроводности материала постоянен и равен λ. Внутренняя и внешняя поверхности поддерживаются при постоянных температурах t1 и t2, причем t1 > t2, (рис.10). Температура изменяется только в радиальном направлении х.
Следовательно, температурное поле здесь будет одномерным, а изотермические поверхности цилиндрическими поверхностями, имеющими с трубой общую ось. Выделим внутри стенки кольцевой слой с радиусом r и толщиной dr, ограниченный изотермическими поверхностями. Согласно закону Фурье тепловой поток, проходящий через этот слой в сек, равен (Вт) Разделив переменные, получим Интегрирование последнего уравнения дает: Подставляя значение переменных на границах стенки, а именно при r = r 1 и t = t 1 при r = r 2 и t = t 2, получаем следующие два равенства: Вычитая из первого равенства (д) второе (е), находим: откуда определяется неизвестная величина q: Следовательно, тепловой поток через стенку трубы, пря- мо пропорционально коэффициенту теплопроводности λ, длине l и температурному напору Δ t = (t 1 - t 2) и обратно пропорционально натуральному логарифму отношения внешнего радиуса трубы r 2 к внутреннему r 1. Вместо отношения радиусов можно брать отношение диаметров. Уравнение (26) является расчетной формулой теплопроводности цилиндрической стенки. Оно остается справедливым для случая, когда t 1 < t 2, т.е. когда тепловой поток направлен от наружной поверхности к внутренней. Если в уравнение (с) подставить значение постоянной С уравнения (д), а значение Q из уравнения (26), то получим уравнение температурной кривой: Оно представляет собой уравнение логарифмической кривой. Следовательно, внутри однородной цилиндрической стенки постоянном значении коэффициента теплопроводности температура изменяется по логарифмической кривой (рис.10). Дополнительные сведения. Если учесть зависимость коэффициента теплопроводности от температуры λ = λ0(1+ bt), то уравнение температурной кривой для цилиндрической стенки будет иметь следующий вид: Количество тепла, проходящее в час через стенку трубы, может быть отнесено либо к 1 пог. м длины трубопровода, либо к единице внутренней, либо к единице внешней поверхности трубы. При этом расчетные формулы соответственно принимают следующий вид: Так как внутренняя и внешняя поверхности трубы по величине различны, то различными получаются и значения удельных тепловых потоков q1 и q2. Из формул (1.17), (1.18) и (1.19) легко получить соотношение, связывающее между собой величины q 1 и q 2 и q l, а именно: q ·l= π d 1· q 1 = π d 2· q 2
1. 3. 2 Многослойная стенка. Пусть цилиндрическая стенка состоит из нескольких, например трех, разнородных слоев. Благодаря хорошему контакту между слоями соприкасающиеся поверхности разных слоев имеют общую температуру. Диаметры и коэффициенты теплопроводности отдельных слоев известны, их обозначения см. на рис.11. Кроме того, известны температуры внутренней и внешней поверхностей многослойной стенки t 1 и t 4. В местах соприкосновения слоев температуры неизвестны, обозначим их через t 2 и t 3 При стационарном режиме количество тепла, проходящего через каждый слой, одинаково и постоянно. Поэтому на основании формулы (29) можно написать плотность теплового потока
Из этих уравнений определяется изменение температуры в каждом слое: Сумма изменений температуры в каждом слое составляет полный температурный напор. Складывая отдельно левые и правые части системы уравнений (в), получаем:
откуда определяется значение теплового потока ql. По аналогии с этим без вывода можно написать формулу для п -слойной стенки: Если значение ql из формулы (36) подставить в уравнение (33), то получим значения неизвестных температур на поверхности соприкосновения слоев:
Внутри каждого слоя согласно уравнению (27) температура изменяется по логарифмическому закону, но для многослойной стенки в целом температурная кривая представляет собой ломаную кривую (рис.11).
Упрощение расчетных формул (дополнительные сведения). Приведенные выше расчетные формулы для трубы неудобны тем, что в них входит логарифм. С целью упрощения расчетов вместо формулы (29) может быть применена следующая формула теплового потока или плотности теплового потока аналогичная формуле для плоской стенки. Здесь толщина стенки трубы. Влияние кривизны стенки при этом учитывается особым коэффициентом φ, который называется коэффициентом кривизны. Его значение определяется отношением диаметров
Значения коэффициента кривизны для различных отношений приведены на рис. 12.
Рис. 12
приведены на рис.12. Из фигуры видно, что при При расчете теплопроводности многослойной стенки трубы вместо формулы (36) также можно применять упрощенную, которая в этом случае имеет следующий вид: где δi - толщина; dтп - средний диаметр; λ - коэффициент теплопроводности; φ - коэффициент кривизны отдельных слоев много- слойной стенки трубы. ТЕЛ НЕПРАВИЛЬНОЙ ФОРМЫ Каждая из вышеприведенных формул (12а), (26) и (42) применима лишь для одного вида геометрически правильного тела - плоского, цилиндрического или шарового. Расчет тепло-проводности всех этих тел можно охватить одной формулой теплового потока, которая имеет следующий вид: где λ - коэффициент теплопроводности; δ - толщина стенки; Δt - температурный напор; Fх - расчетная поверхность тела. В зависимости от формы тела Fх определяется различно; если F1 - внутренняя и F 2 — внешняя поверхность тела, то: а) для плоской стенки и цилиндрической при б) для цилиндрической стенки при в) для шаровой стенки При расчете теплопроводности плоской стенки, цилиндра и шара формула (44) перед формулами (12), (26) и (42) никаких преимуществ не имеет. Однако ее достоинство заключается в том, что по ней можно рассчитать теплопроводность тел неправильной геометрической формы, например теплопроводность плоской стенки, у которой F1 ≠ F1 т. е. когда поперечное сечение теплового потока в ней представляет собой переменную величину; теплопроводность любых цилиндрических сечений, ограниченных плавными кривыми; теплопроводность всяких замкнутых тел, у которых все три линейных размера между собой близки. В практике нередко встречаются случаи, когда объект расчета является сложным сочетанием различных тел. Расчет теплопроводности таких сложных объектов обычно производят раздельно по элементам, мысленно разрезая их плоскостями параллельно и перпендикулярно направлению теплового потока. Однако вследствие различия термических сопротивлений отдельных элементов, а также вследствие различия их формы в местах соединения элементов распределение температур может иметь очень сложный характер и направление теплового потока может оказаться неожиданным. Поэтому указанный способ расчета сложных объектов имеет лишь приближенный характер. Более точно расчеты сложных объектов можно провести лишь в том случае, если известно распределение изотерм и линий тока, которое можно определить опытным путем при помощи методов гидроэлектроаналогии. Однако самые надежные данные по теплопроводности сложных объектов можно получить только путем непосредственного эксперимента. Опыт можно проводить или на самом объекте, или на уменьшенной модели этого объекта. При выводе расчетных формул принималось, что температуры поверхностей тела постоянны. В практических расчетах это условие не всегда удовлетворяется. В таких случаях поступают следующим образом. Если в отдельных точках поверхности температура разнится не сильно, то производят усреднение температур по поверхности. В дальнейшем с этой средней температурой расчет производится как с постоянной. Средняя температура по поверхности определяется по формуле
где F1, F2, ... , Fп - участки поверхности с постоянной темпе- ратурой; t 1, t 2, ... , tп - температуры этих участков. Если же температура по поверхности изменяется резко, тогда поверхность разбивается на участки и для каждого из них в отдельности подсчитывается количество прошедшего тепла. Складывая эти количества и деля сумму на общую поверхность тела, получают среднее значение теплового потока. В пределах каждого участка усреднение температуры производят по формуле (46). Теплопроводность жидкостных и газовых тел определяется по тем же формулам, какие были приведены для твердых тел. Однако при этом необходимо иметь в виду, что в жидкостях и газах в чистом виде явление теплопроводностди наблюдается лишь в очень тонких слоях и при таком расположении слоя, когда частицы с наименьшей плотностью, т. е. наиболее нагретые, находятся наверху, а наиболее плотные - внизу. В противном случае в слое возникает конвекция, вследствие чего передача тепла через жидкостный или газовый слой возрастает. Кроме того, через газовые слои тепло передается не только путем теплопроводности, но и путем излучения. Все эти обстоятельства сильно затрудняют расчет теплопроводности через газы, и ошибка расчета может достигать 50 - 200%. Поэтому при расчете теплопередачи через газовые прослойки необходимо принимать во внимание и влияние конвекции и излучения.
1.6 НЕСТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ Общие понятия Теплопроводность называется нестационарной, если температурное поле с течением времени изменяется, т. е. происходит нагрев или охлаждение тела. Основное содержание задач нестационарной теплопроводности - отыскание распределения температуры в твердых телах в заданные моменты времени. Все выведенные ниже формулы справедливы как для нагрева, так и для охлаждения тел. Для того, чтобы воспользоваться формулами нестационарной теплопроводности для расчета процесса нагрева или охлаждения необходимо принять по какой модели идет этот процесс – по модели нагрева термически тонкого или термически массивного тела. Для этого рассмотрим критерий Био в формуле термических сопротивлений где α – коэффициент теплоотдачи, Вт/м2 К; S – тепловая толщина, м; l – коэффициент теплопроводности материала, Вт/м К. В соответствии с приведенной зависимостью критерий Био представляет собой отношение внутреннего теплового сопротивления Тела, которые нагреваются (охлаждаются) равномерно по всему объему или разностью температур (например, между поверхностью и центом можно пренебречь), называют термическим тонкими телами, а критерий Вi ≤ 0,25 Тела, для которых критерий Вi ≥ 0,5 и которые нагреваются неравномерно и для которых разностью температур (например, между поверхностью и центом) пренебречь нельзя, называются термически массивными телами. Таким образом, для решения вопроса каким методом проводить расчет нагрева (охлаждения) тела, необходимо вначале вычислить по имеющимся данным критерий Био. Если Вi > 0,5, то расчет необходимо вести по методике термически массивного тела. Если Вi < 0,25, то расчет необходимо вести по методике термически тонкого тела, а так же с использованием критериев. Если Вi находится между 0,25 и 0,5, то такие тема называются телами тяготеющими к термически тонким или термически массивным телам. Таким образом, методику расчета принимают исходя из технологических рекомендаций.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 92; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.186.186 (0.013 с.) |

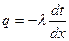 (11а)
(11а)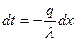 (11в)
(11в)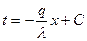 (11с)
(11с)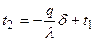 (11е)
(11е)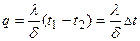 (12)
(12)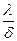 Вт/м2 К называется тепловой проводимостью стенки, а обратная величина
Вт/м2 К называется тепловой проводимостью стенки, а обратная величина 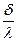 м2 К/ Вт - тепловым или термическим сопротивлением стенки. Последнее определяет падение температуры при прохождении через стенку удельного теплового потока, равного единице. Определив по формуле (12) величину плотности теплового потока, легко вычислить и общее количество тепла Q, переданное через плоскую стенку поверхностью F (м2) в течение времени τ
м2 К/ Вт - тепловым или термическим сопротивлением стенки. Последнее определяет падение температуры при прохождении через стенку удельного теплового потока, равного единице. Определив по формуле (12) величину плотности теплового потока, легко вычислить и общее количество тепла Q, переданное через плоскую стенку поверхностью F (м2) в течение времени τ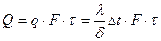 (12а)
(12а)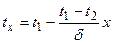 (13)
(13)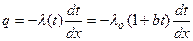 (14а)
(14а)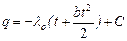 (14в)
(14в)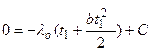 ; (14с)
; (14с)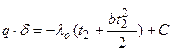 ; (14д)
; (14д) 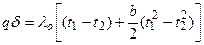 , (14е)
, (14е)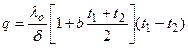 (15)
(15)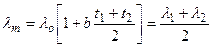 (16)
(16)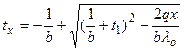 (17)
(17)
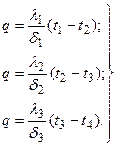 (18а)
(18а)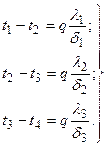 (18в)
(18в)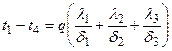 (18с)
(18с)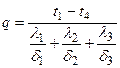 (19)
(19)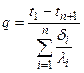 (20)
(20)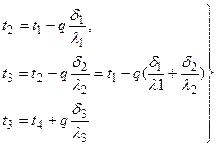
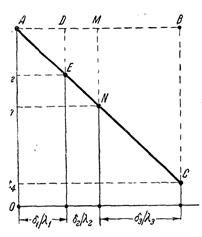
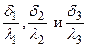 и восстанавливаются перпендикуляры. На крайних из них также в произвольном, но одинаковом масштабе откладываются значения наружных температур t1 и t4. Полученные точки А и С соединяются прямой. Точки пересечения этой прямой со ними перпендикулярами дают значения искомых температур t 2 и t 3. В самом деле, ΔАВС
и восстанавливаются перпендикуляры. На крайних из них также в произвольном, но одинаковом масштабе откладываются значения наружных температур t1 и t4. Полученные точки А и С соединяются прямой. Точки пересечения этой прямой со ними перпендикулярами дают значения искомых температур t 2 и t 3. В самом деле, ΔАВС  ΔАВЕ. Следовательно,
ΔАВЕ. Следовательно,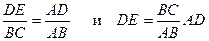
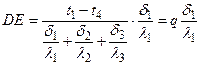
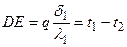
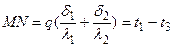
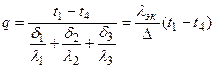 (22)
(22)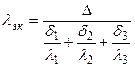 (23)
(23)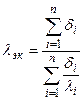 (24)
(24)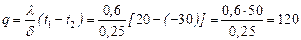 Вт/м2
Вт/м2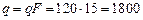 Вт
Вт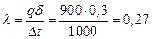
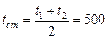 оС
оС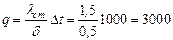 , Вт/м2
, Вт/м2 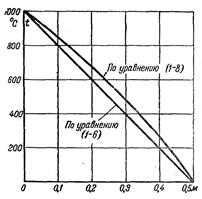
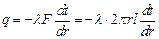 (25а)
(25а) 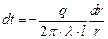 (25в)
(25в) 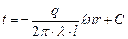 (25с)
(25с) 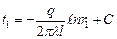 (25д)
(25д)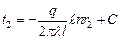 (25е)
(25е)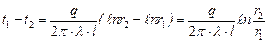
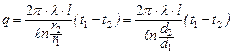 (26)
(26)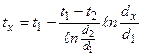 , оС (27)
, оС (27)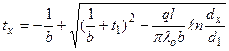 (28)
(28) 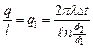 , Вт/м (29)
, Вт/м (29)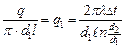 , Вт/м2 (30)
, Вт/м2 (30)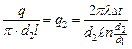 , Вт/м2 (31)
, Вт/м2 (31)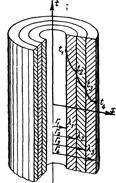
 (32)
(32)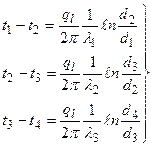 (33)
(33) 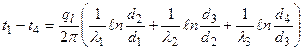 (34)
(34)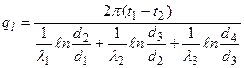 (35)
(35) (36)
(36)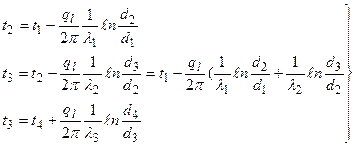 (37)
(37) 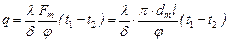
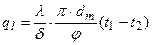 (38)
(38)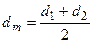 средний диаметр трубы и
средний диаметр трубы и 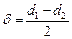 -
-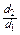 ; в самом деле, из сопоставления между собой формул (29) и (38) имеем:
; в самом деле, из сопоставления между собой формул (29) и (38) имеем: (39)
(39)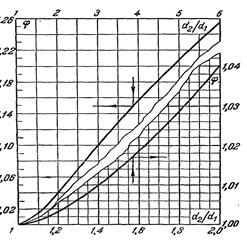
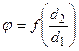
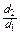 <2 значение φ близко к единице. Так как при φ=1 формула (38) тождественна формуле (12), то это означает, что если толщина стенки трубы по сравнению с диаметром мала или, что то же, если отношение
<2 значение φ близко к единице. Так как при φ=1 формула (38) тождественна формуле (12), то это означает, что если толщина стенки трубы по сравнению с диаметром мала или, что то же, если отношение 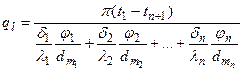 , (40)
, (40)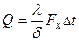 , Вт (44)
, Вт (44) < 2
< 2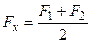 (45а)
(45а) 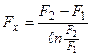 (45в)
(45в) (45с)
(45с)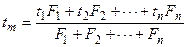 (46)
(46)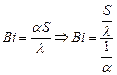 (47)
(47)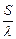 к внешнему
к внешнему  . Чем больше критерий Био, тем больше интенсивность внешнего теплообмена по сравнению с интенсивностью внутреннего. В связи с этим большим значением критерия Био должна соответствовать меньшая равномерность распределения температур в объеме тела, а соответственно большая разница температур, например, между поверхностью и центром заготовки. И наоборот, чем меньше величина критерия Био, тем равномернее распределение температуры в объеме тела на протяжении всего периода нагрева (охлаждения).
. Чем больше критерий Био, тем больше интенсивность внешнего теплообмена по сравнению с интенсивностью внутреннего. В связи с этим большим значением критерия Био должна соответствовать меньшая равномерность распределения температур в объеме тела, а соответственно большая разница температур, например, между поверхностью и центром заготовки. И наоборот, чем меньше величина критерия Био, тем равномернее распределение температуры в объеме тела на протяжении всего периода нагрева (охлаждения).


