
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгебраические дополнения и миноры.Стр 1 из 5Следующая ⇒
Алгебраические дополнения и миноры. (знаю) Обратная матрица. Обратная матрица — такая матрица A−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E: Найдем определитель главной матрицы. Найдем матрицу алгебраических дополнений. Вспоминаем нашу формулу и решим Ранг матрицы. Находим миноры первого порядка, если в матрице есть ненулевые элементы, то её ранг не меньше единицы. Дальше находим минор 3 порядка, 4 и 5. Таким образом, ранг матрицы равен максимальному порядку ненулевого минора. Решение систем уравнений третьего порядка. Правило Крамера. Система линейных уравнений с вещественными коэффициентами:
Определители:
В определителях столбец коэффициентов при соответствующей неизвестной заменяется столбцом свободных членов системы. Решение:
Теорема Крамера. Доказательство. Пусть A - основная матрица системы (4.4), ∆ - ее определитель (главный определитель системы), X - столбец из ее неизвестных и B – столбец свободных членов системы. Тогда уравнение AX = B представляет собой матричную запись системы. Так как по условию теоремы A - невырожденная матрица, то она имеет обратную Умножим обе части равенства
Если в системе
Доказательство. По теореме обратная матрица находится по формуле
где
Заметим, что по формуле (14.13) разложение определителя
Неоднородная система трех линейных уравнений с тремя неизвестными с определителем, равным нулю. Такая система не имеет решений! Однородная система трех линейных уравнений с тремя неизвестными: Совершенно ясно, что однородная система всегда совместна, то есть всегда имеет решение. И, прежде всего, в глаза бросается так называемое тривиальное решение
Векторное произведение двух векторов: выражение векторного произведения в декартовой системе координат.
Смешанное произведение векторов и его свойства.
Смешанное произведение в декартовой системе координат.
Эллипс и его свойства. Эллипс - геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных точек
F1F2=2c По определению эллипса Разделим обе части этого уравнения на
e= называется эксцентриситетом.
X= или - Директриса F1F2=2c – расстояние между фокусами. D= a - ex D1=a + ex – фокальные радиусы
Гипербола и ее свойства.
Свойство 1 Гипербола имеет две взаимно перпендикулярные оси симметрии. Свойство 2 Гипербола имеет центр симметрии.. Центр симметрии гиперболы называют центром гиперболы. Прямые с уравнениями
F1F2=2c – расстояние между фокусами.
X= - Директриса
Парабола и ее свойства. Парабола — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы). Каноническое уравнение параболы в прямоугольной системе координат:
Уравнение директрисы
После возведения в квадрат и некоторых преобразований получается равносильное уравнение
Число p называется фокальным параметром, оно равно расстоянию от фокуса до директрисы Директриса и фокус имеют координаты (-p/2 и p/2).
Эллипс симметричен относительно осей координат Эллипс имеет точки пересечения с осями координат:. Эллипс содержится в прямоугольнике:.
D1=D2=x+p/2
Алгебраические дополнения и миноры. (знаю) Обратная матрица. Обратная матрица — такая матрица A−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E: Найдем определитель главной матрицы. Найдем матрицу алгебраических дополнений. Вспоминаем нашу формулу и решим Ранг матрицы. Находим миноры первого порядка, если в матрице есть ненулевые элементы, то её ранг не меньше единицы. Дальше находим минор 3 порядка, 4 и 5. Таким образом, ранг матрицы равен максимальному порядку ненулевого минора.
|
||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 86; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.86.155 (0.016 с.) |
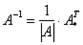
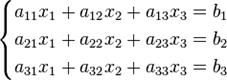



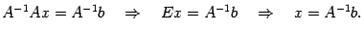
 линейных уравнений с
линейных уравнений с  , то система имеет решение и притом единственное. Это решение задается формулами
, то система имеет решение и притом единственное. Это решение задается формулами

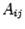 -- алгебраические дополнения. Тогда из (15.3) следует, что
-- алгебраические дополнения. Тогда из (15.3) следует, что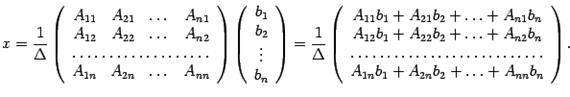
 по первому столбцу в точности совпадает с первым элементом матрицы-столбца в правой части последнего равенства, разложение определителя
по первому столбцу в точности совпадает с первым элементом матрицы-столбца в правой части последнего равенства, разложение определителя 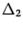 по второму столбцу дает второй элемент матрицы-столбца и т.д. Поэтому
по второму столбцу дает второй элемент матрицы-столбца и т.д. Поэтому 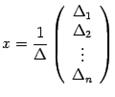 , откуда и следует утверждение теоремы.
, откуда и следует утверждение теоремы.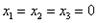 . Так как каждый из определителей имеет столбец, все члены которого равны нулю.
. Так как каждый из определителей имеет столбец, все члены которого равны нулю.




 и
и 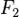 = 2c (называемыхфокусами) постоянна и больше расстояния между фокусами, то есть
= 2c (называемыхфокусами) постоянна и больше расстояния между фокусами, то есть причем
причем 
 . Преобразуем это уравнение:
. Преобразуем это уравнение: 
 получим:
получим: =>
=>  =>
=>  - Каноническое уравнение
- Каноническое уравнение
 коэффициент сжатия эллипса
коэффициент сжатия эллипса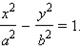 Это уравнение называется каноническим уравнением гиперболы.
Это уравнение называется каноническим уравнением гиперболы. и
и  называются асимптотами гиперболы.
называются асимптотами гиперболы. .
.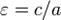 .
.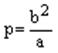 . Фокальный параметр.
. Фокальный параметр. (или
(или  , если поменять местами оси).
, если поменять местами оси).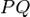 :
:  , фокус —
, фокус — 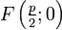 , таким образом начало координат
, таким образом начало координат 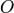 — середина отрезка
— середина отрезка 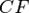 . По определению параболы для любой точки
. По определению параболы для любой точки 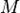 , лежащей на ней выполняется равенство
, лежащей на ней выполняется равенство 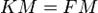 .
. 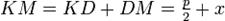 и
и 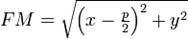 , тогда равенство приобретает вид:
, тогда равенство приобретает вид: 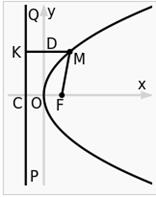
 .
. .
.



