
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема. Каждый вектор X можно представить единственным образом в виде лин. Комбинации векторов базисаСтр 1 из 4Следующая ⇒
Теорема. Каждый вектор x можно представить единственным образом в виде лин.комбинации векторов базиса Пусть Т.е. существуют числа Тогда Это выражение единственно, т.к. если существует другое выражение вычитая из (*) равенство (**), получим Т.к. №3 Теорема. Если Док-во: (1)-лин.независима =>остается док-ть, что для Т.е.векторы Т.о пространство V n-мерно и (1) его базис
№4 Опр. Подмножество L лин. пр-ва V называется лин. подпр. этого пространства если относительно заданных в V операциях (+) и (*а) подпространство L является линейным пространством Теорема Множество L векторов пространства V является лин. подпространством этого пространства ó выполняются (дост) пусть (1) и (2) выполнены, для того что L подпрост.V остается доказать что выполнены все аксиомы лин. пр-ва.
(а-б) и (д-з) вытекает из справедливости для V докажем (в) (необходимость) Пусть L является лин. подпространством этого пространства, тогда (1) и (2) выполняются в силу определения лин. пр-ва Опр. Совокупность всевозможных лин. комбинаций некоторых элементов (xj) лин. пр-ва называется линейной оболочкой Теорема
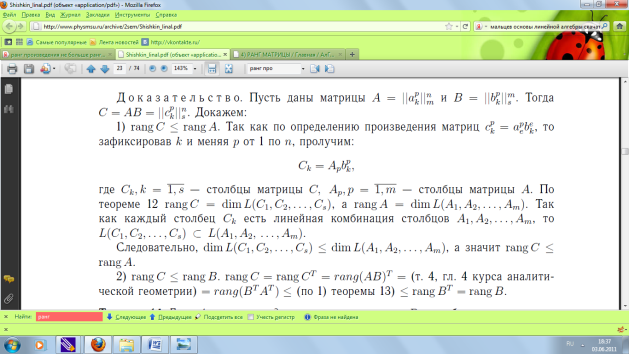
№5 Опр. Непустое подмножество L векторов лин. пр-ва V называется лин. подпространством, если: а)сумма любых векторов из L принадлежит L б)произведение каждого вектора из L на любое число принадлежит L Теорема Ранги эквивалентных систем равны Пусть
№12 Ранг произведения не больше ранга сомножителей
№13 Опр. Два линейных пространстваV1 и V2 называются изоморфными, если между их элементами можно установить взаимно однозначное соответствие, такое что:
(прос-тва над вещ. полем, пр-ва над комплексным) Свойства 1)Если 2) А
Отношение подобия транзитивно 3) каждая матрица подобна самой себе Х=Е. Отношение подобия рефлексивно. Т.о. матрицы одного и того же лин. преобр. всегда подобны
5) Для каждой обратимой A
AB=BA=> 6)
7) №39 Сумма диагональных элементов — следом(trA) | Теорема. Каждый вектор x можно представить единственным образом в виде лин.комбинации векторов базиса Пусть Т.е. существуют числа Тогда Это выражение единственно, т.к. если существует другое выражение вычитая из (*) равенство (**), получим Т.к. №3 Теорема. Если Док-во: (1)-лин.независима =>остается док-ть, что для Т.е.векторы Т.о пространство V n-мерно и (1) его базис
№4 Опр. Подмножество L лин. пр-ва V называется лин. подпр. этого пространства если относительно заданных в V операциях (+) и (*а) подпространство L является линейным пространством Теорема Множество L векторов пространства V является лин. подпространством этого пространства ó выполняются
(дост) пусть (1) и (2) выполнены, для того что L подпрост.V остается доказать что выполнены все аксиомы лин. пр-ва.
(а-б) и (д-з) вытекает из справедливости для V докажем (в) (необходимость) Пусть L является лин. подпространством этого пространства, тогда (1) и (2) выполняются в силу определения лин. пр-ва Опр. Совокупность всевозможных лин. комбинаций некоторых элементов (xj) лин. пр-ва называется линейной оболочкой Теорема
№5 Опр. Непустое подмножество L векторов лин. пр-ва V называется лин. подпространством, если: а)сумма любых векторов из L принадлежит L б)произведение каждого вектора из L на любое число принадлежит L
|
||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 141; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.70.101 (0.021 с.) |
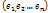 (1) — базис n-мерного лин. пр-ва V, т.е. совокупность линейно независимых векторов. Совокупность векторов
(1) — базис n-мерного лин. пр-ва V, т.е. совокупность линейно независимых векторов. Совокупность векторов 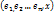 будет лин. зависимой, т.к. их n + 1.
будет лин. зависимой, т.к. их n + 1.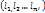 , не все равные нулю одновременно, что
, не все равные нулю одновременно, что 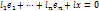 причѐм
причѐм 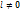 (иначе (1) линейно зависимы).
(иначе (1) линейно зависимы).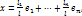 где
где 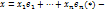 разложение вектора x по базису(1).
разложение вектора x по базису(1).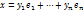 (**)
(**)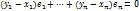
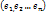 линейно независимы, то
линейно независимы, то  . Чтд
. Чтд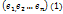 - лин. независимые векторы пространства V и каждый вектор x из V может быть представлен через
- лин. независимые векторы пространства V и каждый вектор x из V может быть представлен через  , то эти векторы образуют базис V
, то эти векторы образуют базис V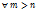
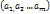 лин.зависимы. По усл. Каждый вектор а выражается через (1):
лин.зависимы. По усл. Каждый вектор а выражается через (1): 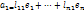 ,
, 
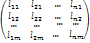 , rang≤n => среди столбцов не больше nлинейно независимы, но m > n=> m столбцов линейно зависимы=>
, rang≤n => среди столбцов не больше nлинейно независимы, но m > n=> m столбцов линейно зависимы=> 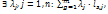 s=1, n
s=1, n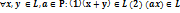
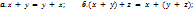
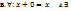 (-x): -x+x=0 д. а(х + у)= ах + ау;
(-x): -x+x=0 д. а(х + у)= ах + ау;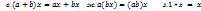
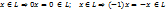
 произвольное множество всех лин. комбинаций векторов V с действ. коэф является лин. подпр V (линейная оболочка данной системы векторов лин. пр. является лин.подпр этого пр.)
произвольное множество всех лин. комбинаций векторов V с действ. коэф является лин. подпр V (линейная оболочка данной системы векторов лин. пр. является лин.подпр этого пр.)
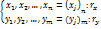
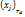 линейно выражается через
линейно выражается через  ,
, 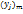 ,
,  , из основной теоремы о линейной зависимости
, из основной теоремы о линейной зависимости 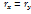
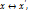

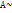 B то В=
B то В= 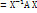 =>
=>  т.о. отношение подобия симметрично
т.о. отношение подобия симметрично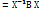 >
> 
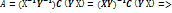
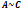


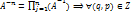
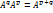
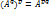
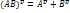
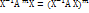 [
[ 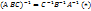 ]
]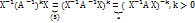
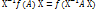
 Опр.
Опр. 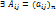 . мат.
. мат. 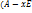 ), где x— незав. переменная, называют характеристической матрицей. Её определитель f(x)=|
), где x— незав. переменная, называют характеристической матрицей. Её определитель f(x)=|  |- характеристическим многочленом оператора А.
|- характеристическим многочленом оператора А.


