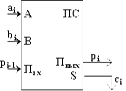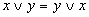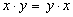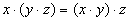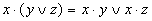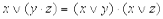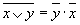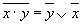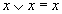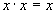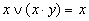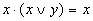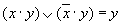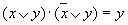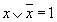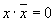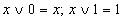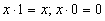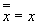Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логические основы компьютераСодержание книги Поиск на нашем сайте
Алгебра логики – это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. Алгебра логики возникла в середине ХIХ века в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами. Логическое высказывание – это любое повествовательное пpедлoжение, в oтнoшении кoтopoгo можно oднoзначнo сказать, истинно оно или лoжнo. Так, например, предложение " 6 – четное число " следует считать высказыванием, так как оно истинное. Предложение " Рим – столица Франции " тоже высказывание, так как оно ложное. Разумеется, не всякое предложение является логическим высказыванием. Высказываниями не являются, например, предложения " ученик десятого класса " и " информатика – интересный предмет ". Первое предложение ничего не утверждает об ученике, а второе использует слишком неопределённое понятие " интересный предмет ". Вопросительные и восклицательные предложения также не являются высказываниями, поскольку говорить об их истинности или ложности не имеет смысла. Предложения типа " в городе A более миллиона жителей ", " у него голубые глаза " не являются высказываниями, так как для выяснения их истинности или ложности нужны дополнительные сведения: о каком конкретно городе или человеке идет речь. Такие предложения называются высказывательными формами. Высказывательная форма – это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями. Алгебра логики рассматривает любое высказывание только с одной точки зрения – является ли оно истинным или ложным. Заметим, что зачастую трудно установить истинность высказывания. Так, например, высказывание " площадь поверхности Индийского океана равна 75 млн кв. км " в одной ситуации можно посчитать ложным, а в другой – истинным. Ложным – так как указанное значение неточное и вообще не является постоянным. Истинным – если рассматривать его как некоторое приближение, приемлемое на практике. Употребляемые в обычной речи слова и словосочетания "не", "и", "или", "если..., то", "тогда и только тогда" и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками. Bысказывания, образованные из других высказываний с помощью логических связок, называются составными. Высказывания, не являющиеся составными, называются элементарными. Так, например, из элементарных высказываний " Петров – врач ", " Петров – шахматист " при помощи связки " и " можно получить составное высказывание " Петров – врач и шахматист ", понимаемое как " Петров – врач, хорошо играющий в шахматы ". При помощи связки " или " из этих же высказываний можно получить составное высказывание " Петров – врач или шахматист ", понимаемое в алгебре логики как " Петров или врач, или шахматист, или и врач и шахматист одновременно ". Истинность или ложность получаемых таким образом составных высказываний зависит от истинности или ложности элементарных высказываний. Чтобы обращаться к логическим высказываниям, им назначают имена. Пусть через А обозначено высказывание "Тимур поедет летом на море", а через В – высказывание "Тимур летом отправится в горы". Тогда составное высказывание "Тимур летом побывает и на море, и в горах" можно кратко записать как А и В. Здесь "и" – логическая связка, А, В – логические переменные, которые могут принимать только два значения – "истина" или "ложь", обозначаемые, соответственно, "1" и "0". Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение: НЕ Операция, выражаемая словом "не", называется отрицанием и обозначается чертой над высказыванием (или знаком Ø). Высказывание И Операция, выражаемая связкой "и" называется конъюнкцией (лат. conjunctio – соединение) или логическим умножением и обозначается точкой" Высказывание АÙВ истинно тогда и только тогда, когда оба высказывания А и В истинны. Например, высказывание "10 делится на 2 и 5 больше 3" истинно, а высказывания "10 делится на 2 и 5 не больше 3", "10 не делится на 2 и 5 больше 3", "10 не делится на 2 и 5 не больше 3" – ложны. ИЛИ Операция, выражаемая связкой "или" (в неисключающем смысле этого слова), называется дизъюнкцией (лат. disjunctio – разделение) или логическим сложением и обозначается знаком Ú (или плюсом). Высказывание А Ú В ложно тогда и только тогда, когда оба высказывания А и В ложны. Например, высказывание "10 не делится на 2 или 5 не больше 3" ложно, а высказывания "10 делится на 2 или 5 больше 3", "10 делится на 2 или 5 не больше 3", "10 не делится на 2 или 5 больше 3" – истинны. ЕСЛИ-ТО Операция, выражаемая связками "если..., то", "из... следует", "... влечет...", называется импликацией (лат. implico – тесно связаны) и обозначается знаком ®. Высказывание A®B ложно тогда и только тогда, когда А истинно, а В ложно. Каким же образом импликация связывает два элементарных высказывания? Покажем это на примере высказываний: "данный четырёхугольник — квадрат" (А) и "около данного четырёхугольника можно описать окружность" (В). Рассмотрим составное высказывание A®B, понимаемое как "если данный четырёхугольник квадрат, то около него можно описать окружность". Есть три варианта, когда высказывание A®B истинно: 1. А истинно и В истинно, то есть данный четырёхугольник квадрат, и около него можно описать окружность; 2. А ложно и В истинно, то есть данный четырёхугольник не является квадратом, но около него можно описать окружность (разумеется, это справедливо не для всякого четырёхугольника); 3. A ложно и B ложно, то есть данный четырёхугольник не является квадратом, и около него нельзя описать окружность. Ложен только один вариант, когда А истинно, а В ложно, то есть данный четырёхугольник является квадратом, но около него нельзя описать окружность. В обычной речи связка "если..., то" описывает причинно-следственную связь между высказываниями. Но в логических операциях смысл высказываний не учитывается. Рассматривается только их истинность или ложность. Поэтому не надо смущаться "бессмысленностью" импликаций, образованных высказываниями, совершенно не связанными по содержанию. Например, такими: "если президент США – демократ, то в Африке водятся жирафы", "если арбуз – ягода, то в бензоколонке есть бензин". РАВНОСИЛЬНО. Операция, выражаемая связками " тогда и только тогда ", " необходимо и достаточно ", "... равносильно...", называется эквиваленцией или двойной импликацией и обозначается знаком Высказывания А и В, образующие составное высказывание Итак, нами рассмотрены пять логических операций: отрицание, конъюнкция, дизъюнкция, импликация и эквиваленция. Импликацию можно выразить через дизъюнкцию и отрицание: Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию: Таким образом, операций отрицания, дизъюнкции и конъюнкции достаточно, чтобы описывать и обрабатывать логические высказывания. Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания ("не"), затем конъюнкция ("и"), после конъюнкции – дизъюнкция ("или") и в последнюю очередь – импликация. С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой. Определение логической формулы: 1. Всякая логическая переменная и символы "истина" ("1") и "ложь" ("0") – формулы. 2. Если А и В – формулы, то Никаких других формул в алгебре логики нет. В качестве примера рассмотрим высказывание "если я куплю яблоки или абрикосы, то приготовлю фруктовый пирог". Это высказывание формализуется в виде Как показывает анализ формулы Некоторые формулы принимают значение "истина" при любых значениях истинности входящих в них переменных. Таковой будет, например, формула В качестве другого примера рассмотрим формулу Если две формулы А и В одновременно, то есть при одинаковых наборах значений входящих в них переменных, принимают одинаковые значения, то они называются равносильными. Равносильность двух формул алгебры логики обозначается символом "=" или символом " Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: “1” и “0”. Из этого следует два вывода: 1. Одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных. 2. На этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера. Данные и команды представляются в виде двоичных последовательностей различной структуры и длины. Существуют различные физические способы кодирования двоичной информации. В электронных устройствах компьютера двоичные единицы чаще всего кодируются более высоким уровнем напряжения, чем двоичные нули (или наоборот), например:
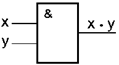
Рисунок 5 – Кодирование информации Логический элемент компьютера – это часть электронной логической схемы, которая реализует элементарную логическую функцию. Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И–НЕ, ИЛИ–НЕ и другие (называемые также вентилями), а также триггер. С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода. Чтобы представить два логических состояния – “1” и “0” в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт. Высокий уровень обычно соответствует значению “истина” (“1”), а низкий – значению “ложь” (“0”). Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем. Работу логических элементов описывают с помощью таблиц истинности. Таблица истинности это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний. Схема И. Схема И реализует конъюнкцию двух или более логических значений. Условное обозначение на структурных схемах схемы И с двумя входами представлено (рисунок 6).
Рисунок 6 – Логический элемент И
Таблица 3. Таблица истинности схемы И
Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль. Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x Схема ИЛИ. Схема ИЛИ реализует дизъюнкцию двух или более логических значений. Когда хотя бы на одном входе схемы ИЛИ будет единица, на её выходе также будет единица. Условное обозначение на структурных схемах схемы ИЛИ с двумя входами. Знак"1"на схеме – от устаревшего обозначения дизъюнкции как ">=1" (т.е. значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1). Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x v y (читается как"x или y") на рисунке 7.
Рисунок 7 – Логический элемент ИЛИ
Таблица 4. Таблица истинности схемы ИЛИ
Схема НЕ. Схема НЕ (инвертор) реализует операцию отрицания. Связь между входом x этой схемы и выходом z можно записать соотношением z= Если на входе схемы 0, то на выходе 1. Когда на входе 1, на выходе 0. Условное обозначение на структурных схемах инвертора – на рисунке 8.
Рисунок 8 – Логический элемент НЕ
Таблица 5. Таблица истинности схемы НЕ
Схема И-НЕ. Схема И-НЕсостоит из элемента Ии инвертора и осуществляет отрицание результата схемы И. Связь между выходом z и входами x и y схемы записывают следующим образом:
Рисунок 9 – Логический элемент И-НЕ
Таблица 6. Таблица истинности схемы И- НЕ
Схема ИЛИ-НЕ. Схема ИЛИ-НЕсостоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ. Связь между выходом z и входами x и y схемы записывают следующим образом:
Рисунок 10 – Логический элемент ИЛИ-НЕ
Таблица 7. Таблица истинности схемы ИЛИ-НЕ
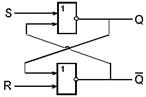
Триггер – это электронная схема, широко применяемая в регистрах компьютера для надёжного запоминания одного разряда двоичного кода. Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое – двоичному нулю. Термин триггерпроисходит от английского слова trigger – защёлка, спусковой крючок. Для обозначения этой схемы в английском языке чаще употребляется термин flip-flop, что в переводе означает “хлопанье”. Это звукоподражательное название электронной схемы указывает на её способность почти мгновенно переходить (“перебрасываться”) из одного электрического состояния в другое и наоборот. Самый распространённый тип триггера – так называемый RS-триггер (S и R, соответственно, от английских set – установка, и reset – сброс). Условное обозначение триггера – на рисунок 11.
Рисунок 11 – Логический элемент RS-триггер
Он имеет два симметричных входа S и R и два симметричных выхода Q и На каждый из двух входов S и R могут подаваться входные сигналы в виде кратковременных импульсов ( Наличие импульса на входе будем считать единицей, а его отсутствие – нулем. На рисунке 12 показана реализация триггера с помощью вентилей ИЛИ-НЕ и соответствующая таблица истинности.
Рисунок 12 – Логический элемент RS-триггер на элементах ИЛИ-НЕ
Таблица 8. Таблица истинности RS-триггер
Проанализируем возможные комбинации значений входов R и S триггера, используя его схему и таблицу истинности схемы ИЛИ-НЕ (таблица 8). 1. Если на входы триггера подать S=“1”, R=“0”, то (независимо от состояния) на выходе Q верхнего вентиля появится “0”. После этого на входах нижнего вентиля окажется R=“0”, Q=“0” и выход 2. Точно так же при подаче “0” на вход S и “1” на вход R на выходе 3. Если на входы R и S подана логическая “1”, то состояние Q и 4. Подача на оба входа R и S логического “0” может привести к неоднозначному результату, поэтому эта комбинация входных сигналов запрещена. Поскольку один триггер может запомнить только один разряд двоичного кода, то для запоминания байта нужно 8 триггеров, для запоминания килобайта, соответственно, 8 Сумматор – это электронная логическая схема, выполняющая суммирование двоичных чисел. Сумматор служит, прежде всего, центральным узлом арифметико-логического устройства компьютера, однако он находит применение также и в других устройствах машины. Многоразрядный двоичный сумматор, предназначенный для сложения многоразрядных двоичных чисел, представляет собой комбинацию одноразрядных сумматоров, с рассмотрения которых мы и начнём. Условное обозначение одноразрядного сумматора на рисунке 13.
Рисунок 13 – одноразрядного сумматора
При сложении чисел A и B в одном i -ом разряде приходится иметь дело с тремя цифрами: - цифра a i первого слагаемого; - цифра b i второго слагаемого; - перенос p i–1 из младшего разряда. В результате сложения получаются две цифры: - цифра c i для суммы; - перенос p i из данного разряда в старший. Таким образом, одноразрядный двоичный сумматор есть устройство с тремя входами и двумя выходами, работа которого может быть описана следующей таблицей истинности (таблица 9). Если требуется складывать двоичные слова длиной два и более бит, то можно использовать последовательное соединение таких сумматоров, причём для двух соседних сумматоров выход переноса одного сумматора является входом для другого. В алгебре логики выполняются следующие основные законы, позволяющие производить тождественные преобразования логических выражений: Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.
Таблица 9. Таблица истинности одноразрядного двоичного сумматора
Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре: (0, 0), (0, 1), (1, 0), (1, 1). Если формула содержит три переменные, то возможных наборов значений переменных восемь: (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1). Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д. Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.
Таблица 10. Основные законы алгебры логики
ЛЕКЦИЯ 6 3.3 Программное обеспечение компьютера Возможности современного ПК столь велики, что все большее число людей находят ему применение в своей работе, учебе, быту. Важнейшим качеством современного компьютера является его "дружественность" по отношению к пользователю. Общение человека с компьютером стало простым, наглядным, понятным. Компьютер сам подсказывает пользователю, что нужно делать в той или иной ситуации, помогает выходить из затруднительных положений. Это возможно благодаря программному обеспечению компьютера. Снова воспользуемся аналогией между компьютером и человеком. Новорожденный человек ничего не знает и не умеет. Знания и умения он приобретает в процессе развития, обучения, накапливая информацию в своей памяти. Компьютер, который собрали на заводе из микросхем, проводов, плат и прочего, подобен новорожденному человеку. Можно сказать, что загрузка в память компьютера программного обеспечения аналогична процессу обучения ребенка. Создается программное обеспечение программистами. Вся совокупность программ, хранящихся на всех устройствах долговременной памяти компьютера, составляет его программное обеспечение(ПО). Программное обеспечение компьютера постоянно пополняется, развивается, совершенствуется. Стоимость установленных программ на современном ПК зачастую превышает стоимость его технических устройств. Разработка современного ПО требует очень высокой квалификации от программистов. Типы программного обеспечения. В программном обеспечении компьютера есть необходимая часть, без которой на нем просто ничего не сделать. Она называется системным ПО. Покупатель приобретает компьютер, оснащенный системным программным обеспечением, которое не менее важно для работы компьютера, чем память или процессор. Кроме системного ПО в состав программного обеспечения компьютера входят еще прикладные программы и системы программирования. Программное обеспечение компьютера делится на: - системное ПО; - прикладное ПО; - системы программирования. О системном ПО и системах программирования речь пойдет позже. А сейчас познакомимся с прикладным программным обеспечением. Состав прикладного программного обеспечения. Программы, с помощью которых пользователь может решать свои информационные задачи, не прибегая к программированию, называются прикладными программами. Как правило, все пользователи предпочитают иметь набор прикладных программ, который нужен практически каждому. Их называют программами общего назначения. К их числу относятся: - текстовые и графические редакторы, с помощью которых можно готовить различные тексты, создавать рисунки, строить чертежи; проще говоря, писать, чертить, рисовать; - системы управления базами данных (СУБД), позволяющие превратить компьютер в справочник по любой теме; - табличные процессоры, позволяющие организовывать очень распространенные на практике табличные расчеты; - коммуникационные (сетевые) программы, предназначенные для обмена информацией с другими компьютерами, объединенными с данным в компьютерную сеть. Очень популярным видом прикладного программного обеспечения являются компьютерные игры. Большинство пользователей именно с них начинает свое общение с ЭВМ. Кроме того, имеется большое количество прикладных программ специального назначениядля профессиональной деятельности. Их часто называют пакетами прикладных программ. Это, например, бухгалтерские программы, производящие начисления заработной платы и другие расчеты, которые делаются в бухгалтериях; системы автоматизированного проектирования, которые помогают конструкторам разрабатывать проекты различных технических устройств; пакеты, позволяющие решать сложные математические задачи без составления программ; обучающие программы по разным школьным предметам и многое другое. Главной частью системного программного обеспечения является операционная система (ОС). Операционная система - это набор программ, управляющих оперативной памятью, процессором, внешними устройствами и файлами, ведущих диалог с пользователем. У операционной системы очень много работы, и она практически все время находится в рабочем состоянии. Например, для того чтобы выполнить прикладную программу, ее нужно разыскать во внешней памяти (на диске), поместить в оперативную память, найдя там свободное место, "запустить" процессор на выполнение программы, контролировать работу всех устройств машины во время выполнения и в случае сбоев выводить диагностические сообщения. Все эти заботы берет на себя операционная система. Все программы и данные хранятся в долговременной (внешней) памяти компьютера в виде файлов. Файл – это определенное количество информации (программа или данные), имеющее имя и хранящееся в долговременной (внешней) памяти. Имя файла состоит из двух частей, разделенных точкой: собственно имя файла и расширение, определяющее его тип (программа, данные и т. д.). Собственно имя файлу дает пользователь, а тип файла обычно задается программой автоматически при его создании.
Таблица 11. Соответствие типа файла и расширения
В различных операционных системах существуют различные форматы имен файлов. В операционной системе MS-DOS собственно имя файла должно содержать не более восьми букв латинского алфавита и цифр, а расширение состоит из трех латинских букв, например: proba.txt В операционной системе Windows имя файла может иметь до 255 символов, причем допускается использование русского алфавита, например: Единицы измерения информации.doc До появления операционной системы Windows 95 на большинстве компьютеров IBM PC работала операционная система MS-DOS, в которой действовали весьма строгие правила присвоения имен файлам. Эти правила называют соглашением 8.3 По соглашению 8.3 имя файла может состоять из двух частей, разделенных точкой. Первая часть может иметь длину до 8 символов, а вторая часть (после точки) – до 3 символов. Вторая часть, стоящая после точки, называется расширением имени. При записи имени файла разрешается использовать только буквы английского алфавита и цифры. Начинаться имя должно с буквы. Пробелы и знаки препинания не допускаются, за исключением восклицательного знака (!), тильды (~) и символа подчеркивания (_). После введения в действие операционной системы Windows 95 требования к именам файлов стали существенно мягче. Они действуют и во всех последующих версия операционных систем Windows. 1. Разрешается использовать до 255 символов. 2. Разрешается использовать символы национальных алфавитов, в частности русского. 3. Разрешается использовать пробелы и другие, ранее запрещенные символы, за исключением следующих девяти: /\:*?"<>|. 4. В имени файла можно использовать несколько точек. Расширением имени считаются все символы, стоящие за последней точкой. Роль расширения имени файла чисто информационная, а не командная. Если файлу с рисунком присвоить расширение имени ТХТ, то содержимое файла от этого не превратится в текст. Его можно просмотреть в программе, предназначенной для работы с текстами, но ничего вразумительного такой просмотр не даст. Файловая система. На каждом носителе информации (гибком, жестком или лазерном диске) может храниться большое количество файлов. Порядок хранения файлов на диске определяется установленной файловой системой. Файловая система – это система хранения файлов и организации каталогов. Для дисков с небольшим количеством файлов (до нескольких десятков) удобно применять одноуровневую файловую систему, когда каталог (оглавление диска) представляет собой линейную последовательность имен файлов (рисунок 14). Для отыскания файла на диске достаточно указать лишь имя файла.
Рисунок 14 – Корневой каталог с файлами
Если на диске хранятся сотни и тысячи файлов, то для удобства поиска файлы организуются в многоуровневую иерархическую файловую систему, которая имеет «древовидную» структур
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 130; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.37.211 (0.014 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 истинно, когда A ложно, и ложно, когда A истинно. Пример. " Луна – спутник Земли " (А); " Луна – не спутник Земли " (
истинно, когда A ложно, и ложно, когда A истинно. Пример. " Луна – спутник Земли " (А); " Луна – не спутник Земли " ( " (может также обозначаться знаками Ù или &).
" (может также обозначаться знаками Ù или &).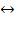 или
или  Высказывание
Высказывание 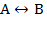 истинно тогда и только тогда, когда значения А и В совпадают. Например, высказывания "24 делится на 6 тогда и только тогда, когда 24 делится на 3", "23 делится на 6 тогда и только тогда, когда 23 делится на 3" истинны, а высказывания "24 делится на 6 тогда и только тогда, когда 24 делится на 5", "21 делится на 6 тогда и только тогда, когда 21 делится на 3" ложны.
истинно тогда и только тогда, когда значения А и В совпадают. Например, высказывания "24 делится на 6 тогда и только тогда, когда 24 делится на 3", "23 делится на 6 тогда и только тогда, когда 23 делится на 3" истинны, а высказывания "24 делится на 6 тогда и только тогда, когда 24 делится на 5", "21 делится на 6 тогда и только тогда, когда 21 делится на 3" ложны.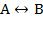 , могут быть совершенно не связаны по содержанию, например: "три больше двух" (А), "пингвины живут в Антарктиде" (В). Отрицаниями этих высказываний являются высказывания "три не больше двух" (
, могут быть совершенно не связаны по содержанию, например: "три больше двух" (А), "пингвины живут в Антарктиде" (В). Отрицаниями этих высказываний являются высказывания "три не больше двух" ( ). Образованные из высказываний А и В составные высказывания
). Образованные из высказываний А и В составные высказывания 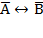 истинны, а высказывания
истинны, а высказывания 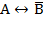 и
и 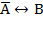 – ложны.
– ложны.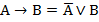 .
.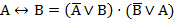 .
.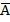 , А
, А 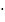 В, А
В, А 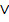 В, А
В, А  B, А
B, А  В – формулы.
В – формулы. . Такая же формула соответствует высказыванию "если Игорь знает английский или японский язык, то он получит место переводчика".
. Такая же формула соответствует высказыванию "если Игорь знает английский или японский язык, то он получит место переводчика".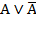 , соответствующая высказыванию "Этот треугольник прямоугольный или косоугольный". Эта формула истинна и тогда, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный. Такие формулы называются тождественно истинными формулами или тавтологиями. Высказывания, которые формализуются тавтологиями, называются логически истинными высказываниями.
, соответствующая высказыванию "Этот треугольник прямоугольный или косоугольный". Эта формула истинна и тогда, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный. Такие формулы называются тождественно истинными формулами или тавтологиями. Высказывания, которые формализуются тавтологиями, называются логически истинными высказываниями.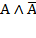 , которой соответствует, например, высказывание "Катя самая высокая девочка в классе, и в классе есть девочки выше Кати". Очевидно, что эта формула ложна, так как либо А, либо
, которой соответствует, например, высказывание "Катя самая высокая девочка в классе, и в классе есть девочки выше Кати". Очевидно, что эта формула ложна, так как либо А, либо  " Замена формулы другой, ей равносильной, называется равносильным преобразованием данной формулы.
" Замена формулы другой, ей равносильной, называется равносильным преобразованием данной формулы.

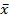 , x где
, x где 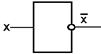
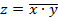 , где
, где  читается как "инверсия x и y". Условное обозначение на структурных схемах схемы И-НЕ с двумя входами представлено на рисунке 9.
читается как "инверсия x и y". Условное обозначение на структурных схемах схемы И-НЕ с двумя входами представлено на рисунке 9.
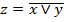 , где
, где 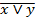 , читается как "инверсия x или y". Условное обозначение на структурных схемах схемы ИЛИ-НЕ с двумя входами представлено на рисунке 10.
, читается как "инверсия x или y". Условное обозначение на структурных схемах схемы ИЛИ-НЕ с двумя входами представлено на рисунке 10.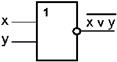

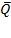 , причем выходной сигнал Q является логическим отрицанием сигнала
, причем выходной сигнал Q является логическим отрицанием сигнала  ).
).
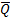
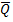 появится “0”, а на Q – “1”.
появится “0”, а на Q – “1”.