Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимальный модель посудомоечная машинаСодержание книги
Поиск на нашем сайте
Проблема нормализации локальных критериев возникает во всех задачах векторной оптимизации, когда локальные критерии имеют различные единицы измерения. В основу нормализации положено понятие «идеального вектора», т.е. вектора с идеальными значениями локальных критериев
В нормализованном пространстве критериев вместо действительного значения локального критерия
действительная величина, поделенная на идеальную величину. В том случае, если лучшим считается большее значение критерия и если способ. Идеальный вектор определяется некоторыми заданными значениями локальных критериев. Эти заданные значения может определить, например, заказчик разработки. Формальная запись:
Недостаток этого способа - полнейший субъективизм выбора. способ. Идеальным считается вектор, параметрами которого являются максимально возможные значения локальных критериев:
способ. В качестве параметров идеального вектора принимается максимально возможный разброс значений, соответствующих локальных критериев, т.е.
Необходимо отметить, что нет формальных способов по выбору способа задания идеального вектора. Проведем нормализацию данных, воспользовавшись 2-ым способом из предложенных трех - выберем в каждом столбце максимальное значение и разделим на это число все элементы столбца.
Для 1-го критерия:
Остальные рассчитываются по такому же принципу. Получим:
Таблица 2
Свертка локальных критериев
Локальные критерии f1 и f2 необходимо максимизировать, а f3, f4 и f5 - минимизировать, поэтому необходимо произвести свертку. Свертка подразумевает возведение в степень (-1) тех локальных критериев, которые необходимо минимизировать (у нас это f3, f4 и f5). Получим:
Таблица 3
Пункт А - сравнение без учета приоритетов локальных критериев Рассмотрим основные схемы компромиссов, когда все локальные критерии нормализованы, то есть все имеют одинаковую размерность либо являются безразмерными величинами. Кроме того, все локальные критерии имеют одинаковую важность, и лучшим будем считать большее значение локального критерия. Принцип равномерности
Он провозглашает целесообразным выбор такого варианта решения, принадлежащего области компромиссов, при котором достигалась бы некоторая равномерность показателей по всем локальным критериям. Используются следующие реализации принципа равномерности: а) принцип равенства, б) принцип квазиравенства, в) принцип максимина. Принцип равенства Он провозглашает целесообразность выбора такого варианта, при котором все значения локальных критериев равны между собой. Например, если бы было f21 = f22 = f23. Остальные значения не равны между собой. Тогда вариант 2 был бы лучшим. Эта модель расписывается следующим образом:
x⊂WFk
В данном случае принцип равенства не работает. Принцип квазиравенства Практически достичь равенства локальных критериев не удается, тогда лучшим признается вариант, в котором локальные критерии более близки к этому равенству. В нашем случае принцип квазиравенства работает в варианте №1 Принцип максимина Для каждого варианта выбирается минимальное значение локального критерия, и окончательный выбор останавливается на варианте, в котором этот минимум достигает своего максимума. В этом случае равномерность обеспечивается за счет подтягивания локального критерия с наименьшим значением показателя. Max min(1, 0.5, 1, 0.67, 0.75)=1 => оптимальными признаются варианты №1 и №3. После рассмотрения принципа равномерности мы получили: ) принцип равенства не работает; ) принцип квазиравенства признает оптимальным вариант №1; ) принцип максимина признает оптимальными варианты №1 и №3.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-27; просмотров: 200; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.40.134 (0.009 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

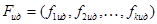
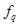 рассматривается безразмерная величина
рассматривается безразмерная величина 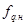 :
: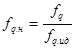
 , то
, то 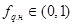 . Успешное решение проблемы нормализации во многом определяется тем, насколько удачен окажется выбор параметров идеального вектора. Существует три основных способа задания идеального вектора.
. Успешное решение проблемы нормализации во многом определяется тем, насколько удачен окажется выбор параметров идеального вектора. Существует три основных способа задания идеального вектора.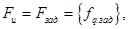
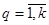 .
. ,
, 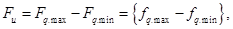
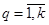
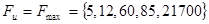
 - вектор идеальных значений
- вектор идеальных значений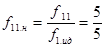 ,
, 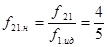 ,
, 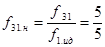 ,
, 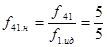 ,
,