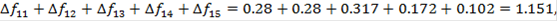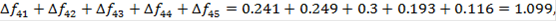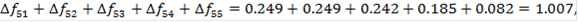Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормализация локальных критериевСтр 1 из 5Следующая ⇒
Задание
Используя известные схемы компромиссов, определить лучший вариант по 5-ти локальным критериям: А - без учета приоритетов локальных критериев; В - с учетом приоритетов локальных критериев. Предметная область состоит из множества различных моделей посудомоечных машин. Элементы предметной области обладают следующими характеристиками: габариты; установка; возможность подключения к горячей воде; объем памяти; вместимость; класс мойки; сушка; класс энергопотребления; защита от протечек; уровень шума; таймер отсрочки запуска; защита от детей; цена и т. д. Необходимо выбрать оптимальный вариант из 5-ти моделей посудомоечных машин производства компании Bosh: - Bosh SMV 50E50 - 1; Bosh SKS 40E02 - 2; Bosh SRS 55M76 - 3; Bosh SCE 53M25 - 4; Bosh SRS 46T22- 5; с учетом 5-ти локальных критериев: ) Количество программ - f1 - максимизировать; ) Количество загружаемых комплектов - f2 - максимизировать; ) глубина (мм) (т. к. место, где планируется разместить машину, ограничено) - f3 - минимизировать; ) высота (мм) - f4 - минимизировать; ) цена (руб.) - f5 - минимизировать; Решение Данная задача относится к классу многокритериальных задач принятия решений, в котором принимаемое решение описывается совокупностью критериев:
Кроме того, каждый из этих критериев характеризуется своим коэффициентом относительной важности:
т. е. мы можем сказать, что совокупность локальных или частных критериев
F= {
В свою очередь коэффициенты относительной важности
В нашем задании в пункте А приоритет локальных критериев учитываться не будет, а в пункте В - будет. Задача заключается в том, чтобы найти оптимальное значение Каждый локальный критерий характеризует одно какое-либо качество принимаемого решения (разрешение, стоимость, скорость печати и т. д.) Совокупность этих локальных критериев образует интегральный критерий, различный для каждого типа машины. И с помощью интегрального критерия можно проводить сравнения различных типов принтеров или качества принимаемого решения.
Формально оптимальное решение
x∈
В этом соотношении, вернее в этой формальной записи критерия оптимальности, Область допустимых значений ) ) Таким образом, первый этап принятия решения - это разбиение области допустимых значений на область согласия и область компромиссов. Это разбиение позволяет существенно сократить число рассматриваемых вариантов. Далее необходимо задаться некоторой схемой компромисса, или, иначе говоря, раскрыть смысл оператора opt в выражении (1). В дальнейшем нам будет удобнее от допустимого пространства управляющей воздействий
Представим наши данные в виде таблицы:
Свертка локальных критериев
Локальные критерии f1 и f2 необходимо максимизировать, а f3, f4 и f5 - минимизировать, поэтому необходимо произвести свертку. Свертка подразумевает возведение в степень (-1) тех локальных критериев, которые необходимо минимизировать (у нас это f3, f4 и f5).
Получим:
Таблица 3
Принцип равномерности
Он провозглашает целесообразным выбор такого варианта решения, принадлежащего области компромиссов, при котором достигалась бы некоторая равномерность показателей по всем локальным критериям. Используются следующие реализации принципа равномерности: а) принцип равенства, б) принцип квазиравенства, в) принцип максимина. Принцип равенства Он провозглашает целесообразность выбора такого варианта, при котором все значения локальных критериев равны между собой. Например, если бы было f21 = f22 = f23. Остальные значения не равны между собой. Тогда вариант 2 был бы лучшим. Эта модель расписывается следующим образом:
x⊂WFk
В данном случае принцип равенства не работает. Принцип квазиравенства Практически достичь равенства локальных критериев не удается, тогда лучшим признается вариант, в котором локальные критерии более близки к этому равенству. В нашем случае принцип квазиравенства работает в варианте №1 Принцип максимина Для каждого варианта выбирается минимальное значение локального критерия, и окончательный выбор останавливается на варианте, в котором этот минимум достигает своего максимума. В этом случае равномерность обеспечивается за счет подтягивания локального критерия с наименьшим значением показателя. Max min(1, 0.5, 1, 0.67, 0.75)=1 => оптимальными признаются варианты №1 и №3. После рассмотрения принципа равномерности мы получили: ) принцип равенства не работает; ) принцип квазиравенства признает оптимальным вариант №1; ) принцип максимина признает оптимальными варианты №1 и №3.
Вывод После рассмотрения принципа выделения одного оптимизируемого критерия мы получили, что наилучшими будут варианты №1 и №2. Вывод После рассмотрения принципа последовательной уступки мы получили, что наилучшим является вариант №4. Принцип равномерности Он провозглашает целесообразный выбор такого варианта решения, принадлежащего области компромиссов, при котором достигалась бы некоторая равномерность показателей по всем локальным критериям. Используя следующие реализации принципа равномерности: А) Принцип равенства. Б) Принцип квазиравенства. В) Принцип максимина. Принцип равенства
Он провозглашает целесообразность выбора такого варианта, при котором все значения локальных критериев равны между собой. В данном случае принцип равенства не работает. Принцип квазиравенства
Практически достичь равенства локальных критериев не удаётся, тогда лучшим признаётся вариант, в котором локальные критерии более близки к этому равенству. В нашем случае принцип квазиравенства не работает. Принцип максимина
Для каждого варианта выбирается минимальное значение локального критерия, и окончательный выбор останавливается на варианте, в котором этот минимум достигает своего максимума. В этом случае равномерность обеспечивается за счёт подтягивания локального критерия с наименьшим значением показателя. Max (0,102; 0,102; 0,08; 0,116; 0,082) = 0,116 => оптимальным признаётся вариант №4
Вывод После рассмотрения принципа равномерности мы получили: ) принцип равенства не работает; ) принцип квазиравентсва не работает; ) принцип максимина признаёт оптимальными вариант №4.
Принцип абсолютной уступки
Лучшим по принципу абсолютной уступки считается компромисс, при котором абсолютное значение суммы снижения одного или нескольких критериев не превышает абсолютного значения суммы приращений оставшихся критериев. а) первый способ Смотрим на нашу таблицу 4 и сравниваем между собой первый и второй варианты. При переходе от первого варианта ко второму мы имеем: ∆f1 - приращение первого критерия. ∆f1 = f21 - f11 = 0,28 - 0,28 = 0. Сравниваем эти два варианта по второму критерию: ∆f2 = f22 - f12 = 0,28 - 0,28 = 0. Сравниваем между собой эти два варианта по третьему критерию: ∆f3 = f23 - f13 = 0,266 - 0,317 = -0,051 < 0. Сравниваем между собой эти два варианта по четвёртому критерию: ∆f4 = f24 - f14 = 0,12 - 0,172 = -0,052 < 0. Сравниваем между собой эти два варианта по пятому критерию: ∆f5 = f25 - f15 = 0,102 - 0,102 = 0. ∆f1, ∆f2 и ∆f5 не дают не проигрыша, ни выигрыша, а ∆f3 и ∆f4 - проигрышны. Таким образом, переход к варианту 2 не осуществляется -вариант 2 отбрасывается, а сравнение ведётся с выбранным вариантом и следующим по порядку вариантом. То есть, теперь сравним по той же схеме первый и третий варианты:
∆f1 = f31 - f11 = 0,232 - 0,28 = -0,048 < 0. ∆f2 = f32 - f12 = 0,238 - 0,28 = -0,042 < 0. ∆f3 = f33 - f13 = 0,24 - 0,317 = -0,077 < 0. ∆f4 = f34 - f14 = 0,272 - 0,172 = 0,1 > 0. ∆f5 = f35 - f15 = 0,08 - 0,102 = -0,022 < 0. ∆f4 - выигрыша, а ∆f1, ∆f2, ∆f3 и ∆f5 - проигрышна. |∆f4|<|∆f1+∆f2+∆f3+∆f5| ,1 < 0,189
Опять-таки переход к варианту 3 не осуществляется - вариант 3 отбрасывается, а сравнение ведётся первого и четвёртого вариантов:
∆f1 = f41 - f11 = 0,241 - 0,28 = -0,039 < 0. ∆f2 = f42 - f12 = 0,249 - 0,28 = -0,031 < 0. ∆f3 = f43 - f13 = 0,3 - 0,317 = -0,017 < 0.
Переход к варианту 4 не осуществляется - вариант 4 отбрасывается, и сравнение ведется первого и пятого вариантов:
Таким образом, переход к варианту 5 не осуществляется - вариант 5 отбрасывается, а т.к. все варианты просмотрены, оптимальным признается вариант №1. б) второй способ Принципу абсолютной уступки также соответствует модель максимизации суммы локальных критериев:
т.е. ищется сумма по строкам всех локальных критериев:
И та из этих сумм, которая окажется максимальной, соответствует лучшему варианту. В данном случае максимальная сумма 1,151 соответствует варианту №1, который и признается лучшим. Вывод После рассмотрения принципа одного оптимизируемого критерия, мы получили, что наилучшими вариантами являются №1 и №2.
Вывод
Пункт А После анализа результатов по всем применённым критериям, оптимальными могут быть признаны варианты №1 и №2. Пункт В После анализа результатов по всем применённым критериям, оптимальным может быть признан вариант №1. Задание
Используя известные схемы компромиссов, определить лучший вариант по 5-ти локальным критериям: А - без учета приоритетов локальных критериев; В - с учетом приоритетов локальных критериев. Предметная область состоит из множества различных моделей посудомоечных машин. Элементы предметной области обладают следующими характеристиками: габариты; установка; возможность подключения к горячей воде; объем памяти; вместимость; класс мойки; сушка; класс энергопотребления; защита от протечек; уровень шума; таймер отсрочки запуска; защита от детей; цена и т. д. Необходимо выбрать оптимальный вариант из 5-ти моделей посудомоечных машин производства компании Bosh: - Bosh SMV 50E50 - 1; Bosh SKS 40E02 - 2; Bosh SRS 55M76 - 3; Bosh SCE 53M25 - 4; Bosh SRS 46T22- 5; с учетом 5-ти локальных критериев: ) Количество программ - f1 - максимизировать; ) Количество загружаемых комплектов - f2 - максимизировать; ) глубина (мм) (т. к. место, где планируется разместить машину, ограничено) - f3 - минимизировать; ) высота (мм) - f4 - минимизировать; ) цена (руб.) - f5 - минимизировать; Решение Данная задача относится к классу многокритериальных задач принятия решений, в котором принимаемое решение описывается совокупностью критериев:
Кроме того, каждый из этих критериев характеризуется своим коэффициентом относительной важности:
т. е. мы можем сказать, что совокупность локальных или частных критериев
F= {
В свою очередь коэффициенты относительной важности
В нашем задании в пункте А приоритет локальных критериев учитываться не будет, а в пункте В - будет. Задача заключается в том, чтобы найти оптимальное значение Каждый локальный критерий характеризует одно какое-либо качество принимаемого решения (разрешение, стоимость, скорость печати и т. д.) Совокупность этих локальных критериев образует интегральный критерий, различный для каждого типа машины. И с помощью интегрального критерия можно проводить сравнения различных типов принтеров или качества принимаемого решения.
Формально оптимальное решение
x∈
В этом соотношении, вернее в этой формальной записи критерия оптимальности, Область допустимых значений ) ) Таким образом, первый этап принятия решения - это разбиение области допустимых значений на область согласия и область компромиссов. Это разбиение позволяет существенно сократить число рассматриваемых вариантов. Далее необходимо задаться некоторой схемой компромисса, или, иначе говоря, раскрыть смысл оператора opt в выражении (1). В дальнейшем нам будет удобнее от допустимого пространства управляющей воздействий
Представим наши данные в виде таблицы:
Нормализация локальных критериев
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-27; просмотров: 245; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.243.32 (0.134 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
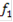
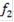
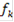
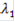
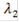
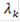
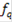
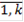
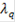

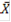
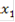
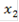
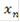
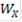

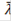

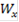
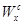 - область, в которой качество принимаемого решения может быть улучшено по одному или нескольким локальным критериям без ухудшения хотя бы одного из оставшихся локальных критериев;
- область, в которой качество принимаемого решения может быть улучшено по одному или нескольким локальным критериям без ухудшения хотя бы одного из оставшихся локальных критериев;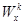 - область компромиссов, в которой улучшение решений по одному или нескольким локальным критериям обязательно приводит к снижению значения одного или нескольких оставшихся критериев. В этом случае для того, чтобы выбрать окончательно какой-либо вариант, мы должны найти некоторый компромисс, поэтому говорят, что эти два варианта лежат в области компромисса.
- область компромиссов, в которой улучшение решений по одному или нескольким локальным критериям обязательно приводит к снижению значения одного или нескольких оставшихся критериев. В этом случае для того, чтобы выбрать окончательно какой-либо вариант, мы должны найти некоторый компромисс, поэтому говорят, что эти два варианта лежат в области компромисса.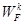 , тогда расписанная выше модель может быть формализована следующим образом, то есть
, тогда расписанная выше модель может быть формализована следующим образом, то есть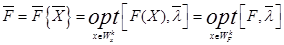 (2)
(2)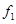
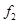
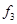
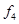
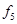
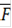


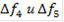
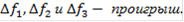
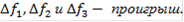
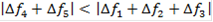
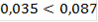


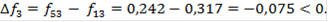

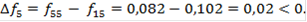
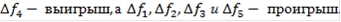
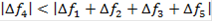
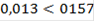
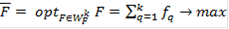
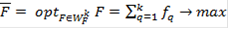 ,
,