
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Побудова моделей для прогнозування витрат виробництваСодержание книги
Поиск на нашем сайте
Для аналізу витрат виробництва необхідно побудувати три моделі: ) модель, що відображає залежність собівартості одиниці товару від обсягу виробництва; ) модель, що відображає залежність загальної собівартості від обсягу виробництва; ) модель, що відображає залежність обсягів виробництва від витрат виробництва (витрат капіталу та праці). Побудуємо три типи моделей. Модель, що відображає залежність собівартості одиниці продукції від обсягу виробництва. Першим кроком при побудові економетричної моделі 1 є аналіз спостережень та вибір виду функції для побудови моделі. Графічне зображення спостережень наведено на рис. 3.1 і в табл. 3.1
Таблиця 3.1 - Початкові дані для побудови моделі
Рисунок 3.1 - Залежність собівартості від обсягу виробництва
Аналізуючи дані табл. 3.1 та рис. 3.1 можна зробити висновок, що між собівартістю та обсягом виробництва існує гіперболічна залежність, яка має наступний вигляд
де а0, а1 - параметри моделі;- собівартість одиниці продукції Т-150К, у - обсяг виробництва цієї продукції. Дані для розрахунку цієї моделі наведено в табл. 3.1. Наступним етап для побудови економетричної моделі є знаходження параметрів моделі і перевірка їх статистичної значущості. Знаходження параметрів моделі здійснюється за допомогою МНК. Перевірка статистичної стачущості - за допомогою критерія Ст’юдента. Застосувавши для розрахунків програму Statistica, визначимо параметри моделі. Розрахунок параметрів наведенов табл. 3.2
Таблиця 3.2 - Розрахунок параметрів моделі
Аналіз значень критерію Ст’юдента дозволяє зробити висновок, що параметри моделі a0 та a1 є значущими. Таким чином модель має вигляд:
Третім етапом побудови моделі є перевірка адекватності моделі. Перевірка адекватності здійснюється за допомогою коефіцієнту множинної кореляції, що розраховується за наступною формулою:
Даний коефіцієнт також розраховувався за допомогою ПП Statistica. Він дорівнює 0,999. Таким чином, побудовану модель можна використовувати для прогнозування собівартості одиниці продукції в залежності від обсягу виробництва. Проведемо аналіз коефіцієнтів даної моделі. Так як ми прогнозуємо собівартість на одиницю продукцїї, то при збільшенні обсягу виробництва постійні витрати на одиницю продукцї будуть зменшуватись, тобто коефіцієнт а1 буде характеризувати постійні витрати за кінцевий період часу, а співвідношення Модель, що відображає залежність загальної собівартості від обсягу виробництва; Дані для побудови моделі наведено у табл. 3.3 та на рис. 3.2. Дані наведені в табл. 3.3 та сображені на рис. 3.2 свідчать, що між загальною собівартістю та обсягом виробництва існує лінійний зв’язок,
Таблиця 3.3 - Початкові дані
Тобто модель можна представити у наступному вигляді: = a0 + a1 ´ y (3.20)
де sso - загальна собівартість продукції Т-150К за період, у - обсяг виробництва,0 та a1 - параметри моделі.
Рисунок 3.2 - Залежність загальної собівартості від обсягу виробництва
Використовуючи пакет Статистика було розраховано параметри моедлі та перевірена їх статистична значущість (табл. 3.4). Розрахувавши по кількості спостережень параметри а0 і а1, одержали таку залежність загальної собівартості від обсягу виробництва:
sso = 448026,9+81374,8 ´ y
Таблиця 3.4 - Розрахунок параметрів моделі
Розрахований коефіцієнт детермінації для даної моделі має значення рівне 0,998, тобто побудовану модель можна використовувати для прогнозу. Проведемо аналіз параметрів моделі У даній моделі параметр а0 - const, він відображає постійні витрати в загальній собівартості продукції, що не залежать від обсягу виготовленої продукції; а1 - змінні витрати на одиницю виробу, що знаходяться в прямій залежності від у. В даному випадку, якщо обсяг виробництва у дорівнює 0, то підприємство завжди несе витрати, що дорівнюють постійним, тобто sso = а0. Аналіз за допомогою 2-х даних економетричних моделей дозволяє зробити висновок, що в розглянутих залежностях присутній "ефект масштабу", тобто при зростанні обсягу виробництва собівартість одиниці виробу зменшується, а загальна собівартість відповідно росте, і навпаки, при зменшенні обсягу виробництва собівартість одиниці продукції збільшується, а загальна - знижується.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-27; просмотров: 69; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.43.204 (0.007 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


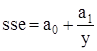 (3.18)
(3.18)
 (3.19)
(3.19) - постійні витрати на одиницю обсягу виробництва. Слід зазначити, що загальні змінні витрати при збільшенні обсягу виробництва збільшуються, однак змінні витрати на одиницю обсягу виробництва залишаються незмінними, тобто змінними витратами на виробництво одиниці продукції в побудованій моделі є коефіцієнт а0. Це висловлювання можна підтвердити якщо знайти ліміт співвідношення
- постійні витрати на одиницю обсягу виробництва. Слід зазначити, що загальні змінні витрати при збільшенні обсягу виробництва збільшуються, однак змінні витрати на одиницю обсягу виробництва залишаються незмінними, тобто змінними витратами на виробництво одиниці продукції в побудованій моделі є коефіцієнт а0. Це висловлювання можна підтвердити якщо знайти ліміт співвідношення 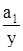 , якщо у ® ¥. Це співвідношення буде прагнути до 0, тобто собівартість одиниці продукції при достатньо великих обсягах виробництва буде прагнути до змінних витрат виробництва.
, якщо у ® ¥. Це співвідношення буде прагнути до 0, тобто собівартість одиниці продукції при достатньо великих обсягах виробництва буде прагнути до змінних витрат виробництва.



