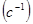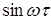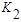Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение области устойчивости системы.Содержание книги Поиск на нашем сайте
1. Характеристический полином замкнутой системы получим из выражения:
Отсюда: Д(р) = 2. Уравнение апериодической границы устойчивости соответствует при Р=0. Получаем:
Найдем колебательную границу устойчивости, для этого подставим: Р= j w
Тогда:
Решив уравнение относительно К1 и К2 , найдем выражение для колебательной границы устойчивости в виде:
Рассчитываем три точки колебательной границы устойчивости при w=0; Dw; 2Dw.
СТУДЕНТ Ситников С.А. ГРУППА 2102
РАСЧЕТ ОБЛАСТИ УСТОЙЧИВОСТИ (ЛИНИИ РАВНОГО ЗАПАСА УСТ.) НЕПРЕР.АСР ПАРАМЕТРЫ МОДЕЛЕЙ ИЗВЕСТНОЙ ЧАСТИ СИСТЕМЫ
МОДЕЛЬ ОБЪЕКТА ПО КАНАЛУ УПРАВЛЕНИЯ: коэффициент передачи объекта = 112.0000 постоянная времени объекта = 50.0000 запаздывание объекта = 120.0000
Коэф.передачи исполн.устройства = 1.0000 Коэф.передачи регулир.органа = 0.0104 Коэффициент передачи датчика = 0.2500
РАСЧЕТ ОБЛАСТИ УСТОЙЧИВОСТИ
АПЕРИОДИЧЕСКАЯ ГРАНИЦА УСТОЙЧИВОСТИ K2 = 0
ТАБЛИЦА КОЛЕБАТЕЛЬНОЙ ГРАНИЦЫ УСТОЙЧИВОСТИ W K1 K2 0.000000 -3.434066 0.000000 0.001538 -3.327219 0.001369 0.003077 -3.011959 0.005329 0.004615 -2.503887 0.011447 0.006154 -1.828233 0.019034 0.007692 -1.018726 0.027196 0.009231 -0.116080 0.034896 0.010769 0.833836 0.041032 0.012308 1.782074 0.044517 0.013846 2.678837 0.044370 0.015385 3.475768 0.039792 0.016923 4.128202 0.030245 0.018462 4.597282 0.015513 0.020000 4.851844 -0.004253
РАСЧЕТ ЛИНИИ РАВНОГО ЗАПАСА УСТОЙЧИВОСТИ
СТЕПЕНЬ КОЛЕБАТЕЛЬНОСТИ = 0.22
W K1 K2 0.000000 -3.434066 0.000000 0.001538 -2.954172 0.001362 0.003077 -2.334213 0.005027 0.004615 -1.620191 0.010232 0.006154 -0.858793 0.016105 0.007692 -0.095154 0.021747 0.009231 0.629134 0.026307 0.010769 1.277682 0.029049 0.012308 1.820598 0.029409 0.013846 2.235384 0.027029 0.015385 2.507436 0.021783 0.016923 2.630145 0.013783 0.018462 2.604631 0.003363 0.020000 2.439161 -0.008941
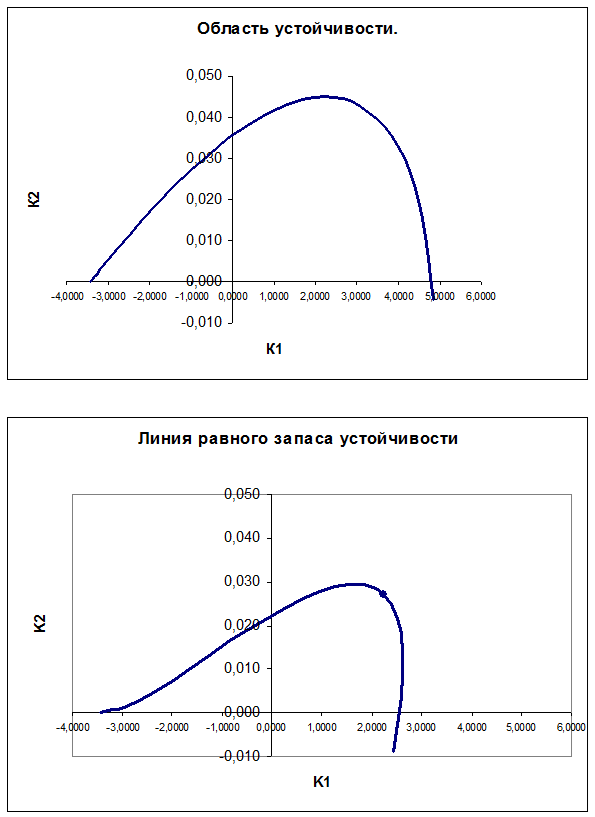
Область устойчивости системы в плоскости варьируемых параметров.
Определение направления штриховки колебательной границы устойчивости производится в соответствии со знаком определителя вида.
D(w)=
При перемещении вдоль колебательной границы в направлении возрастании частоты от 0 до ¥ кривая штрихуется слева, т. к. Dw > 0. Если частоту менять в пределах от - ¥ до 0 (w < 0), то определитель меняет знак и, двигаясь вдоль увеличения частоты, нужно штриховать правую часть кривой. Таким образом, кривая колебательной границы проходится дважды, при этом штрихуется одна и та же часть кривой двойной штриховкой. Апериодическая граница устойчивости штрихуется в сторону колебательной границы устойчивости.
Параметры регулятора K1; K2, выбранные из области устойчивости системы, обеспечат затухание переходной составляющей её движения при любых начальных отклонениях и внешних воздействиях.
Расчет линии равного запаса устойчивости. 1.Выведем выражение расширенной АФЧХ регулирующего блока Wр.б.(m1jw)
Передаточная функция:
Заменим р на (j - m)w:
Запишем
Тогда:
2.Выведем выражение расширенной АФЧХ части системы, содержащей остальные элементы в контуре управления.
Заменим р на
Запишем
Тогда:
Между заданной степенью колебательности m системы и характером расширенных и частотных характеристик с тем же m существует определенная связь. Для нахождения системы на границе заданной степени колебательности m, определяющей заданный запас устойчивости, необходимо выполнение следующего соотношения:
или в показательной форме
или
Получили два условия. Первое условие приводит к уравнению:
Второе условие к уравнению вида:
Решив уравнение относительно К1 и К2 получим:
Все значения К1 и К2, лежащие на кривой обеспечат заданные запас устойчивости. Значения К1 и К2, лежащие внутри области, ограниченной данной кривой и осями координат, обеспечат запас больше заданного или степень затухания больше заданной, а лежащие вне этой области – степень затухания меньше заданной. Специальными исследованиями было установлено, что настройки, расположенные чуть правее экстремума линии равного запаса устойчивости, обеспечивают минимум квадратичного интегрального критерия качества, поэтому эти настройки можно назвать оптимальными.
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-26; просмотров: 195; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.137.40 (0.01 с.) |

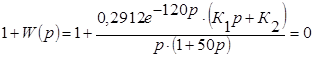


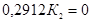 Þ К2 = 0
Þ К2 = 0 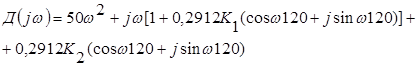

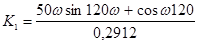


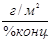

 =
= 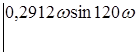
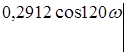 =
=
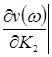

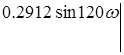
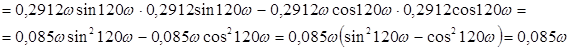
 ,
,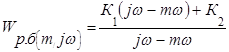
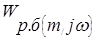 в виде
в виде =
=  , где
, где - расширенная АЧХ звена
- расширенная АЧХ звена -расширенная ФЧХ звена
-расширенная ФЧХ звена

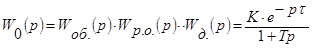 ,
,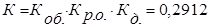


 , отсюда
, отсюда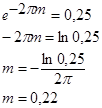
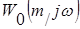 в виде
в виде