
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
V этап. Вывод уравнений для оценки показателей безотказности объекта.Содержание книги
Поиск на нашем сайте
Для оценки безотказности нагруженной детали на любой момент времени
V I этап. Формулирование уравнения перехода объекта в предельное состояние (состояние параметрического отказа). Уравнение перехода нагруженной детали в предельное состояние (состояние параметрического отказа по выбранному параметру
VI I этап. Вывод уравнений для оценки показателей долговечности (ресурса) объекта. Ресурс (длительность существования нагруженной детали до разрушения (отказа)) определяется решением уравнения (2.5) относительно
Предложенная методика (2.1) - (2.6) позволяет определять показатели безотказности (запас надежности Для упрощения расчетов по модели (2.1) - (2.6) при оценке долговечности нагруженных элементов механических систем в работе [1] предложена графическая интерпретация процесса определения ресурса
Рис. 2.2. Номограмма для оценки долговечности нагруженных элементов На данной номограмме для нагруженного элемента из стали 25 с указанными механическими свойствами, для расчетных значений напряжения Справочный материал для расчета показателей безотказности и долговечности нагруженных деталей машин и конструкций из различных материалов по методике (2.1) - (2.6), примеры расчетов, а также соответствующие типовые номограммы, представлены в приложении. В каждой последующей расчетно-практической работе используются оба способа оценки надежности нагруженных объектов: статический и кинетический. В качестве нагруженной детали рассматривается консольный стержень (балка), подвергаемый определенному виду нагружения внешними силовыми факторами: силой 2.2. Литература 1. Анцупов В.П., Анцупов А.В. (мл.), Анцупов А.В., Слободянский М.Г. Прогнозирование надежности деталей и узлов металлургического оборудования при их проектировании и эксплуатации: учеб. пособие. - Магнитогорск: Изд-во Магнитогорск. гос. тех. ун-та, 2012.-77 с. 2. Анцупов В.П., Корчунов А. Г. Анцупов А.В. (мл.), Анцупов А.В. Основы диагностики и надежности технических объектов: учеб. пособие. - Магнитогорск: Изд-во Магнитогорск. гос. тех. ун-та, 2012.-114 с. РАСЧЕТНО-ПРАКТИЧЕСКАЯ РАБОТА №3 «ОЦЕНКА НАДЕЖНОСТИ НАГРУЖЕННОГО ЭЛЕМЕНТА, ПОДВЕРЖЕННОГО РАСТЯЖЕНИЮ»
3.1. Цель работы Определить показатели надежности стержня, подверженного стационарному растяжению, по критериям статической и кинетической прочности и предложить способы повышения его долговечности.
3.2. Расчетная схема нагружения объекта Исследуемым объектом в данной работе является металлический стержень с пределом текучести материала
а б Рис.3.1. Расчетная схема а – схема внешнего нагружения элемента; б – эпюра нормальных напряжений в произвольном поперечном сечении стержня На схеме, рис.3.1:
3.3. Методика и контрольный пример расчета показателей надежности элемента по статическому критерию прочности
Методику расчета показателей безотказности и долговечности нагруженного стержня построим в соответствии с методологией (1.1)-(1.7). В качестве исходных данных для контрольного примера примем следующие значения необходимых для расчета параметров:
1. На первом этапе в качестве параметра состояния нагруженного стержня принимаем внутреннее напряжение - В соответствии со статическим подходом «Сопротивления материалов», растягивающее напряжение, возникающее в точках любого поперечного сечения нагруженного стержня от действия силы
где 2. На втором этапе формулируем уравнение (1.2) состояний объекта. Уравнение состояний нагруженного объекта представляет собой зависимость, определяющую изменение выбранного параметра (здесь Поскольку параметр состояния по условию (3.1) не зависит от времени
т.е. нагруженный элемент по выбранному параметру 3. На третьем этапе формулируем кинетическое уравнение (1.3) повреждаемости стержня в виде зависимости для оценки скорости изменения параметра состояния во времени - Учитывая (3.2), кинетическое уравнение (1.3) повреждаемости объекта вырождается в условие:
4. На четвертом этапе формулируем условие (1.4) работоспособности элемента и оцениваем вид его состояния. Условие работоспособности растягиваемого стержня, с учетом (3.2), запишем в виде:
Поскольку условие работоспособности выполняется, нагруженный стержень находится в работоспособном состоянии. 5. На пятом этапе формулируем уравнение (1.5) для оценки безотказности нагруженного стержня. С этой целью запишем выражение (1.5) и рассчитаем коэффициент запаса надежности элемента по выбранному параметру
6. На шестом этапе необходимо сформулировать уравнение (1.6) перехода элемента в предельное состояние. Однако, согласно условию (3.2) параметр состояния элемента имеет постоянное значение - Поэтому уравнение (1.6) перехода элемента в предельное состояние сформулировать невозможно, т. е. для заданных условий нагружения в любой момент времени
7. На седьмом этапе сформулируем уравнение (1.7) для оценки долговечности нагруженного стержня. Поскольку по условию (3.2) параметр состояния элемента имеет постоянное значение -
Вывод. С позиций статического подхода к оценке надежности нагруженных объектов, исследуемый стержень по выбранному параметру 3.4. Методика и контрольный пример расчета показателей надежности элемента по кинетическому критерию прочности
Методику расчета показателей безотказности и долговечности нагруженного стержня по кинетическому критерию прочности построим в соответствии с методологическим подходом (2.1)-(2.6). Расчетная схема растягиваемого стержня представлена рис. 3.1. В качестве исходных данных для контрольного примера примем следующие значения необходимых для расчета параметров: 1 группа. Внешние и внутренние параметры нагруженного элемента:
2 группа. Физико-механические характеристики материала стержня – Сталь 25, в исходном состоянии:
3 группа. Теплофизические характеристики материала:
4 группа. Основные физические константы:
1. На первом этапе в качестве параметра состояния нагруженного стержня принимаем плотность потенциальной энергии дефектов структуры материала 2. На втором этапе формулируем уравнение (2.1) состояний нагруженного стержня в виде:
где
3. На третьем этапе формулируем кинетическое уравнение (2.2) повреждаемости структуры локальных объемов материала стержня и определяем скорость
где
так как
4. На четвертом этапе формулируем условие (2.3) работоспособности элемента и оцениваем вид его состояния для назначенного ресурса Условие работоспособности (2.3), с учетом (3.8) и (3.9), запишем в виде:
где
Для назначенного ресурса
Поскольку условие работоспособности (3.10) для назначенного ресурса
нагруженный стержень на данный момент времени 5. На пятом этапе формулируем уравнение (2.4) для оценки безотказности нагруженного стержня. С этой целью запишем уравнение (2.4) и рассчитаем коэффициент запаса надежности элемента по выбранному параметру
6. На шестом этапе сформулируем уравнение (2.5) перехода нагруженного стержня в предельное состояние с учетом (3.8) и (3.10.а) в виде:
7. На седьмом этапе формулируем уравнение (2.6) для оценки долговечности нагруженного стержня. С этой целью решим уравнение (3.12) относительно
Вывод. Проведенные с позиций кинетического подхода расчеты показателей надежности исследуемого стержня, подверженного стационарному растяжению, показали следующее: - состояние нагруженного элемента по выбранному параметру - основной показатель безотказности растянутого стержня – запас его надежности по выбранному параметру: при при для назначенного в исходных данных ресурса - - прогнозируемый предельный ресурс исследуемого элемента (предельная длительность пребывания стержня под нагрузкой от момента ее приложения до момента отказа (разрушения)) составляет -
3.5. Графическая интерпретация кинетического подхода к определению ресурса нагруженного элемента Для упрощения расчетов при оценке долговечности нагруженных элементов механических систем, можно использовать типовые номограммы. Номограммы представляют собой графическую интерпретацию модели (2.1)–(2.6) процесса формирования отказа нагруженных элементов, выполненных из различных материалов, и служат для приближенной оценки их ресурса. В частности, номограмма для элементов, изготовленных из стали25, представлена на рис.3.2.
Рис. 3.2. Номограмма для оценки ресурса нагруженных элементов Ресурс исследуемого стержня, подверженного растяжению согласно расчетной схеме, рис.3.1, и приведенным исходным данным, можно оценить по номограмме следующим образом. По рассчитанному значению напряжения
3.6. Исследование способов повышения долговечности объекта
Данный раздел предназначен для приобретения студентами творческих навыков проведения аналитических исследований в виде разработки новых решений, направленных на повышение долговечности исследуемого технического объекта. Используя методику расчета (3.8) –(3.13) и номограмму на рис.3.2, каждому студенту необходимо самостоятельно решить следующие задачи. 1. Выяснить влияние на долговечность растянутого стержня следующих параметров: - растягивающей силы - температуры стержня - твердости поверхности стержня - диаметра стержня - применения новых марок стали: Ст45 (отжиг); Ст45 (нормализация); Ст45(закалка); Ст40Х (отжиг), 20Х13, характеристики которых представлены в приложении; - построить графики зависимостей: 2. На основании полученных результатов предложить практические способы повышения долговечности исследуемого в данной работе нагруженного элемента. 3.7. Общие выводы по работе В данном разделе необходимо выделить наиболее целесообразный подход к оценке надежности растягиваемого стержня и перечислить наиболее эффективные способы повышения его долговечности. РАСЧЕТНО-ПРАКТИЧЕСКАЯ РАБОТА №4 «ОЦЕНКА НАДЕЖНОСТИ НАГРУЖЕННОГО ЭЛЕМЕНТА, ПОДВЕРЖЕННОГО ИЗГИБУ»
4.1. Цель работы Определить показатели надежности стержня, подверженного стационарному изгибу, по критериям статической и кинетической прочности и предложить способы повышения его долговечности.
4.2. Расчетная схема нагружения объекта
Исследуемым объектом в данной работе является металлический стержень (балка) с пределом текучести материала
а б Рис.4.1. Расчетная схема а – схема внешнего нагружения элемента; б – эпюра нормальных напряжений в опасном поперечном сечении стержня На схеме, рис.4.1:
4.3 Методика и контрольный пример расчета показателей надежности элемента по статическому критерию прочности
Методику расчета показателей безотказности и долговечности нагруженного стержня построим в соответствии с методологией (1.1)-(1.7). В качестве исходных данных для контрольного примера примем следующие значения необходимых для расчета параметров:
1. На первом этапе в качестве параметра состояния нагруженного стержня принимаем внутреннее напряжение - В соответствии со статическим подходом «Сопротивления материалов», максимальное растягивающее напряжение, возникающее в точках опасного поперечного сечения изгибаемого стержня, определяется известным выражением согласно (1.1):
где
2. На втором этапе формулируем уравнение (1.2) состояний объекта. Уравнение состояний нагруженного объекта представляет собой зависимость, определяющую изменение выбранного параметра (здесь Поскольку параметр состояния по условию (4.1) не зависит от времени
т.е. нагруженный элемент по выбранному параметру 3. На третьем этапе формулируем кинетическое уравнение (1.3) повреждаемости стержня в виде зависимости для оценки скорости изменения параметра состояния во времени - Учитывая (4.2), кинетическое уравнение (1.3) повреждаемости объекта вырождается в условие:
4. На четвертом этапе формулируем условие (1.4) работоспособности элемента и оцениваем вид его состояния. Условие работоспособности растягиваемого стержня, с учетом (4.2), запишем в виде:
Поскольку условие работоспособности выполняется, нагруженный стержень находится в работоспособном состоянии по выбранному параметру 5. На пятом этапе формулируем уравнение (1.5) для оценки безотказности нагруженного стержня. С этой целью запишем выражение (1.5) и рассчитаем коэффициент запаса надежности элемента по выбранному параметру
6. На шестом этапе необходимо сформулировать уравнение (1.6) перехода элемента в предельное состояние. Однако, согласно условию (4.2) параметр состояния элемента имеет постоянное значение - Поэтому уравнение (1.6) перехода элемента в предельное состояние сформулировать невозможно, т. е. для заданных условий нагружения в любой момент времени
7. На седьмом этапе сформулируем уравнение (1.7) для оценки долговечности нагруженного стержня. Поскольку по условию (4.2) параметр состояния элемента имеет постоянное значение -
Вывод. С позиций статического подхода к оценке надежности нагруженных объектов, исследуемый стержень по выбранному параметру 4.4. Методика и контрольный пример расчета показателей надежности элемента по кинетическому критерию прочности
Методику расчета показателей безотказности и долговечности нагруженного стержня по кинетическому критерию прочности построим в соответствии с методологическим подходом (2.1)-(2.6). Расчетная схема растягиваемого стержня представлена рис. 4.1. В качестве исходных данных для контрольного примера примем следующие значения необходимых для расчета параметров: 1 группа. Внешние и внутренние параметры нагруженного элемента:
2 группа. Физико-механические характеристики материала стержня – Сталь 25, в исходном состоянии:
3 группа. Теплофизические характеристики материала:
4 группа. Основные физические константы:
1. На первом этапе в качестве параметра состояния нагруженного стержня принимаем плотность потенциальной энергии дефектов структуры материала 2. На втором этапе формулируем уравнение (2.1) состояний нагруженного стержня в виде:
где
3. На третьем этапе формулируем кинетическое уравнение (2.2) повреждаемости структуры локальных объемов материала стержня и определяем скорость
где
|
||||
|
Последнее изменение этой страницы: 2020-03-26; просмотров: 181; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.224.116 (0.008 с.) |

 принимают коэффициент запаса его надежности по выбранному параметру
принимают коэффициент запаса его надежности по выбранному параметру  [1, 2]:
[1, 2]: . (2.4)
. (2.4) ) с учетом (2.1) записывают в виде:
) с учетом (2.1) записывают в виде: . (2.5)
. (2.5) :
: . (2.6)
. (2.6) по условию (2.3)) и долговечности (ресурс
по условию (2.3)) и долговечности (ресурс  по условию (2.5)) любой нагруженной детали для рассчитанных значений максимальных напряжений
по условию (2.5)) любой нагруженной детали для рассчитанных значений максимальных напряжений  , температуры
, температуры  и физико-механических характеристик материала.
и физико-механических характеристик материала.
 и температуры
и температуры  , в направлении, указанном стрелками, определен его ресурс, равный
, в направлении, указанном стрелками, определен его ресурс, равный  .
. или моментом
или моментом  .
. , подверженный стационарному растяжению, расчетная схема которого представлена на рис.3.1.
, подверженный стационарному растяжению, расчетная схема которого представлена на рис.3.1.

 - диаметр стержня;
- диаметр стержня; - длина стержня;
- длина стержня; - растягивающая сила;
- растягивающая сила; - внутренняя продольная сила, возникающая в любом поперечном сечении стержня, растягиваемого внешней силой
- внутренняя продольная сила, возникающая в любом поперечном сечении стержня, растягиваемого внешней силой  - диаметр стержня;
- диаметр стержня; - длина стержня;
- длина стержня; - предел текучести материала – сталь 25;
- предел текучести материала – сталь 25; - растягивающая сила;
- растягивающая сила; - площадь поперечного сечения стержня.
- площадь поперечного сечения стержня. , возникающее в точках растягиваемого силой
, возникающее в точках растягиваемого силой  элемента, рис.3.1.б.
элемента, рис.3.1.б. , (3.1)
, (3.1) - внутренняя продольная сила, возникающая в любом поперечном сечении стержня, равная внешней силе из условия равновесия отсеченной части, рис.3.1.б.
- внутренняя продольная сила, возникающая в любом поперечном сечении стержня, равная внешней силе из условия равновесия отсеченной части, рис.3.1.б. ) во времени [2].
) во времени [2]. , то уравнение состояний (1.2) нагруженного стержня вырождается в следующее условие:
, то уравнение состояний (1.2) нагруженного стержня вырождается в следующее условие: , (3.2)
, (3.2) .
. . (3.3)
. (3.3) . (3.4)
. (3.4) . (3.5)
. (3.5) , и не изменяется во времени.
, и не изменяется во времени. . (3.6)
. (3.6) , и не изменяется во времени, т.е. условие его работоспособности (3.4) сохраняется сколь угодно долго, то его ресурс, согласно уравнению (1.7.а), равен бесконечности:
, и не изменяется во времени, т.е. условие его работоспособности (3.4) сохраняется сколь угодно долго, то его ресурс, согласно уравнению (1.7.а), равен бесконечности: . (3.7)
. (3.7) , а, следовательно, его ресурс равен бесконечности-
, а, следовательно, его ресурс равен бесконечности-  .
. - растягивающая сила;
- растягивающая сила; - диаметр стержня;
- диаметр стержня; - площадь поперечного сечения стержня;
- площадь поперечного сечения стержня; - напряжение в точках растянутого стержня;
- напряжение в точках растянутого стержня; - назначенный ресурс;
- назначенный ресурс; - модуль упругости;
- модуль упругости; - модуль сдвига;
- модуль сдвига; - коэффициент Пуассона;
- коэффициент Пуассона; - твердость материала по Виккерсу;
- твердость материала по Виккерсу; – плотность материала;
– плотность материала; - рабочая температура материала стержня;
- рабочая температура материала стержня; - энтальпия плавления в жидком состоянии;
- энтальпия плавления в жидком состоянии; - удельная теплоемкость материала (при температуре
- удельная теплоемкость материала (при температуре 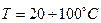 );
); - коэффициент линейного теплового расширения материала детали;
- коэффициент линейного теплового расширения материала детали; - энергия активации процесса разрушения межатомных связей при
- энергия активации процесса разрушения межатомных связей при  и
и  ;
; - коэффициент неравномерности распределения внутренней энергии по объему нагруженной детали (справочное значение);
- коэффициент неравномерности распределения внутренней энергии по объему нагруженной детали (справочное значение); - число Авогадро;
- число Авогадро; - постоянная Планка;
- постоянная Планка; - универсальная газовая постоянная;
- универсальная газовая постоянная; - постоянная Больцмана.
- постоянная Больцмана. , которая со скоростью
, которая со скоростью  возрастает со временем в поле приложенных внутренних постоянных напряжений -
возрастает со временем в поле приложенных внутренних постоянных напряжений -  .
. ; (3.8)
; (3.8) - начальное значение плотности скрытой энергии материала по (2.1.а):
- начальное значение плотности скрытой энергии материала по (2.1.а):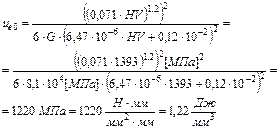 . (3.8.а)
. (3.8.а) , (3.9)
, (3.9) - коэффициент перенапряжения межатомных связей:
- коэффициент перенапряжения межатомных связей: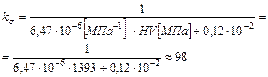 ; (3.9.а)
; (3.9.а) - коэффициент влияния шаровой части тензора напряжений на энергию активации разрушения межатомных связей:
- коэффициент влияния шаровой части тензора напряжений на энергию активации разрушения межатомных связей: ; (3.9.б)
; (3.9.б) - энергия активации процесса разрушения межатомных связей при данном напряжении
- энергия активации процесса разрушения межатомных связей при данном напряжении  и температуре
и температуре  :
: (3.9.г)
(3.9.г) - доля энергии активации, определяемая температурой:
- доля энергии активации, определяемая температурой: ; (3.9.д)
; (3.9.д) - коэффициент всестороннего сжатия материала при температуре
- коэффициент всестороннего сжатия материала при температуре  :
: ; (3.9.е)
; (3.9.е) - модуль упругости материала стержня при температуре
- модуль упругости материала стержня при температуре  ; (3.9.ж)
; (3.9.ж) -коэффициент Пуассона материала стержня при температуре
-коэффициент Пуассона материала стержня при температуре  ; (3.9.з)
; (3.9.з) - коэффициент эквивалентности квазистационарного напряженного состояния стационарному:
- коэффициент эквивалентности квазистационарного напряженного состояния стационарному: ; (3.9.и)
; (3.9.и) - коэффициент асимметрии цикла при статическом нагружении:
- коэффициент асимметрии цикла при статическом нагружении: ,
, .
. - модуль сдвига материала стержня при температуре
- модуль сдвига материала стержня при температуре  :
: . (3.9.к)
. (3.9.к) .
. ; (3.10)
; (3.10) - критическая плотность энергии дефектов структуры локальных объемов нагруженного стержня при температуре
- критическая плотность энергии дефектов структуры локальных объемов нагруженного стержня при температуре  ; (3.10.а)
; (3.10.а) - тепловая составляющая плотности внутренней энергии элемента твердого тела на момент разрушения согласно (2.3.в):
- тепловая составляющая плотности внутренней энергии элемента твердого тела на момент разрушения согласно (2.3.в): . (3.10.б)
. (3.10.б) плотность энергии дефектов структуры локальных объемов нагруженного стержня составит:
плотность энергии дефектов структуры локальных объемов нагруженного стержня составит: ; (3.10.г)
; (3.10.г) выполняется:
выполняется: , (3.10.д)
, (3.10.д) находится в работоспособном состоянии по выбранному параметру
находится в работоспособном состоянии по выбранному параметру  , который составит:
, который составит: . (3.11)
. (3.11) ; (3.12)
; (3.12) :
: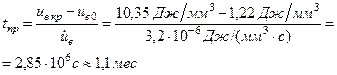 . (3.13)
. (3.13) , до критического, при котором
, до критического, при котором  ;
; , также зависит от длительности его пребывания под нагрузкой, т. е. изменяется (убывает) с течением времени:
, также зависит от длительности его пребывания под нагрузкой, т. е. изменяется (убывает) с течением времени: , запас -
, запас -  ;
; , запас -
, запас -  ;
; , запас надежности составляет -
, запас надежности составляет -  (см. (3.11));
(см. (3.11)); (см. (3.13)).
(см. (3.13)).
 , отложенному по оси абсцисс, и кривой, соответствующей заданному в исходных данных значению его рабочей температуры
, отложенному по оси абсцисс, и кривой, соответствующей заданному в исходных данных значению его рабочей температуры  , необходимо по оси ординат найти (считать) значение искомого ресурса. В данном случае он составит
, необходимо по оси ординат найти (считать) значение искомого ресурса. В данном случае он составит  , что приблизительно совпадает с его расчетным значением по условию (3.13).
, что приблизительно совпадает с его расчетным значением по условию (3.13). ;
; ;
;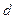 ;
; ;
;  ;
;  ;
;  , а также гистограмму по сравнительной оценке долговечности элементов, изготовленных из указанных марок стали.
, а также гистограмму по сравнительной оценке долговечности элементов, изготовленных из указанных марок стали. , подверженный стационарному изгибу, расчетная схема которого представлена на рис.4.1.
, подверженный стационарному изгибу, расчетная схема которого представлена на рис.4.1.

 - длина стержня;
- длина стержня; - внутренний максимальный изгибающий момент, возникающий в опасном поперечном сечении заделки стержня, изгибаемого внешней силой
- внутренний максимальный изгибающий момент, возникающий в опасном поперечном сечении заделки стержня, изгибаемого внешней силой  - максимальные внутренние напряжения, возникающие в наиболее нагруженных точках опасного поперечного сечения стержня в результате действия в нем внутреннего изгибающего момента
- максимальные внутренние напряжения, возникающие в наиболее нагруженных точках опасного поперечного сечения стержня в результате действия в нем внутреннего изгибающего момента  - диаметр стержня;
- диаметр стержня; - длина стержня;
- длина стержня; - предел текучести материала – сталь 25;
- предел текучести материала – сталь 25; - растягивающая сила.
- растягивающая сила. , возникающее в наиболее нагруженных точках опасного сечения элемента, изгибаемого силой
, возникающее в наиболее нагруженных точках опасного сечения элемента, изгибаемого силой  , рис.4.1.б.
, рис.4.1.б. , (4.1)
, (4.1) - внутренний изгибающий момент, действующий в опасном поперечном сечении стержня, равный моменту внешней силы
- внутренний изгибающий момент, действующий в опасном поперечном сечении стержня, равный моменту внешней силы  - осевой момент сопротивления опасного сечения стержня повороту при его изгибе силой
- осевой момент сопротивления опасного сечения стержня повороту при его изгибе силой 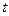 , то уравнение состояний (1.2) нагруженного стержня вырождается в следующее условие:
, то уравнение состояний (1.2) нагруженного стержня вырождается в следующее условие: , (4.2)
, (4.2) .
. . (4.3)
. (4.3) . (4.4)
. (4.4) . (4.5)
. (4.5) , и не изменяется во времени.
, и не изменяется во времени. . (4.6)
. (4.6) , а, следовательно, его ресурс равен бесконечности-
, а, следовательно, его ресурс равен бесконечности-  - длина стержня;
- длина стержня; - максимальные напряжения в наиболее нагруженных точках изогнутого стержня;
- максимальные напряжения в наиболее нагруженных точках изогнутого стержня; - назначенный ресурс;
- назначенный ресурс; - модуль упругости;
- модуль упругости; - модуль сдвига;
- модуль сдвига; - коэффициент Пуассона;
- коэффициент Пуассона; - твердость материала стержня по Виккерсу;
- твердость материала стержня по Виккерсу; - рабочая температура материала стержня;
- рабочая температура материала стержня; - энтальпия плавления в жидком состоянии;
- энтальпия плавления в жидком состоянии; - удельная теплоемкость материала (при температуре
- удельная теплоемкость материала (при температуре  );
); и
и  ;
; - коэффициент неравномерности распределения внутренней энергии по объему нагруженной детали (справочное значение);
- коэффициент неравномерности распределения внутренней энергии по объему нагруженной детали (справочное значение); - число Авогадро;
- число Авогадро; - постоянная Планка;
- постоянная Планка; - универсальная газовая постоянная;
- универсальная газовая постоянная; - постоянная Больцмана.
- постоянная Больцмана. , которая со скоростью
, которая со скоростью  возрастает со временем в поле приложенных внутренних постоянных напряжений -
возрастает со временем в поле приложенных внутренних постоянных напряжений -  ; (4.8)
; (4.8) - начальное значение плотности скрытой энергии материала по (2.1.а):
- начальное значение плотности скрытой энергии материала по (2.1.а): . (4.8.а)
. (4.8.а) , (4.9)
, (4.9) - коэффициент перенапряжения межатомных связей:
- коэффициент перенапряжения межатомных связей: ; (4.9.а)
; (4.9.а) - коэффициент влияния шаровой части тензора напряжений на энергию активации разрушения межатомных связей:
- коэффициент влияния шаровой части тензора напряжений на энергию активации разрушения межатомных связей: ; (4.9.б)
; (4.9.б) - энергия активации процесса разрушения межатомных связей при данном напряжении
- энергия активации процесса разрушения межатомных связей при данном напряжении  и температуре
и температуре  :
: (4.9.г)
(4.9.г) - доля энергии активации, определяемая температурой:
- доля энергии активации, определяемая температурой: ; (4.9.д)
; (4.9.д) - коэффициент всестороннего сжатия материала при температуре
- коэффициент всестороннего сжатия материала при температуре  :
: ; (4.9.е)
; (4.9.е) ; (4.9.ж)
; (4.9.ж)


