
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы сохранения в механикеСодержание книги Поиск на нашем сайте
ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ
Лабораторная работа №3. Динамика поступательного движения
Цель работы: углубить представление о механических силах, о работе и энергии; освоить методику и технику измерений; проверить на практике законы сохранения импульса и механической энергии; закрепить навыки обработки и представления экспериментальных наблюдений.
Оборудование: Линейка-желоб, линейка ученическая, две шайбы (шашки).
Задание 1. Определение коэффициента трения. Для определения коэффициент трения скольжения шайбы о поверхность линейки-желоба собирают установку в соответствии с рисунком, и подбирают такой угол наклона α, при котором шайба равномерно скользит по её поверхности. Коэффициент трения в этом случае равен тангенсу угла наклона k 1 = tg α. (1)
Таблица 1. Результаты измерения коэффициента трения по линейке-желобу.
k 1 =……… Работа силы трения на всей длине S 1 наклонной плоскости равна А= k 1 mgcos α∙ S = k 1 mg L. В соответствии с законом сохранения энергии, шайба, скатившаяся с высоты h, в конце наклонной плоскости обладает кинетической энергией mv2/2 = mgh – k 1 mgL (2) За счет этой энергии она продолжит движение по горизонтальной поверхности и остановится на таком расстоянии S 2 от основания наклонной плоскости, когда работа силы трения сравняется с исходным значением кинетической энергии. Отсюда получаем: mgh – k 1 mgL = k 2 mgS 2 (3) где k 2 - коэффициент трения скольжения шайбы по столу. Отсюда находим k 2 = (h - k 1 L)/ S 2 (4) В соответствии с описанной методикой проделайте измерения и определите коэффициенты трения скольжения шайбы о поверхности линейки-желоба и стола. Результаты занесите в таблицу 2. Оцените статистические погрешности измерений и представьте результаты в форме интервала.
Таблица 2. Результаты определения коэффициента трения по столу.
k 2=………±………… Задание 2. Определение мгновенной скорости шайбы. Скорость шайбы в конце скатывания можно определить экспериментально следующим способом. Установите наклонную плоскость возле края стола и так, чтобы шайба, пройдя после скатывания 2-3 см, начала свободно падать. Время ее падения можно определить по формуле t =√(2 h / g), где h - высота стола. Измерив расстояние l, которое она пролетает по горизонтали от края стола, вычисляют скорость ее горизонтального движения V=<l>/√(2h/g) (5)
Таблица 3. Результаты определения мгновенной скорости шайбы в конце наклонной плоскости.
V =………±………… Скорость шайбы в конце скатывания можно определить также из формулы (2): V2=2g(h – kL) (6)
Рассчитайте значение мгновенной скорости для той же высоты скатывания и сравните с экспериментальными результатами. Объясните полученный результат.
Таблица 4. Результаты расчета мгновенной скорости шайбы в конце наклонной плоскости.
Задание 3. Проверка закона сохранения энергии. По вычисленному в задании 2 значению скорости можно определить кинетическую энергию шайбы в момент выхода ее на стол. При дальнейшем движении сила трения о поверхность стола тормозит ее и останавливает на некотором расстоянии ST (тормозной путь). Для этого случая закон сохранения энергии принимает вид mV 2 /2= k 2 mgST (7) Воспользовавшись измеренным в задании 1 значением коэффициента трения k 2, рассчитайте тормозные пути для всех трех случаев, рассмотренных в задании 2. Затем определите эти же тормозные пути - S р - экспериментально. Результаты занесите в таблицу 5. Дайте объяснение полученным расхождениям теории и практики.
Таблица 5. Сравнение теоретических ST и реальных тормозных S р путей шайбы.
Задание 4. Проверка закона сохранения импульса. Опыт производится следующим образом. Вблизи основания наклонной плоскости устанавливается вторая шайба. На поверхности стола отмечают положение её центра. Шайба, падающая сверху наклонной плоскости, ударяется о неё упруго. Удар может быть прямым или косым, поэтому следует провести два экспериментальных наблюдения. 1. При прямом ударе первая шайба останавливается, а вторая продолжаетеё движение. По длине траектории определите её скорость и начальный импульс р2. Сравните полученный результат с импульсом р1 первой шайбы. Результаты сравнений занесите в отчет без таблицы, в свободной форме.
2. После «косого» столкновения движутся обе шайбы, их траектории образуют некоторый угол. В эксперименте следует отметить положение каждой из них в момент столкновения и конечные точки их разлета. Поскольку массы шайб одинаковы, а тормозные пути пропорциональны квадратам их скоростей (см. формулы 6 и 7), то значения импульсов пропорциональны корням квадратным из их тормозных путей: p 1 ~ m √ S 1 p 2 ~ m √ S 2 (8) С учетом векторного характера импульса проверку закона сохранения импульсов в этом случае нужно произвести путем построения четырехугольника на сторонах фигуры, получившейся после эксперимента. В идеальном случае должен получиться параллелограмм Воспользовавшись теоремой косинусов можно записать соотношение
Выполнение задания начинают с подбора высоты наклонной плоскости - длина тормозного пути S Т при этом должна быть достаточно большой, а разброс значений – минимальным. Затем отмечают положение первой шайбы на столе (обводят ее по контуру) в том месте, где она сходит с наклонной плоскости. Вторая шайба должна касаться этого контура. Точка касания задает вид удара - прямой или косой. Для точного воспроизведения серии ударов исходное положение второй шайбы также фиксируют при помощи контура. Контур наносится мягким карандашом, по завершении работы все линии со стола удаляют ластиком. После разлета шайб отмечают их положение, измеряют тормозные пути S 1 и S 2 - расстояния между центрами, и угол α между ними. Отчетом к этому заданию является лист формата А4, на который переносят точки и линии наиболее удачного опыта (см. рисунок). На этом же листе в масштабе строят четырехугольник векторов импульсов.
Лабораторная работа №4 Задание 1. Исследование затухания колебаний маятника
Упражнение 1. Закон затухания. Для получения количественных результатов проделайте следующие измерения. Отклоните маятник вправо на максимально возможный угол (диск не должен покидать поверхность пластины!), отметьте это положение и отпустите его. Отметьте фломастером каждое последующее амплитудное отклонение с этой же стороны до его полной остановки. Измерьте и занесите в таблицу длины дуг (А), соответствующих каждому отклонению. Произведите предписанные в таблице математические действия и сформулируйте «закон затухания гармонических колебаний».[3]
Таблица 1. Результаты исследования затухания колебаний.
……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………… Упражнение 2. Сила сопротивления. Определите длину пути, пройденного маятником до остановки S = 2(А1 + 2А2 + 2А3 + 2А4 + …….2Аn). Закон сохранения энергии дает в этом случае право записать соотношение mgh = <F>S (1) где m - масса маятника (указана на диске), h - высота его первоначального отклонения, < F > - средняя сила сопротивления. Найдите отсюда среднее значение силы сопротивления.
m = , g = , h = , S = , <F> = . Задание 2. Законы сохранения импульса и энергии Отклонив первый маятник на максимальный угол, отпустите его. К моменту прохождения точки равновесия он приобретает некоторую скорость - запас потенциальной энергии диска переходит в кинетическую энергию. Пренебрегая работой против сил сопротивления ввиду ее малости, из закона сохранения энергии mgh = mV 2 /2, можно вывести V =√2 gh (2) Рядом с первым подвесьте второй маятник точно таких же размеров и так, чтобы они в положении равновесия касались друг друга. Если теперь один из них отвести в сторону и отпустить, то в точке равновесия он будут обмениваться импульсами и энергиями. При столкновении тел в механике различают два крайних, идеализированных случая - упругий и неупругий удар. Абсолютно упругим считается такой удар, после которого тела движутся раздельно, а их суммарная механическая энергия не уменьшается. При неупругом ударе часть механической энергии тел переходит во внутреннюю и тела движутся совместно. Рассмотрим эти два случая раздельно. ОТЧЕТ ……………………………………………………………………………. о выполнении лабораторной работы №1 Задание 3. Проверка закона сохранения энергии.
Таблица 5. Сравнение теоретических ST, и реальных тормозных S р путей
Задание 4. Проверка закона сохранения импульса. ОТЧЕТ ……………………………………………………………………………. о выполнении лабораторной работы №2 Задание 1. Исследование затухания колебаний маятника
Упражнение 1. Закон затухания. Таблица 1. Результаты исследования затухания колебаний.
…Колебания затухают постепенно, причем так, что отношение амплитуды предыдущего колебания к амплитуде последующего можно считать постоянным. С учетом погрешности измерений оно в нашем опыте равно 1.31
Задание 2. Законы сохранения импульса и энергии Задание 3. Наблюдение связанных колебаний Упражнение 1. Маятники имеют одинаковые длины, сила связи задается одним грузом. Упражнение 2. Маятники имеют одинаковые длины, сила связи задается тремя грузами. Упражнение 3. Маятники имеют разные длины, сила связи задается одним грузом, начинает колебания длинный маятник. Упражнение 4. Маятники имеют разные длины, сила связи задается одним грузом, начинает колебания короткий маятник. ОТЧЕТ ---------------------------------------------------------------------------------------------- ОТЧЕТ ------------------------------------ ОТЧЕТ ------------------------------------ ОТЧЕТ ------------------------------------ ОТЧЕТ ------------------------------------ ОТЧЕТ ------------------------------------ ОТЧЕТ ------------------------------------ ОТЧЕТ ……………………………………………………………….. о выполнении лабораторной работы №3 «Кинематика вращательного движения» ……………октября 2005 года, СТИС, каф. ЕНД
Задание 1. Измерение угловой скорости вращения ω= φ/ t Оборудование: маятник Обербека, секундомер, метровая линейка, грузы.
Опустите нить с грузом так, чтобы он касался пола, и, медленно вращая маятник, поднимите груз на такую высоту, когда маятник сделает максимальное целое число оборотов N. Угол φ его поворота за это время составит 360∙ N градусов или 6,28∙ N радиан. Затем отпустите груз и измерьте время t его падения с этой высоты. Вычислите среднюю угловую скорость вращения маятника по формуле ω= φ/ t в радианах в секунду. h =…….. см N = …… об. φ=……..град; φ=…….рад. t1 =…….. t2 =…….. t3 =…….. t = ср …….. Δt ср =…….. δt =……%. ωср =……с-1; Δ ωср =……с-1; δ ω=……%. ω=ωср ± Δ ωс с-1; ω =………±……..с-1; δ ω=……%. Задание 2. Проверка закона углов поворота (В случае равноускоренного движения угол поворота увеличивается пропорционально квадрату времени). Оборудование прежнее Вращая маятник, отметьте такие положения (высоту) груза, которым соответствуют целые числа его оборотов – N 1, N 2, N 3, N 4, N 5 . Затем измерьте времена падения груза с каждой из этих высот. Полученные пары значений углов поворота и времени падения (они же времена вращения маятника) сопоставьте в виде отношений (φ i / ti 2) Таблица 1.
Вывод: Задание 3. Измерение углового ускорения ε = Δω/Δ t = 2φ/ t 2 Для определения углового ускорения воспользуемся данными, полученными во втором задании. Перенесите три первые строки в таблицу 2 и произведите вычисления.
Таблица 2.
ОТЧЕТ ------------------------------------ Статика. Цель работы: Углубить представление о видах и условиях равновесия твердого тела, имеющего ось вращения. Научить определять экспериментально и рассчитывать теоретически положение центра масс и центра тяжести тел. Проверить на опытах правило моментов.
Оборудование: Штатив, нить с грузом (отвес), плоские тела геометрически правильной и неправильной формы, отрезки проволоки диаметром до 3 мм и длиной до 40 см; линейка ученическая; набор шаров с отверстиями.
Задание 1. Определение положения центров тяжести плоских тел. 1.1. При помощи отвеса определите положение центра тяжести круга – плоского и однородного по материалу и толщине. Методика измерений показана на рисунке. Сравните с положением его геометрического центра.
1.2. Сектор.
1.3. Треугольник. Определите положение центра тяжести плоского однородного треугольника. Найдите те характеристики треугольника, которые позволяют найти ЦТ путем геометрических построений.
Отчеты по этому заданию представьте в натуральном виде: проставьте на телах положения центров тяжести (ЦТ) и укажите их расстояние от геометрического центра в долях радиуса.
Задание 2. Определение центров тяжести сложных тел
2.2. Проволока с шарами: Нанижите на стержень 2 – 3 шарика в произвольных положениях и зафиксируйте их там при помощи малого кусочка пластилина. Определите экспериментально положение ЦТ этого образца. Приняв один из концов проволоки за нуль оси ОХ, измерьте координату Х1 ЦТ. Измерьте координаты шариков и середины проволоки и рассчитайте теоретически положение ЦТ этого же образца. Масса шарика …… г, проволоки - …… г.
2.3. Изогнутая проволока. Изогните проволоку под прямым углом в точке, делящей ее в отношении 3:1. Определите положение ЦТ экспериментально. Для закрепления отвеса на проволоке и самой проволоки на оси вращения ее концам придана форма кольца. В качестве отчета по результатам измерений представьте рисунок с соблюдением пропорций.
2.4. Теоретический расчет. Для изогнутой проволоки произведите теоретический расчет положения ЦТ с использованием правила моментов. Сравните полученный результат с полученным в эксперименте. Проверьте результаты эксперимента и теоретических расчетов графическим методом. Результаты представьте в письменной форме.
Контрольные вопросы. 1. Что такое центр тяжести тела? Для чего его ввели в механику? 2. Назовите виды равновесия твердых тел в поле силы тяжести. 3. Что такое момент силы? Как он направлен? Какими единицами измеряется? 4. Запишите уравнения равновесия твёрдого тела. 5. Можно ли встать со стула, не наклоняясь вперед? Проверьте на собственном опыте. 6. Встав спиной вплотную к стене, попробуйте достать руками пятки своих ног и вновь выпрямиться. Почему сделать это не удается? 7. Что в ложке тяжелее, «держало» или «черпало»? 8. Сидеть – лучше, чем стоять; лежать – лучше, чем сидеть; ….. Почему? 9. Гоночным автомобилем «Формула 1» водитель управляет лежа. Почему? 10. Однородное по толщине бревно, как и доска, плавает «лежа». Почему не «стоя»? 11. Назовите два основных способа увеличения устойчивости тела, имеющего площадь опоры. Лабораторная работа №6 Момент инерции Цель работы: Углубить представление об инертности тел во вращательном движении, о моменте инерции, как количественной мере этого свойства тела. Проверить на опытах зависимость момента инерции от массы и характера ее распределения вдоль радиуса вращения.
Оборудование: Штатив; набор проволок диаметром 0.4 – 0.6 мм и длиной до 50 см; отрезки проволоки длиной 20-30 см; 3-4 шарика с отверстиями; линейка ученическая; секундомер;
Теоретическая часть
Рис.1. Моменты инерции некоторых тел для указанных осей вращения. Диск (цилиндр) J = mr 2 /2. Стержень J = ml 2 /12. Пластина размером а xbJ = m (a + b)2/12. Обруч J=mr2. Диск J=mr2/4 Если закрепить тело на упругом подвесе и, придав ему начальное угловое смещение, отпустить, то оно начнет совершать крутильные колебания вокруг подвеса, как оси вращения. Период таких колебаний зависит от момента инерции J и модуля упругости кручения D подвеса: T =2π√(J / D), (1) откуда J = T 2 D /4 π2. (2) Последней формулой можно пользоваться для сравнения моментов инерции разных тел. Чтобы получить численные значения моментов инерции произвольных тел необходимо предварительно вычислить момент инерции используемой в работе прямой шинки. Для этого воспользуемся формулой J 0 = ml 2 /12, и известными массой (m = г) и длиной (l = см). В последующем опыт проводят с одним и тем же подвесом (D=const), поэтому можно пользоваться соотношением J=Jo(T/To)2, (3) где Jo= г∙см2.
Экспериментальная часть Задание 1. Зависимость момента инерции от массы тела.
Прикрепите (скотчем) к первой вторую медную шинку такой же длины и вновь определите период колебаний Т2. По формуле (3) вычислите момент инерции J 2. Найдите отношение моментов J 2 / J о сравните с отношением масс m 2 / mo =2. Сделайте вывод о виде зависимости момента инерции тела от его массы.
Изогнув шинку так, как показано на рисунке, измените распределение массы вдоль ее радиуса вращения. Определите период колебаний такой шинки и, сравнив его с периодом колебаний прямой шинки, сделайте вывод о том, как зависит момент инерции тела от распределения его массы. Примечание: В первом случае расстояние от оси вращения до центров тяжести левой и правой половин шинки равно ј ее длины; во втором – зависит от угла изгиба. Рассчитайте эти расстояния самостоятельно для углов 60 и 30 градусов и свяжите эти размеры с моментами инерции.
Задание 3. Зависимость момента инерции тела от положения в нем оси вращения.
Задание 4-а. Адитивность момента инерции.
Задание 4-б. Закрепляя на прямой шинке шарики одинаковой массы симметрично относительно ее центра тяжести, проверьте, выполняется ли закон сложения моментов импульса системы тел.
Задание 5. Момент импульса вращательного движения. Опыты с гироскопом и на скамье Жуковского. (Проводятся в форме демонстраций с пояснениями)
Контрольные вопросы 1. Что является мерой инертности в поступательном движении? В колебательном? Во вращательном? 2. Как рассчитывается момент инерции материальной точки? 3. Как записывается второй закон динамики для вращательного движения? 4. Что такое момент силы? Как он направлен? 5. Какие величины используют для описания вращательного движения? 6. Что такое период колебаний? Каковы единицы его измерения? 7. Как момент инерции зависит от массы тела? 8. Как распределение массы тела вдоль радиуса вращения влияет на момент инерции? 9. Сколько моментов инерции у обруча? у стержня? у цилиндра? 10. Как спортсмен, прыгая с трамплина в воду, управляет скоростью своего вращения? 11. Что собой представляют гиродины космического корабля? Как они действуют? 12. От чего и как зависит кинетическая энергия вращающегося тела?
1.2. Примечание: Конец наклонной плоскости можно немного загнуть так, чтобы влет тела происходил горизонтально. Это облегчает дальнейшие расчеты. [3] Полученный ряд числовых значений укладывается в простую закономерность: А1/А2 = А2/А3 = А3/А4 = ….. = λ, где λ – декремент затухания.
ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ
Лабораторная работа №3.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-14; просмотров: 145; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.192.64 (0.013 с.) |

 (Можно воспользоваться соотношением tg α= h / L)
(Можно воспользоваться соотношением tg α= h / L) S21 +S22 +2S1S2cosα= S2 Т (8)
S21 +S22 +2S1S2cosα= S2 Т (8)







 По результатам опытов делают вывод о выполнимости закона сохранения импульса и причинах, влияющих на точность экспериментов.
По результатам опытов делают вывод о выполнимости закона сохранения импульса и причинах, влияющих на точность экспериментов.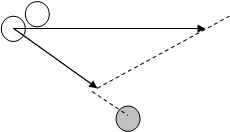
 Соберите экспериментальную установку – нитяной маятник - в соответствии с рисунком и так. Панель закреплена с небольшим отклонением от вертикали, поэтому диск своей плоскостью скользит по ее поверхности. Отведите диск от положения равновесия и отпустите его – маятник начнет совершать колебания. Вследствие действия трения скольжения и аэродинамического сопротивления колебания маятника через некоторое время прекращаются. Очевидно, что полученный им вначале запас потенциальной энергии расходуется на работу против сил сопротивления. Пронаблюдайте за тем, как затухают колебания маятника.
Соберите экспериментальную установку – нитяной маятник - в соответствии с рисунком и так. Панель закреплена с небольшим отклонением от вертикали, поэтому диск своей плоскостью скользит по ее поверхности. Отведите диск от положения равновесия и отпустите его – маятник начнет совершать колебания. Вследствие действия трения скольжения и аэродинамического сопротивления колебания маятника через некоторое время прекращаются. Очевидно, что полученный им вначале запас потенциальной энергии расходуется на работу против сил сопротивления. Пронаблюдайте за тем, как затухают колебания маятника.  Плоский однородный круг.
Плоский однородный круг. Вырежьте из круга сектор с центральным углом от 90 до 120о и определите положение центров тяжести этого сектора и оставшейся части круга.
Вырежьте из круга сектор с центральным углом от 90 до 120о и определите положение центров тяжести этого сектора и оставшейся части круга. 2.1. Проволока. Определите экспериментально положение ЦТ отрезка прямой проволоки. Сравните с положением ее геометрического центра. Запишите результаты в свободной форме.
2.1. Проволока. Определите экспериментально положение ЦТ отрезка прямой проволоки. Сравните с положением ее геометрического центра. Запишите результаты в свободной форме.
 Для материальной точки массой m, вращающейся по окружности радиусом r момент инерции определяется по формуле J = mr 2. Для протяженных тел правильной формы его величину вычисляют с применением теоремы Гюйгенса-Штейнера или методов дифференцирования и интегрирования.
Для материальной точки массой m, вращающейся по окружности радиусом r момент инерции определяется по формуле J = mr 2. Для протяженных тел правильной формы его величину вычисляют с применением теоремы Гюйгенса-Штейнера или методов дифференцирования и интегрирования. Подвес – медная проволока диаметром 0.4 мм и длиной 30-40 см. Исследуемое тело - медная шинка длиной 30 см. Закрепите подвес как можно ближе к центру тяжести шинки. Запустите крутильный маятник, определите время t полных десяти колебаний и вычислите период T о = t /10.
Подвес – медная проволока диаметром 0.4 мм и длиной 30-40 см. Исследуемое тело - медная шинка длиной 30 см. Закрепите подвес как можно ближе к центру тяжести шинки. Запустите крутильный маятник, определите время t полных десяти колебаний и вычислите период T о = t /10.  Задание 2. Зависимость момента инерции тела от распределения его массы.
Задание 2. Зависимость момента инерции тела от распределения его массы. Объект исследования - металлическое кольцо. Вначале закрепите его так, чтобы ось вращения совпадала с осью кольца (см. рис.) и определите период колебаний. Затем измените точку крепления так, чтобы ось вращения лежала в плоскости кольца, и вновь определите период колебаний. Сравните полученные значения и сформулируйте ответ на вопрос, поставленный в задании.
Объект исследования - металлическое кольцо. Вначале закрепите его так, чтобы ось вращения совпадала с осью кольца (см. рис.) и определите период колебаний. Затем измените точку крепления так, чтобы ось вращения лежала в плоскости кольца, и вновь определите период колебаний. Сравните полученные значения и сформулируйте ответ на вопрос, поставленный в задании. Соберите (при помощи скотча) составное тело из кольца и прямой шинки. Определите период колебаний и, сравнив с периодом колебаний прямой шинки, определите момент инерции составного тела. Сравните полученный результат с моментами инерции шинки и кольца. Сделайте вывод из полученных результатов.
Соберите (при помощи скотча) составное тело из кольца и прямой шинки. Определите период колебаний и, сравнив с периодом колебаний прямой шинки, определите момент инерции составного тела. Сравните полученный результат с моментами инерции шинки и кольца. Сделайте вывод из полученных результатов.


