Реализация класса InorderIterator.

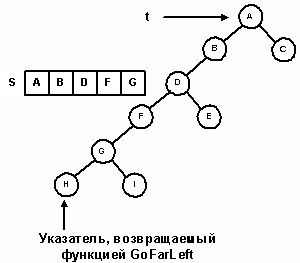
Итерационный симметричный метод прохождения эмулирует рекурсивное сканирование с помощью стека адресов узлов. Начиная с корня, осуществляется спуск вдоль левых поддеревьев. По пути указатель каждого пройденного узла запоминается в стеке. Процесс останавливается на узле с нулевым левым указателем, который становится первым посещаемым узлом в симметричном сканировании. Спуск от узла t и запоминание адресов узлов в стеке выполняет метод GoFarLeft. Вызовом этого метода с t=root ищется первый посещаемый узел (рис. 18).

 

// вернуть адрес крайнего узла на левой ветви узла t

// запомнить в стеке адреса всех пройденных узлов

 

template <class T>

 

TreeNode<T> *InorderIterator<T>::GoFArLeft(TreeNode<T> *t)

{

 // если t=NULL, вернуть NULL

 if (t == NULL)

 return NULL;

 

 // пока не встретится узел с нулевым левым указателем, спускаться по левым ветвям, запоминая в стеке S адреса пройденных узлов. Возвратить указатель на этот узел

 while (t->Left()!= NULL)

 {

 S.Push(t);

 t = t->Left();

 }

 return t;

}

 

Рис. 18.

 

После инициализации базового класса конструктор присваивает элементу данных root адрес корня бинарного дерева поиска. Узел для начала симметричного сканирования получается в результате вызова функции GoFarLeft с root в качестве параметра. Это значение запоминается в переменной сurrent.

 

// инициализировать флаг iterationComplete. Базовый класс сбрасывает его, но

// дерево может быть пустым. начальный узлел сканирования - крайний слева узел.

 

template <class T>

 

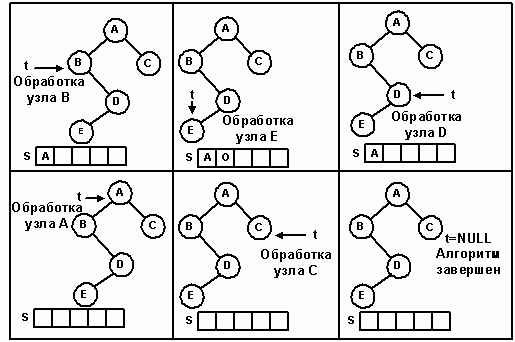
InorderIterator<T>::InorderIterator(TreeNode<T> *tree):

 Iterator<T>(), root(tree)

{

 iterationComplete = (root == NULL);

 current = GoFarLeft(root);

}

Метод Reset по существу является таким же, как и конструктор, за исключением того, что он очищает стек. Перед первым обращением к Next указатель current уже указывает на первый узел симметричного сканирования. Метод Next работает по следующему алгоритму. Если правая ветвь узла не пуста, перейти к его правому сыну и осуществить спуск по левым ветвям до узла с нулевым левым указателем, попутно запоминая в стеке адреса пройденных узлов.

Если правая ветвь узла пуста, то сканирование его левой ветви, самого узла и его правой ветви завершено. Адрес следующего узла, подлежащего обработке, находится в стеке. Если стек не пуст, удалить следующий узел. Если же стек пуст, то все узлы обработаны и сканирование завершено. Итерационное прохождение дерева, состоящего из пяти узлов, изображено на рисунке 19.

 

Рис. 19.

 

template <class T>

void InorderIterator<T>::Next(void)

{

 // ошибка, если все узлы уже посещались

 if (iterationComplete)

 {

 cerr << "Next: итератор прошел конец списка!" << endl;

 exit(1);

 }

 

 // current - текущий обрабатываемый узел

 // если есть правое поддерево, спуститься до конца по его левой ветви, попутно запоминая в стеке адреса пройденных узлов

 if (current->Right()!= NULL)

 current = GoFarLeft(current->Right());

 

 // правого поддерева нет, но в стеке есть другие узлы, подлежащие обработке.

 // Вытолкнуть из стека новый текущий адрес, продвинуться вверх по дереву

 else if (!S.StackEmpty())

 current = S.Pop();

 

 // нет ни правого поддерева, ни узлов в стеке. Сканирование завершено

 else

 iterationComplete = 1;

}

 

Алгоритм TreeSort.

Когда объект типа InorderIterator осуществляет прохождение дерева поиска, узлы проходятся в сортированном порядке и, следовательно, можно построить еще один алгоритм сортировки, называемый TreeSort. Этот алгоритм предполагает, что элементы изначально хранятся в массиве. Поисковое дерево служит фильтром, куда элементы массива копируются в соответствии с алгоритмом вставки в бинарное дерево поиска. Осуществляя симметричное прохождение этого дерева и записывая элементы снова в массив, мы получаем в результате отсортированный список. На рисунке 20 показана сортировка 8 - элементного массива.

 

#include "bstree.h"

#include "treeiter.h"

 

// использование бинарного дерева поиска для сортировки массива

template <class T>

 

void TreeSort(T arr[], int n)

{

 // бинарное дерево поиска, в которое копируется массив

 BinSTree<T> sortTree;

 int i;

 

 // вставить каждый элемент массива в поисковое дерево

 for (i=0; i<n; i++)

 sortTree.Insert(arr[i]);

 

 // объявить итератор симметричного прохождения для sortTree

 InorderIterator<T> treeSortIter(sortTree.GetRoot());

 

 // выполнить симметричное прохождение дерева

 // скопировать каждый элемент снова в массив

 i = 0;

 while (!treeSortIter.EndOfList())

 {

 arr[i++] = treeSortIter.Data();

 treeSortIter.Next();

 }

}

 

Рис. 20.