На тему: «реализация авл – деревьев через классы объектно – ориентированного программирования»

КУРСОВАЯ РАБОТА

 

По дисциплине «Объектно – ориентированное программирование»

На тему: «Реализация АВЛ – деревьев через классы объектно – ориентированного программирования»

 

Выполнил: ст. гр. СП – 07 – 1з Воронько О.А.

Проверил: Попивщий В.И.

 

 

Запорожье, 2009г.

 

ПЛАН

Введение

1. Основные термины

2. Основные операции с АВЛ - деревьями

3. Алгоритм реализации АВЛ – деревьев через классы объектно – ориентированного программирования

Список литературы

 

ВВЕДЕНИЕ

Язык программирования С++ является одним из наиболее популярных средств объектно – ориентированного программирования, позволяющим разрабатывать программы, эффективные по объему кода и скорости выполнения. С++ включает большое число операций и типов данных, средства управления вычислительными процессами, механизмы модификации типов данных и методы их обработки и, как следствие, является мощным языком программирования. Он позволяет описывать процессы обработки информации, начиная с уровня отдельных разрядов, видов и адресов памяти, переходя на основе механизмов объектно – ориентированного программирования к близким конкретным предметным областям понятиям.

Первые программы для цифровых вычислительных машин редко превышали объем 1 кбайт. Объемы используемых программ и программных систем измеряются не только десятками килобайтов, но и сотнями мегабайтов. Вместе с тем удельная стоимость создания программ (нормированная объемом программы) до последнего времени менялась мало. Более того, с ростом объема программы удельная стоимость ее создания могла нелинейно возрастать. Поэтому не удивительно, что одним из основных факторов, определяющих развитие технологии программирования, является снижение стоимости проектирования и создания программных продуктов (ПП), или борьба со сложностью программирования.

Другими важнейшими факторами, влияющими на эволюцию методов проектирования и создания ПП, являются:

· изменение архитектур вычислительных средств (ВС) в интересах повышения производительности, надежности и коммуникативности;

· упрощение взаимодействия пользователей с ВС и интеллектуализация ВС.

Действие двух последних факторов, как правило, сопряжено с ростом сложности программного обеспечения ВС. Сложность представляет неотъемлемое свойство программирования и программ, которое проявляется во времени и стоимости создания программ, в объеме или длине текста программы, характеристиках ее логической структуры, задаваемой операторами передачи управления (ветвления, циклы, вызовы подпрограмм и др.).

Можно выделить 5 следующих источников сложности программирования:

1) решаемая задача;

2) язык программирования;

3) среда выполнения программы;

4) технологический процесс коллективной разработки и создания ПП;

5) стремление к универсальности и эффективности алгоритмов и типов данных.

От свойства сложности нельзя избавиться, но можно изменять характеристики его проявления путем управления или организации.

В программировании широко используется фундаментальный принцип управления сложными системами, который известен человеку с глубокой древности – devide et impera (разделяй и властвуй, лат.) и широко им применяется при разработке и проектировании любых сложных технических систем.

В настоящее время объектно – ориентированное программирование (ООП) является доминирующим стилем при создании больших программ.

 

ОСНОВНЫЕ ТЕРМИНЫ

Так исторически сложилось, что у этих деревьев есть два альтернативных названия: АВЛ - деревья и сбалансированные деревья. АВЛ произошло от фамилий изобретателей.

Идеально сбалансированным называется дерево, у которого для каждой вершины выполняется требование: число вершин в левом и правом поддеревьях различается не более, чем на 1. Однако идеальную сбалансированность довольно трудно поддерживать.

В некоторых случаях при добавлении/удалении может потребоваться значительная перестройка дерева, не гарантирующая логарифмической сложности. Поэтому Г.М. Адельсон - Вельский и Е.М. Ландис ввели менее строгое определение сбалансированности и доказали, что при таком определении можно написать программы добавления/удаления, имеющие логарифмическую сложность и сохраняющие дерево сбалансированным.

Дерево считается сбалансированным по АВЛ (в дальнейшем просто «сбалансированным»), если для каждой вершины выполняется требование: высота левого и правого поддеревьев различаются не более, чем на 1. Не всякое сбалансированное дерево идеально сбалансировано, но всякое идеально сбалансированное дерево сбалансировано.

Бинарные деревья поиска предназначены для быстрого доступа к данным. В идеале разумно сбалансированное дерево имеет высоту порядка O(log2n). Однако при некотором стечении обстоятельств дерево может оказаться вырожденным. Тогда высота его будет O(n), и доступ к данным существенно замедлится. Рассмотрим модифицированный класс деревьев, обладающих всеми преимуществами бинарных деревьев поиска и никогда не вырождающихся. Они называются сбалансированными или АВЛ - деревьями. Под сбалансированностью будем понимать то, что для каждого узла дерева высоты обоих его поддеревьев различаются не более чем на 1.

Строго говоря, этот критерий нужно называть АВЛ - сбалансированностью в отличие от идеальной сбалансированности, когда для каждого узла дерева количества узлов в левом и правом поддеревьях различаются не более чем на 1. Здесь мы всегда будем иметь в виду АВЛ - сбалансированность.

Новые методы вставки и удаления в классе АВЛ - деревьев гарантируют, что все узлы останутся сбалансированными по высоте. На рисунках 1 и 2 показаны эквивалентные представления массива АВЛ - деревом и бинарным деревом поиска. Рисунок 1 представляет простой пятиэлементный массив А (A[5] = {1,2,3,4,5}), отсортированный по возрастанию. Рисунок 2 представляет массив B (B[8] = {20, 30, 80, 40, 10, 60, 50, 70}).

Бинарное дерево поиска имеет высоту 5, в то время как высота АВЛ - дерева равна 2. В общем случае высота сбалансированного дерева не превышает O(log2n). Таким образом, АВЛ - дерево является мощной структурой хранения, обеспечивающей быстрый доступ к данным.

Для этого используем подход, при котором поисковое дерево строится отдельно от своих узлов. Сначала разрабатываем класс AVLTreeNode, а затем используем объекты этого типа для конструирования класса AVLTree. Предметом пристального внимания будут методы Insert и Delete.

Они требуют тщательного проектирования, поскольку должны гарантировать, что все узлы нового дерева останутся сбалансированными по высоте.

 

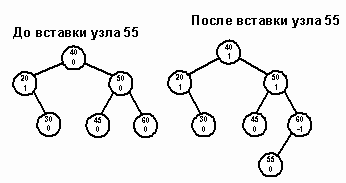
Класс AVLTree.

АВЛ - дерево представляет собой списковую структуру, похожую на бинарное дерево поиска, с одним дополнительным условием: дерево должно оставаться сбалансированным по высоте после каждой операции вставки или удаления. Поскольку АВЛ - дерево является расширенным бинарным деревом поиска, класс AVLTree строится на базе класса BinSTree и является его наследником.

Для выполнения АВЛ - условий следует изменить методы Insert и Delete. Кроме того, в производном классе определяются конструктор копирования и перегруженный оператор присвоения, так как мы строим дерево с большей узловой структурой.

Алгоритм АВЛ – вставки

Процесс вставки почти такой же, что и для бинарного дерева поиска. Осуществляется рекурсивный спуск по левым и правым сыновьям, пока не встретится пустое поддерево, а затем производится пробная вставка нового узла в этом месте. В течение этого процесса мы посещаем каждый узел на пути поиска от корневого к новому элементу. Поскольку процесс рекурсивный, обработка узлов ведется в обратном порядке. При этом показатель сбалансированности родительского узла можно скорректировать после изучения эффекта от добавления нового элемента в одно из поддеревьев. Необходимость корректировки определяется для каждого узла, входящего в поисковый маршрут. Есть три возможных ситуации. В двух первых случаях узел сохраняет сбалансированность и реорганизация поддеревьев не требуется. Нужно лишь скорректировать показатель сбалансированности данного узла. В третьем случае разбалансировка дерева требует одинарного или двойного поворотов узлов.

Случай 1. Узел на поисковом маршруте изначально является сбалансированным (balanceFactor = 0). После вставки в поддерево нового элемента узел стал перевешивать влево или вправо в зависимости от того, в какое поддерево была произведена вставка.

Если элемент вставлен в левое поддерево, показателю сбалансированности присваивается -1, а если в правое, то 1. Например, на пути 40 - 50 - 60 каждый узел сбалансирован. После вставки узла 55 показатели сбалансированности изменяются (рис. 6).

 

Рис. 6.

Случай 2. Одно из поддеревьев узла перевешивает, и новый узел вставляется в более легкое поддерево. Узел становится сбалансированным. Сравните, например, состояния дерева до и после вставки узла 55 (рис. 7).

Случай 3. Одно из поддеревьев узла перевешивает, и новый узел помещается в более тяжелое поддерево. Тем самым нарушается условие сбалансированности, так как balanceFactor выходит за пределы -1..1. Чтобы восстановить равновесие, нужно выполнить поворот.

 

Рис. 7.

Рассмотрим пример:

Предположим, что дерево разбалансировалось слева и мы восстанавливаем равновесие, вызывая одну из функций поворота вправо. Разбалансировка справа влечет за собой симметричные действия. Сказанное иллюстрируется рисунком 8.

Метод AVLInsert.

Продвигаясь вдоль некоторого пути для вставки нового узла, рекурсивный метод AVLInsert распознает все три указанных выше случая корректировки. При нарушении условия сбалансированности восстановление равновесия осуществляется с помощью функций UpdateLeftTree и UpdateRightTree.

 

template <class T>

 

void AVLTree<T>::AVLInsert(AVLTreeNode<T>* &tree,

 AVLTreeNode<T>* newNode, int &reviseBalanceFactor)

{

 // флаг "Показатель сбалансированности был изменен"

 int rebalanceCurrNode;

 

 // встретилось пустое поддерево, пора вставлять новый узел

 if (tree == NULL)

 {

 // вставить новый узел

 tree = newNode;

 

 // объявить новый узел сбалансированным

 tree->balanceFactor = balanced;

 

 // сообщить об изменении показателя сбалансированности

 reviseBalanceFactor = 1;

 }

 // рекурсивно спускаться по левому поддереву, если новый узел меньше текущего

 else if (newNode->data < tree->data)

 {

 AVLInsert(tree->Left(), newNode, rebalanceCurrNode);

 

 // проверить, нужно ли корректировать balanceFactor

 if (rebalanceCurrNode)

 {

 // вставка слева от узла, перевешивающего влево. будет нарушено

 // условие сбалансированности; выполнить поворот (случай 3)

 if (tree->balanceFactor == leftheavy)

 UpdateLeftTree(tree, reviseBalanceFactor);

 

 // вставка слева от сбалансированного узла.

 // узел станет перевешивать влево (случай 1)

 else if (tree->balanceFactor == balanced)

 {

 tree->balanceFactor = leftheavy;

 reviseBalanceFactor = 1;

 }

 

 // вставка слева от узла, перевешивающего вправо

 // узел станет сбалансированным (случай 2)

 else

 {

 tree->balanceFactor = balanced;

 reviseBalanceFactor = 0;

 }

 }

 Else

 

 // перебалансировка не требуется. не опрашивать предыдущие узлы

 reviseBalanceFactor = 0;

 }

// иначе рекурсивно спускаться по правому поддереву

 else if (newNode->data < tree->data)

 {

 AVLInsert(tree->Right(), newNode, rebalanceCurrNode);

 // проверить, нужно ли корректировать balanceFactor

 if (rebalanceCurrNode)

 {

 // вставка справа от узла, перевешивающего вправо. будет нарушено

 // условие сбалансированности; выполнить поворот (случай 3)

 if (tree->balanceFactor == rightheavy)

 UpdateRightTree(tree, reviseBalanceFactor);

 

 // вставка справа от сбалансированного узла

 // узел станет перевешивать вправо (случай 1)

 else if (tree->balanceFactor == balanced)

 {

 tree->balanceFactor = rightheavy;

 reviseBalanceFactor = 1;

 }

 // вставка справа от узла, перевешивающего влево

 // узел станет сбалансированным (случай 2)

 else

 {

 tree->balanceFactor = balanced;

 reviseBalanceFactor = 0;

 }

 }

 else

 // перебалансировка не требуется. не опрашивать предыдущие узлы

 reviseBalanceFactor = 0;

 }

 

Рис. 8.

 

Метод AVLInsert распознает случай 3, когда нарушается АВЛ - условие. Для выполнения перебалансировки используются методы UpdateLeftTree и UpdateRightTree. Они выполняют одинарный или двойной поворот для уравновешивания узла, а затем сбрасывают флаг reviseBalanceFactor. Перед тем, как обсудить специфические детали поворотов, приведем код функции UpdateLeftTree.

 

template <class T>

void AVLTree<T>::UpdateLeftTree(AVLTreeNode<T>* &p,

 int reviseBalanceFactor)

{

 AVLTreeNode<T> *lc;

 

 lc = p->Left();

 // перевешивает левое поддерево?

 if (lc->balanceFactor == leftheavy)

 {

 SingleRotateRight(p); // однократный поворот

 reviseBalanceFactor = 0;

 }

 // перевешивает правое поддерево?

 else if (lc->balanceFactor == rightheavy)

 {

 // выполнить двойной поворот

 DoubleRotateRight(p);

 // теперь корень уравновешен

 reviseBalanceFactor = 0;

}

 

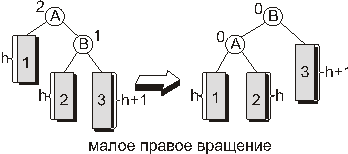
Малое правое вращение.

В случае, когда показатель сбалансированности вершины, в которой произошло нарушение баланса, равен 2, а показатель сбалансированности корня правого поддерева равен 1, восстановить сбалансированность в вершине можно с помощью преобразования, называемого малым правым вращением. Это вращение симметрично малому левому и схематично изображено на рисунке 10:

 

Рис. 10.

 

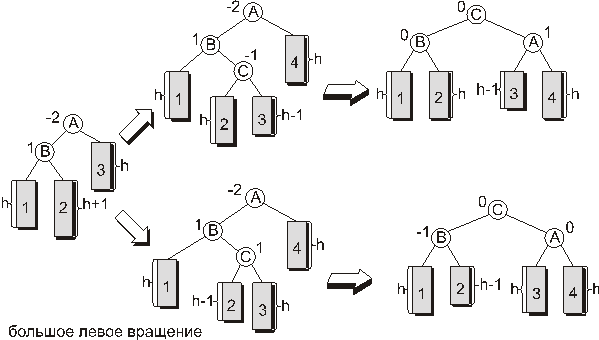
Большое левое вращение.

Несколько сложнее случай, когда показатель сбалансированности в вершине, в которой произошло нарушение баланса равен -2, а показатель сбалансированности в корне левого поддерева равен 1 или 0. В этом случае применяется преобразование, называемое большим левым вращением. Как видно из рисунка 11 здесь во вращении участвуют три вершины, а не две как в случае малых вращений.

 

Рис. 11.

 

Большое правое вращение.

Большое правое вращение применяется, когда показатель сбалансированности вершины, в которой произошло нарушение баланса, равен 2, а показатель сбалансированности корня правого поддерева равен -1 или 0. Большое правое вращение симметрично большому левому и схематично изображено на рисунке 12:

 

Рис. 12.

 

Повороты необходимы, когда родительский узел P становится разбалансированным. Одинарный поворот вправо (single right rotation) происходит тогда, когда родительский узел P и его левый сын LC начинают перевешивать влево после вставки узла в позицию X. В результате такого поворота LC замещает своего родителя, который становится правым сыном. Бывшее правое поддерево узла LC (ST) присоединяется к P в качестве левого поддерева. Это сохраняет упорядоченность, так как узлы в ST больше или равны узлу LC, но меньше узла P. Поворот уравновешивает как родителя, так и его левого сына (рис. 13).

 

// выполнить поворот по часовой стрелке вокруг узла p

// сделать lc новой точкой вращения

 

template <class T>

 

void AVLTree<T>::SingleRotateRight (AVLTreeNode<T>* &p)

{

 // левое, перевешивающее поддерево узла p

 AVLTreeNode<T> *lc;

 

 // назначить lc левым поддеревом

 lc = p->Left();

 

 // скорректировать показатель сбалансированности для родительского узла и его левого сына

 p->balanceFactor = balanced;

 lc->balanceFactor = balanced;

 

 // правое поддерево узла lc в любом случае должно оставаться справа от lc, выполнить это условие, сделав st левым поддеревом узла p

 p->Left() = lc->Right();

 // переместить p в правое поддерево узла lc

 // сделать lc новой точкой вращения

 lc->Right() = p;

 p = lc;

}

 

Рис. 13

 

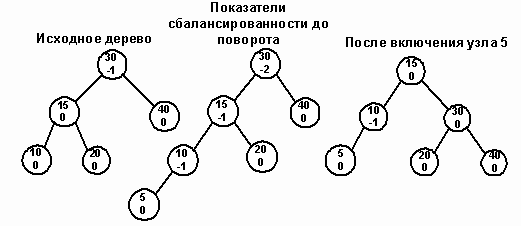
Рис. 14.

 

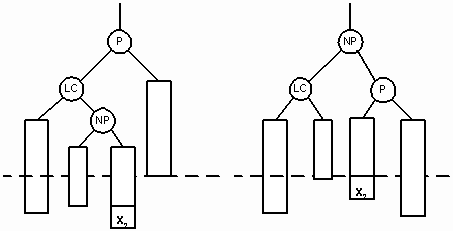
Попытка вставить узел 5 в изображенное на рисунке 14 АВЛ - дерево нарушает АВЛ - условие для узла 30. Одновременно левое поддерево узла 15 (LC) становится перегруженным.

Для переупорядочения узлов вызывается процедура SingleRotateRight. В результате родительский узел (30) становится сбалансированным, а узел 10 перевешивающим влево. Двойной поворот вправо (double right rotation) нужен тогда, когда родительский узел (P) становится перевешивающим влево, а его левый сын (LC) перевешивающим вправо. NP – корень правого перевешивающего поддерева узла LC. Тогда в результате поворота узел NP замещает родительский узел. На рисунках 15 и 16 показаны случаи вставки нового узла в качестве сына узла NP. В обоих случаях NP становится родительским узлом, а бывший родитель P становится правым сыном NP.

На рисунке 15 мы видим сдвиг узла X1, после того как он был вставлен в левое поддерево узла NP. На рисунке 16 изображено перемещение узла X2 после его вставки в правое поддерево NP.

 

Рис. 15.

 

Рис. 16

 

// двойной поворот вправо вокруг узла p

 

template <class T>

 

void AVLTree<T>::DoubleRotateRight (AVLTreeNode<T>* &p)

{

 // два поддерева, подлежащих повороту

 AVLTreeNode<T> *lc, *np;

 // узел lc <= узел np < узел p

 lc = p->Left(); // левый сын узла p

 np = lc->Right(); // правый сын узла lc

// обновить показатели сбалансированности в узлах p, lc и np

 if (np->balanceFactor == rightheavy)

 {

 p->balanceFactor = balanced;

 lc->balanceFactor = rightheavy;

 }

 else

 {

 p->balanceFactor = rightheavy;

 lc->balanceFactor = balanced;

 }

 np->balanceFactor = balanced;

 

 // перед тем как заменить родительский узел p, следует отсоединить его от старых детей и присоединить к новым

 lc->Right() = np->Left();

 np->Left() = lc;

 p->Left() = np->Right();

 np->Right() = p;

 p = np;

}

 

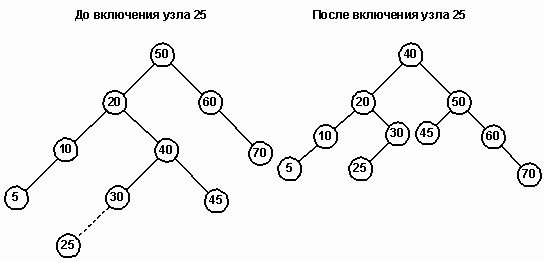
Двойной поворот иллюстрируется на дереве, изображенном на рисунке 17. Попытка вставить узел 25 разбалансирует корневой узел 50. В этом случае узел 20 (LC) приобретает слишком высокое правое поддерево и требуется двойной поворот.

Новым родительским узлом (NP) становится узел 40. Старый родительский узел становится его правым сыном и присоединяет к себе узел 45, который также переходит с левой стороны дерева.

Рис. 17.

 

Итераторы АВЛ - деревьев.

Сканирование узлов дерева более сложно, чем сканирование массивов и последовательных списков, так как дерево является нелинейной структурой и существует несколько способов прохождения дерева. Проблема каждого из них состоит в том, что до завершения рекурсивного процесса из него невозможно выйти. Нельзя остановить сканирование, проверить содержимое узла, выполнить какие-нибудь операции с данными, а затем вновь продолжить сканирование со следующего узла дерева.

Используя же итератор, клиент получает средство сканирования узлов дерева, как если бы они представляли собой линейный список, без обременительных деталей алгоритмов прохождения, лежащих в основе процесса. Наш класс использует класс Stack и наследуется от базового класса итератора. Поэтому сначала опишем класс Stack и базовый класс итератора.

Спецификация класса Stack.

Объявление:

 

#include <iostreani.h>

#include <stdlib.h>

 

const int MaxStackSize = 50;

 

class Stack

{

 private:

 DataType stacklist[MaxStackSize];

 int top;

 public:

 // конструктор; инициализирует вершину

 Stack(void);

 

 // операции модификации стека

 void Push(const DataType& item);

 DataType Pop(void);

 void ClearStack(void);

 

 // доступ к стеку

 DataType Peek(void) const;

 

 // методы проверки состояния стека

 int StackEmpty(void) const;

 int StackFull(void) const; // для реализации, основанной на массиве

};

 

Описание:

Данные в стеке имеют тип DataType, который должен определяться с использованием оператора typedef. Пользователь должен проверять, полный ли стек, перед попыткой поместить в него элемент и проверять, не пустой ли стек, перед извлечением данных из него. Если предусловия для операции push или pop не удовлетворяются, печатается сообщение об ошибке и программа завершается. StackEmpty возвращает TRUE, если стек пустой, и FALSE - в противном случае. Используйте StackEmpty, чтобы определить, может ли выполняться операция Pop.

StackFull возвращает TRUE, если стек полный, и FALSE - в противном случае. Используйте StackFull, чтобы определить, может ли выполняться операция Push. ClearStack делает стек пустым, устанавливая top = -1. Этот метод позволяет использовать стек для других целей.

Реализация класса Stack.

Конструктор Stack присваивает индексу top значение -1, что эквивалентно условию пустого стека.

 

//инициализация вершины стека

 

Stack::Stack (void): top(-l)

{ }

 

Операции стека.

Две основные операции стека вставляют (Push) и удаляют (Pop) элемент из стека. Класс содержит функцию Peek, позволяющую получать данные элемента, находящегося в вершине стека, не удаляя в действительности этот элемент. При помещении элемента в стек, top увеличивается на 1, и новый элемент вставляется в конец массива stacklist. Попытка добавить элемент в полный стек приведет к сообщению об ошибке и завершению программы.

 

// поместить элемент в стек

 

void Stack::Push (const DataTypes item)

{

 // если стек полный, завершить выполнение программы

 if (top == MaxStackSize-1)

 {

 cerr << "Переполнение стека!" << endl;

 exit(l);

 }

 // увеличить индекс top и копировать item в массив stacklist

 top++;

 stacklist[top] = item;

}

 

Операция Pop извлекает элемент из стека, копируя сначала значение из вершины стека в локальную переменную temp и затем увеличивая top на 1. Переменная temp становится возвращаемым значением. Попытка извлечь элемент из пустого стека приводит к сообщению об ошибке и завершению программы.

 

// взять элемент из стека

 

DataType Stack::Pop (void)

 DataType temp;

 

 // стек пуст, завершить программу

 if (top == -1)

 {

 cerr << "Попытка обращения к пустому стеку! " << end.1;

 exit(1);

 }

 

 // считать элемент в вершине стека

 temp = stacklist[top];

 

 // уменьшить top и возвратить значение из вершины стека

 top--;

 return temp;

}

 

Операция Peek в основном дублирует определение Pop с единственным важным исключением. Индекс top не уменьшается, оставляя стек нетронутым.

 

// возвратить данные в вершине стека

 

DataType Stack::Peek (void) const

{

 // если стек пуст, завершить программу

 if (top == -1)

 {

 cerr << "Попытка считать данные из пустого стека!" << end.1;

 exit(l);

 }

 return stacklist[top];

}

 

Условия тестирования стека.

Во время своего выполнения операции стека завершают программу при попытках клиента обращаться к стеку неправильно; например, когда мы пытаемся выполнить операцию Peek над пустым стеком. Для защиты целостности стека класс предусматривает операции тестирования состояния стека. Функция StackEmpty проверяет, является ли top равным -1. Если - да, стек пуст и возвращаемое значение - TRUE; иначе возвращаемое значение - FALSE.

 

// тестирование стека на наличие в нем данных

 

int Stack::StackEmpty(void) const

{

 return top == -1;

}

 

Функция StackFull проверяет, равен ли top значению MaxStackSize - 1. Если так, то стек заполнен и возвращаемым значением будет TRUE; иначе, возвращаемое значение - FALSE.

 

// проверка, не переполнен ли стек

 

int Stack::StackFuli(void) const

{

 return top == MaxStackSize-1;

}

 

Метод ClearStack переустанавливает вершину стека на -1. Это восстанавливает начальное условие, определенное конструктором.

 

// удалить все элементы из стека

 

void Stack::ClearStack(void)

{

 top = -1;

}

 

Стековые операции Push и Pop используют прямой доступ к вершине стека и не зависят от количества элементов в списке.

Алгоритм TreeSort.

Когда объект типа InorderIterator осуществляет прохождение дерева поиска, узлы проходятся в сортированном порядке и, следовательно, можно построить еще один алгоритм сортировки, называемый TreeSort. Этот алгоритм предполагает, что элементы изначально хранятся в массиве. Поисковое дерево служит фильтром, куда элементы массива копируются в соответствии с алгоритмом вставки в бинарное дерево поиска. Осуществляя симметричное прохождение этого дерева и записывая элементы снова в массив, мы получаем в результате отсортированный список. На рисунке 20 показана сортировка 8 - элементного массива.

 

#include "bstree.h"

#include "treeiter.h"

 

// использование бинарного дерева поиска для сортировки массива

template <class T>

 

void TreeSort(T arr[], int n)

{

 // бинарное дерево поиска, в которое копируется массив

 BinSTree<T> sortTree;

 int i;

 

 // вставить каждый элемент массива в поисковое дерево

 for (i=0; i<n; i++)

 sortTree.Insert(arr[i]);

 

 // объявить итератор симметричного прохождения для sortTree

 InorderIterator<T> treeSortIter(sortTree.GetRoot());

 

 // выполнить симметричное прохождение дерева

 // скопировать каждый элемент снова в массив

 i = 0;

 while (!treeSortIter.EndOfList())

 {

 arr[i++] = treeSortIter.Data();

 treeSortIter.Next();

 }

}

 

Рис. 20.

 

Текст программы.

 

#pragma once

 

template <typename KEY,typename VALUE> class AvlTree

{

 

public:

    KEY key;

    VALUE value;

    int balance;

    AvlTree<KEY, VALUE>* left;

 AvlTree<KEY, VALUE>* right;

 bool empty;//заполнены ключ и значение или нет

 

    AvlTree()

    {

              empty=true;

              left = NULL;

              right = NULL;

              balance = 0;

    }

 

    AvlTree(KEY Key,VALUE Value)

 {

              empty=false;

 key = Key;

 value = Value;

 left = NULL;

 right = NULL;

 balance = 0;

 }

 

    int add(KEY Key, VALUE Value)//добавление узла, возвращает изменился баланс(1) или нет (0)

    { //при добавлении в правую ветку баланс узла увеличиваю на результат добавления

              if (empty)                          //в левую уменьшаю

              {                                                  //после каждого вызова add(...) вызываю TurnAround();

                       key = Key;               //дерево перестраивается пока потомок текущего узла в нужном направлении не будет NULL

                       value = Value;          //потом в этого потомка записываем новые значения

                       empty=false;

                       return 0;

              }

              if (Key == key)

                       throw CString(L"Уже есть");

              int a = balance;

              if (Key > key)

              {

                       if (right!= NULL)

                       {

                                 balance += right->add(Key, Value);

                                 TurnAround();

                       }

                       else

                       {

                                 right = new AvlTree<KEY, VALUE>(Key, Value);

                                 balance++;

                       }

              }

              else

              {

                       if (left!= NULL)

                       {

                                 balance -= left->add(Key, Value);

                                 TurnAround();

                       }

                       else

                       {

                                 left = new AvlTree<KEY, VALUE>(Key, Value);

                                 balance--;

                       }

              }

              if (balance!= a)

              {

                       return 1;

              }

              else

              {

                       return 0;

              }

    }

 

    void TurnAround()  //нормализация дерева, если баланс не равномерный смещаю(поворачиваю) узел так,

    {                                        //чтобы количество потомков справа и слева не отличалось больше, чем на 1

              if (balance == 2)

              {

                       if (right->balance >= 0)

                       {

                                 KEY tKey = key;

                                 VALUE tValue = value;

                                 key = right->key;

                                 value = right->value;

                                 right->key = tKey;

                                 right->value = tValue;

                                 AvlTree<KEY, VALUE>*tNode=right->right;

                                 right->right = right->left;

                                 right->left = left;

                                 left = right;

                                 right = tNode;

                                 balance = left->balance - 1;

                                 left->balance = 1 - left->balance;

                       }

                       else

                       {

                                 KEY tKey = key;

                                 VALUE tValue = value;

                                 key = right->left->key;

                                 value = right->left->value;

                                 right->left->key = tKey;

                                 right->left->value = tValue;

                                 AvlTree<KEY, VALUE>* tNode = right->left->right;

                                 right->left->right = right->left->left;

                                 right->left->left = left;

                                 left = right->left;

                                 right->left = tNode;

                                 balance = 0;

                                 right->balance = (left->balance == -1)? (1): (0);

                                 left->balance = (left->balance == 1)? (-1): (0);

                       }

              }

              else

              {

                       if (balance == -2)

                       {

                                 if (left->balance <= 0)

                                 {

                                          KEY tKey = key;

                                          VALUE tValue = value;

                                          key = left->key;

                                          value = left->value;

                                          left->key = tKey;

                                          left->value = tValue;

                                          AvlTree<KEY, VALUE>* tNode = left->left;

                                          left->left = left->right;

                                          left->right = right;

                                          right = left;

                                          left = tNode;

                                          balance = 1 + right->balance;

                                          right->balance = -1 - right->balance;

                                 }

                                 else

                                 {

                                          KEY tKey = key;

                                          VALUE tValue = value;

                                          key = left->right->key;

                                          value = left->right->value;

                                          left->right->key = tKey;

                                          left->right->value = tValue;

                                          AvlTree<KEY, VALUE>* tNode = left->right->left;

                                          left->right->left = left->right->right;

                                          left->right->right = right;

                                          right = left->right;

                                          left->right = tNode;

                                          balance = 0;

                                          left->balance = (right->balance == 1)? (-1): (0);

                                          right->balance = (right->balance == -1)? (1): (0);

                                 }

                       }

              }

    }

 

    typename AvlTree<KEY, VALUE>* getNode(KEY Key)//поиск узла по ключу

    {

              AvlTree<KEY, VALUE>* node=this;

              while (true)

              {

                       if (node == NULL)

                                 throw CString(L"Не найдено");

                       if (node->key == Key)

                                 return node;

                       if (node->key < Key)

                       {

                                 node = node->right;

                       }

                       else

                       {

                                 node = node->left;

                       }

     

              }

    }

 

        

               int remove(KEY Key,AvlTree<KEY, VALUE>*parent=NULL) //удаление узла, перемещаюсь по дереву, по ключу

 {                                                                                                                 //при прохождении узла опять меняю баланс в зависимости от направления и поворачиваю его TurnAround()

 int a = balance;                                                                                   // как дошел до нужного узла перемещаю его, пока оба его потомка не будут NULL

 if (key == Key)                                                                                   // и удаляю

 {

                        

 if (right == NULL && left == NULL)

 {

                                  if(parent->left->key==this->key)

                                  {

                                           parent->left=NULL;

                                  }

                                  else

                                  {

                                           parent->right=NULL;

                                  }

 return 1;

 }

 else

 {

 if (balance >= 0)

 {

 

 if (right!= NULL)

 {

 AvlTree<KEY, VALUE>* tNode = right;

 while (tNode->left!= NULL)

 {

 tNode = tNode->left;

 }

 KEY tKey = key;

 VALUE tValue = value;

 key = tNode->key;

 value = tNode->value;

 tNode->key = tKey;

 tNode->value = tValue;

 balance -= right->remove(Key,this);

 }

 

 }

 else

 {

 

 if (left!= NULL)

 {

 AvlTree<KEY, VALUE>* tNode = left;

 while (tNode->right!= NULL)

 {

 tNode = tNode->right;

 }

 KEY tKey = key;

 VALUE tValue = value;

 key = tNode->key;

 value = tNode->value;

 tNode->key = tKey;

 tNode->value = tValue;

 balance += left->remove(Key,this);

 }

 

 }

 }

 }

 else

 {

 if (Key > key)

 {

 if (right!=NULL)

 {

 balance -= right->remove(Key,this);

 TurnAround();

 }

 else

 {

 throw CString("Не найдено");

 }

 }

 else

 {

 if (left!=NULL)

 {

 balance += left->remove(Key,this);

 TurnAround();

 }

 else

 {

 throw CString("Не найдено");

 }

 }

 }

 if (balance!= a)

 {

 return (balance == 0)? (1): (0);

 }

 else

 {

 return 0;

 }

 }

 

 

    ~AvlTree()

    {

                  

    }

};

 

СПИСОК ЛИТЕРАТУРЫ

 

1. Каррано Ф.М., Причард Дж.Дж. К26 Абстракция данных и решение задач на С++ - I -. Стены и зеркала, 3-е издание.: Пер.с англ. - М.: Издательский дом «Вильяме», 2003. - 848 с: ил. - Парал. тит. англ.

2. Ж.-Л. Лорьер. Системы искусственного интеллекта. – М.: Мир, 1991.

3. Бабэ Б. Просто и ясно о Borland С++: пер. с англ. – СПб.: Питер, 1997. – 464 с.

4. Ирэ П. Объектно – ориентированное программирование с использованием С++: пер. с англ. К.: НИПФ ДиаСофтЛтд, 1995. – 480 с.

5. Пр