Методи логічно дидактичних ігор на уроках геометрії

У сучасній дидактиці існують різні класифікації уроків, залежно від взятих за основу ознак [8]:

1. За способами їх проведення виділяють: уроклекція, кіноурок, урокбесіда, урокпрактичне заняття, урокекскурсія, урок самостійної роботи учнів у класі, урок лабораторної роботи;

2. За загальнопедагогічною метою організації занять: урок вивчення нового матеріалу; удосконалення знань, умінь і навичок; контролю та корекції знань, умінь і навичок.

3. Залежно від дидактичної мети: спеціалізований урок (переважає одна мета), комбінований (дві або більше рівнозначні мети). Різновидами спеціалізованого уроку є: урок засвоєння нових знань; урок засвоєння умінь та навичок; урок застосування знань, умінь та навичок; урок контролю та корекції знань, умінь та навичок; урок узагальнення та систематизації знань.

Сучасним методом навчання і виховання, що сприяє оптимізації та активізації навчального процесу та дозволяє показати цікаві й захоплюючі грані математики, є дидактична гра.

Дидактична гра – це вид діяльності, залучившись до якої, діти навчаються. Поєднання навчальної спрямованості та ігрової форми дозволяє стимулювати невимушене оволодіння конкретним навчальним матеріалом.

Дидактична гра має чітку структуру, що вирізняє її зпоміж іншої діяльності. Основні структурні компоненти дидактичної гри: ігровий задум, правила, ігрові дії, пізнавальний зміст або дидактичне завдання, обладнання, результат гри.

На відміну від ігор взагалі дидактична гра має суттєву ознаку – наявність чітко визначеної мети навчання і відповідного їй педагогічного результату, що можуть бути обґрунтовані, подані наочно і характеризуються пізнавальною спрямованістю.

Ігровий задум – перший структурний компонент гри, закладений у дидактичне завдання, що необхідно виконати під час навчання. Ігровий задум найчастіше виступає у; вигляді питання або загадки, що ніби проектує хід гри. Це надає грі пізнавального характеру, висуває до її учасників певні вимоги щодо знань.

Суттєвими в дидактичній грі є дії, що регламентуються правилами гри, сприяють пізнавальній активності учнів, надають їм змогу виявити свої здібності, застосувати наявні знання, вміння і навички для досягнення цілей гри. Дуже часто ігровим діям передує розв'язання задачі.

Основою дидактичної гри є пізнавальний зміст, що полягає у засвоєнні тих знань і вмінь, які застосовуються під час розв'язування навчальної проблеми, поставленої грою. Цінність дидактичної гри полягає в тому, що діти, граючи, значною мірою самостійно набувають нових знань, активно допомагаючи одне одному.

Математичний бік змісту гри завжди повинен чітко висуватися на перший план. Лише за цієї умови гра буде виконувати свою роль у математичному розвитку школярів і вихованні їх інтересу до математики.

Під час організації дидактичних ігор математичного змісту перш за все необхідно продумати і врахувати такі питання методики:

1.Мета гри. Які математичні вміння й навички учні засвоять у ході гри? Якому моменту гри слід приділити особливу увагу? Які інші виховні цілі передбачити під час проведення гри?

2.Визначення кількості гравців. Кожна гра потребує певної мінімальної або максимальної кількості учасників. Це слід враховувати під час організації гри.

3.Добирання дидактичних матеріалів і посібників, що знадобляться для гри.

4.Продумування питання найменшої витрати часу для ознайомлення учнів з правилами гри.

5.Визначення тривалості гри.

6.Планування засобів забезпечення участі всіх школярів у грі.

7.Спостереження за учнями під час гри.

8.Передбачення можливих змін, що доведеться внести у хід гри, щоб підвищити зацікавленість і активність учнів.

9.Планування висновків, про які необхідно повідомити учнів по завершенні гри (найвдаліші моменти, недоліки, що трапилися у ході гри, результат засвоєння математичних знань, оцінювання учасників гри, зауваження щодо порушення дисципліни тощо).

Дидактичні ігри добре поєднуються із серйозним навчанням. Включення в урок дидактичної гри та ігрових моментів призводить до того, що процес навчання стає цікавим і захоплюючим, створює бадьорий, спрямований на роботу настрій в учнів, перетворює подолання труднощів на успішне засвоєння навчального матеріалу. Дидактичні ігри слід розглядати як один із видів творчої діяльності, що тісно пов'язаний з іншими видами навчальної роботи.

Дидактичні ігри на уроках математики мають включати: 1) об'єкт моделювання, введення в дидактичну гру; 2) опис основних способів взаємодії учасників гри; 3) правила взаємодії суб'єктів гри; 4) список командучасниць; 5) розподіл ролей і функцій учасників дидактичної гри; 6) інструкцію кожному учаснику або кожній команді щодо участі в грі; 7) загальну схему (етапи) проведення гри; 8) модифікацію; 9) способи, умови і критерії підбиття підсумків гри

Дослідники виділяють шість основних груп умов ефективності застосування дидактичних ігор на уроках геометрії в 79х класах основної школи: 1) умови, що забезпечують формування соціальної і пізнавальної активності як ключових особистісних характеристик підлітка; 2) умови, що забезпечують розвиток самостійності учнів: діалогова організація діяльності у процесі гри, наявність кінцевого та проміжних результатів на різних стадіях гри, варіативність вибору завдань та початкових умов; 3) умови, що забезпечують розвиток здатності до самореалізації та саморегуляції навчальної діяльності підлітків у процесі гри; 4) умови, що забезпечують гармонійну індивідуальність особистості підлітка; доцільне співвідношення образного і логічного компонентів мислення, рівня пізнавальних потреб та можливостей щодо їх реалізації під час виконання завдань гри; розумне поєднання емоційного і раціонального під час навчання; 5) умови, що забезпечують узгодженість особистих прагнень підлітків з суспільнокорисною спрямованістю їх діяльності; 6) умови, що забезпечують доцільне поєднання педагогічного керівництва і самостійної діяльності учнів, раціональне співвідношення безпосереднього і опосередкованого впливів педагога та колективу на учня.

Результати дослідження вказують на те, що під час організації дидактичних ігор на уроках геометрії в 79х класах необхідно дотримуватися таких положень: 1) правила гри мають бути простими, чітко сформульованими, а математичний зміст матеріалу – доступний розумінню учнів; 2) завдання гри повинні містити достатню кількість інформації для активної мислительної діяльності підлітків на уроці, що забезпечуватиме досягнення розвивальної та навчальної цілей уроку; 3) дидактичний матеріал, який використовується в процесі гри, має бути цікавим, педагогічно доцільним і зручним у користуванні; 4) якщо дидактична гра має характер змагання, то слід забезпечити справедливий і об'єктивний контроль її результатів; 5) кожен учень має бути активним учасником дидактичної гри; 6) якщо на уроці геометрії створюється кілька ігрових ситуацій, то їх варто чергувати за складністю математичного матеріалу, що до них входить, або характером розумових дій, які необхідні для їх виконання; якщо на кількох уроках підряд проводяться дидактичні ігри, які вимагають аналогічних мислительних дій від учнів, то за змістом математичного матеріалу вони мають задовольняти принцип: від простого до складного, від конкретного до абстрактного; 7) необхідно дотримуватися міри використання дидактичних ігор у навчанні, щоб підлітки не звикли в усьому бачити тільки гру; 8) під час дидактичної гри від учнів слід вимагати чіткого і грамотного вираження своїх думок, проведення послідовних логічних міркувань, обґрунтовування висновків; 9) дидактична гра буде результативнішою, якщо вона закінчиться на тому самому уроці, на якому і розпочалася

Найбільш ефективними для учнів 79х класів на етапі вивчення нового матеріалу з алгебри та геометрії виявилися такі дидактичні ігри: в процесуальному аспекті за рівнем пізнавальної самостійності – конструктивні і творчі, за логікою чергування кроків гри – традуктивні, за часом перебігу – довготривалі, ділові; в управлінському аспекті за способом визначення результатів – вільні, за формою проведення гри – колективні або групові; в соціальнопсихологічному аспекті за характером ігрового процесу – стратегічні, за включенням виду гри в навчання – художні, загадкововиграшні, за збігом цілей та інтересів суб'єктів гри – спільні за цілями, інтереси можуть збігатися, а можуть бути різними.

Класичним прикладом дидактичної геометричної гри освоєнні теми „Рівновеликість та рівноскладеність багатокутників” є древня китайська головоломка «Танграм” [5], яка виникла в Китаї 4 тис.років тому. Головоломка представляє собою квадрат 12*12 квадратів, які розрізаються на 7 окремих багатокутників 5 трикутників, 1 квадрат та 1 паралелограм (рис.2.1).

Рис. 2.1. Побудова структурних багатокутників головоломки „танграм”

Рис. 2.2. Декілька складених фігурок багатокутників з 7 елементів головоломки „танграм”

Рис. 2.3. Розшифрування техніки складання фігурок багатокутників на рис.2.2 за допомогою елементів „танграма”

Рис. 2.4. Рівновеликі та рівноскладені багатокутники з 7 елементів елементарних багатокутників головоломки „танграм”

 

 

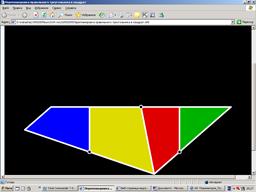
Рис. 2.5. Приклад комп'ютерного демонстраційно – дидактичного матеріалу „Перетворення рівноскладених та рівновеликих багатокутників (рівнобічний трикутник у квадрат)”[2]

 

РОЗДІЛ 3