
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логічне мислення та його складовіСодержание книги
Поиск на нашем сайте
КУРСОВА РОБОТА з дисципліни “Педагогіка” на тему: „Розвиток логічного мислення учнів у процесі вивчення геометрії”
ЗМІСТ
ВСТУП РОЗДІЛ 1 ЛОГІЧНЕ МИСЛЕННЯ ТА ЙОГО СКЛАДОВІ 1.1 Логіка як наука про мислення 1.2 Поняття як перший ступінь логічних форм мислення 1.3 Судження як другий ступінь логічних форм мислення 1.4 Умовивід як третій ступінь логічних форм мислення 1.5 Основні закони логіки мислення РОЗДІЛ 2 ВПЛИВ ВИБОРУ МЕТОДІВ НАВЧАННЯ НА РОЗВИТОК ЛОГІЧНОГО МИСЛЕННЯ УЧНІВ У ШКОЛІ 2.1 Традиційні методи навчання та їх класифікація 2.2 Класифікація методів проблемнорозвиваючого навчання 2.3 Методи логічнодидактичних ігор на уроках геометрії РОЗДІЛ 3 РОЛЬ ОСНОВНИХ ЕЛЕМЕНТІВ ШКІЛЬНОГО УЧБОВОГО ПРОЦЕСУ ВИВЧЕННЯ ГЕОМЕТРІЇ У РОЗВИТКУ ЛОГІЧНОГО МИСЛЕННЯ УЧНІВ 3.1 Роль геометричних означень та понять 3.2 Роль логічних доведень геометричних тверджень(лем та теорем) 3.3 Роль практичного розв’язування геометричних задач ВИСНОВКИ СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ ДОДАТКИ ВСТУП
Відомо, що людина відрізняється від інших живих істот своїм умінням мислити, думати. Мислення – це вища форма пізнання світу. Свої думки людина виражає за допомогою мови. Навіть тоді, коли людина міркує „про себе”, вона неодмінно оформляє думки словами. Психологи називають це внутрішньою мовою. Всебічні дослідження привели вчених до висновку, що мислення і мова становлять нерозривну єдність. Якщо ж проаналізувати мову довільної групи людей, то можна помітити, що вона не однакова: одні люди виражають свої думки лаконічно, чітко, зрозуміло, обгрунтовано, інші – розпливчасто, не завжди зрозуміло. Про перших часто говорять, що вони мислять логічно, про других цього сказати не можна. Звичайно, кожний з нас хотів би мислити логічно. Слово „логічно” походить від терміна „логіка”. Логікаце наука про форми і закони мислення. Хоч мислення має надзвичайно складну структуру, стародавні мислителі помітили, що значну частину умовиводів (висновків) ми робимо за стандартними схемами, незалежними від того конкретного матеріалу, яким оперуємо. Так, закон силогізму, яким ми часто користаємося, твердить: „з істиності тверджень „ Близько 2,5 тисячі років тому в Індіїї, Китаї і Греції мислителі й філософи почали систематично вивчати загальні форми логічних умовиводів. Особливо вплинула на формування логіки як науки і на її дальший розвиток давньогрецька формальна логіка, розвинута Платоном, Арістотелем і стоїками. Велике значення для її розвитку мали праці великого грецького мислителя Арістотеля (384322 рр. до н.е.), в яких він показав що правильні міркування підпорядковані невеликій кількості законів, які не залежать від змісту висловлень, а тільки від їх форми. Тому традиційну, Арістотелеву, логіку називають ще формальною, а Арістотеля вважають батьком формальної логіки. Він розвинув її настільки фундаментально, що багато століть вона залишалась неперевершеним зразком логічного аналізу. У 17 столітті видатний німецький учений Г.Лейбниц (16461716) чітко сформулював ідею побудови нової логіки, в якій би кожному поняттю відповідав певний символ, а міркування мали б форму обчислень. Проте його праці містили лише програму побудови так званої символічної логіки. Тільки в середині 19 століття англійский математик Д. Буль (18151864) частково втілив у життя ідею Лейбница: він створив алгебру логіки, в якій діють закони, подібні до законів звичайної алгебри, але буквами позначаються не числа, а висловлення. Великий внесок у розвиток математичної логіки зробили вчені різних країн: німці Г. Фреге (18481925), Д. Гільберт (18621943), австрієць К. Гедель (народився в 1906 р.), англійці А де Морган (18061871), А. Уайтхед (18611947), Б. Рассел (18721970), поляки Я. Лукасевич (18781956), А. Тарський (19011983), американці А. Черч (народився в 1903 р.), А. Тьюрінг (19121954), італієць Д.Пеано (18581932), росіянин П.С.Порецький (18461907), радянські математики П.С.Новиков (19011975), А.А. Марков (19031980), А.М. Колмогоров (19031987) та інші. Математична логіка уточнила й поновому висвітлила поняття і методи традіційної формальної логіки, істотно розширила її можливості й сферу застосування. Нині математична логіка використовується в біології, медицині, лінгвістиці, педагогіці, психології, економіці, техніці, не говорячи вже про саму математику. Надзвичайно важлива роль належить математичній логіці в розвитку обчислювальної техніки: вона використовується в конструюванні електроннообчислювальних машин (ЕОМ) і при розробці штучних мов для спілкування з машинами. Метою дійсної курсової роботи було дослідження шляхів побудови програм навчання курсу геометрії в школі з погляду виховання логічного мислення учнів. РОЗДІЛ 1 РОЗДІЛ 2 РОЗДІЛ 3 МИСЛЕННЯ УЧНІВ Рис. 3.1
Сформульоване твердження виражає ознака (перпендикулярність двох прямих до третьої прямої), по якому можна зробити висновок про паралельність двох прямих, або, коротко говорячи, ознака паралельності двох прямих. 2. Про січну паралельних прямих і утворених нею кутах Нехай a і b дві паралельні прямі й Січна утворить із паралельними прямими дві пари внутрішніх одностронних і дві пари внутрішніх навхрест лежачих кутів.
Рис.3.2
Нехай відповідні кути Нехай сума однобічних кутів 3. Означеннях прямокутника, трикутника, паралелограма й трапеції Приведемо означення прямокутника, трикутника, паралелограма й трапеції. Означення. Параллелограм це чотирикутник, у якого протилежні сторони рівні й паралельні, тобто лежать на паралельних прямих. Означення.Прямокутник це параллелограм, у якого всі кути прямі. Означення.Трапецією називається чотирикутник, у якого тільки дві протилежні сторони паралельні. Ці паралельні сторони називаються основагиями трапеції. Дві інші сторони називаються бічними сторонами. Означення.Трикутником називається фігура. яка складається із трьох крапок, що не лежать на одній прямій, і трьох відрізків, попарно з'єднуючі ці точки. Точки називаються вершинами трикутника, а відрізки сторонами. 4. Про площу прямокутника Теорема. Площа прямокутника зі сторонами
На підставі вищевикладених аксіом і теорем, доведемо теореми про площі елементарних багатокутників методом рівновеликих і рівноскладених елементів багатокутників. а) Площа паралелограма Теорема. Площа паралелограма дорівнює добутку його основи на висоту. Довести: SABCD=AD x BH Доведення 1. Перекроїмо паралелограм у прямокутник. Для цього розріжемо його по висоті BH, і трикутник ABH прикладемо праворуч як показано на рис.3.3. Одержимо прямокутник HBCH1, рівноскладений з паралелограмом ABCD. Але рівноскладені фігури є рівновеликими, тобто SHBCH1=SABCD. 2. SHBCH1=BC x BH. Але BC=AD по властивості паралелограма. Тоді SABCD=AD x BH. Теорема доведена.
Рис.3.3 Дано: ABCDПаралелограм, ADпідстава, BHВисота б) Площа трикутника Теорема. Площа трикутника дорівнює половині добутку основи на висоту.
Рис.3.4. Дано: ABCТрикутник, AC основа, BH висота
Довести: SABC =? AC x BH Доведення Перекроїмо трикутник у паралелограм. Для цього проведемо середню лінію MN і розріжемо трикутник ABC на дві частини. Трикутник MNC прикладемо до відрізка BM як показано на рис.3.4. Одержимо паралелограм ABDN, рівноскладений із трикутника ABC, а отже й рівновеликий. Тоді SABDN=SABC
SABDH=AN x BH. Але AH=1/2 AC
тому що NСередина AC. Отже SABC=1/2 AC x BH. Теорема доведена. в) Площа трапеції Теорема. Площа трапеції дорівнює добутку напівсуми її підстав на висоту.
Рис.3.5 Дано: ABCDТрапеція, AD і BC основи, BHВисота
Довести: SABCD=1/2 (AD + BC) x BH Доведення Перекроїмо трапецію в трикутник. Для цього розріжемо її по відрізку BM, де M середина сторони CD.Трикутник BCM прикладемо до відрізка MD як показано на рис.3.5. Одержимо трикутник ABN рівноскладений із трапецією ABCD, а отже й рівновеликий, тобто SABN=SABCD
SABN=1/2 AN x BH, (3.1)
Але AN =AD + DN, а DN = BC. Звідки AN=AD + BC. Підставимо в (3.1), одержимо SABCD=1/2 (AD + BC) x BH. Теорема доведена. г) Розрахунок площі несиметричного п'ятикутника методом побудови рівновеликого трикутника (рис.3.6). Дано довільний 5кутник
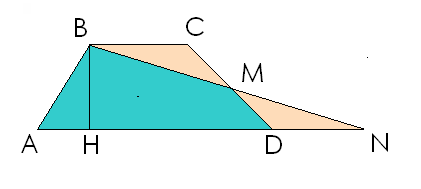
Рис.3.6 Перебудова п’ятикутника в равновеликий трикутник
Перебудовуємо його в рівновеликий трикутник: 1.Будуємо діагональ AC, з'єднуючи точки A й C усередині багатокутника 2.Продовжуємо по стороні AE пряму FK 3.Через точку B будуємо пряму BF, що паралельна діагоналі AC. 4.Із точки C в точку F перетинання прямих BF і FK проводимо відрізок CF 5.Оскільки їхні висоти однакові й дорівнюють відстані по перпендикуляру між паралельними прямими; площі цих трикутників рівні, оскільки розраховуються як половина добутку висоти трикутника на його основу. 6.Через точки С й Eпроводимо другу діагональ п'ятикутника. 7.Через точку D будуємо пряму DK паралельну другій діагоналі СE 8. Із точки C проводимо відрізок CK у точку K перетинання прямих DK і FK. 9.Трикутник CED і побудований трикутник CEK розташовані між паралельними прямими CE й DK мають загальну основу CE – рівновеликі, тобто мають рівну площу. 10.Отриманий трикутник
Рис. 3.7
Це можна зробити чотирма способами: на меншій стороні відкласти більшу від крапки З1 або від крапки В1 або на більшій відкласти меншу й знову відкладати як від крапки В1, так і від крапки А1. Якщо різниця буде біля крапки В1, то тоді дані не зв'язані між собою й не можна намітити план рішення. Якщо ж В1 А1 відкладемо від крапки В1 на В1С1, то дані: підстава, кут при підставах і різниця двох інших сторін – будуть зв'язані між собою, але й цей зв'язок не дає можливості намітити план рішення, вона недостатньо тверда, щоб побудувати, відновити фігуру Д2C1A1B1. Найкраще ввести різницю, відкладаючи B1D1 = B1C1, тому що в цьому випадку ми вже зможемо відновити фігуру З1А1Д1. Конкретизувавши в такий спосіб дані задачі, приступаємо до складання плану рішення. Побудувавши в довільної прямий відрізок, дорівнює підставі, одержимо дві вершини трикутника: А1 і З1. Знаючи кут З1А1У1, ми можемо знайти й положення крапки D1, де D1А1 = В1А1 – В1С1. Залишається розглянути, як побудувати крапку В1 знаючи положення крапки D1. Тому що З1У1 = В1D1, то крапка В1 равноудалена від крапок З1 і D1, тому вона повинна лежати на перпендикулярі Р1Q1, проведеному до відрізка З1D1 через його середину. Крапка перетинання прямій Р1Q1 і лучачи А1D1 і буде крапкою В1. Отже, приходимо до наступної побудови. На довільній прямій відкладаємо відрізок, дорівнює підставі, і будуємо кут, рівний даному, одна зі сторін якого містить побудований відрізок, а вершина збігається з кінцем цього відрізка. На другій стороні кута відкладаємо відрізок, рівний різниці двох інших сторін трикутника, і будуємо геометричне місце крапок, равноудаленных від відповідних кінців підстав і побудованого відрізка. Крапку перетинання цього геометричного місця зі стороною кута, що містить різниця, з'єднуємо з кінцем підставі й одержуємо шуканий трикутник. Із цього приклада видно, що при відшуканні рішення задачі на побудову, як і для арифметичних задач, застосовується аналітикосинтетичний метод. Після того як фігура побудована, необхідно встановити, чи задовольняє вона умовам задачі, тобто показати, що фігура, отримана з даних елементів певною побудовою, задовольняє всім умовам задачі. Виходить, доказ істотно залежить від способу побудови. Ту саму задачу можна вирішувати різними способами, залежно від наміченого при аналізі плану побудови, а тому, і доказ у кожному випадку буде своїм. Розглянемо задачу: «Побудувати трапецію по чотирьох сторонах» (рис.3.8).
Рис. 3.8
Провівши СК||ВА, рішення задачі зводимо до побудови трикутника КС по трьох сторонах: дві дорівнюють бічним сторонам трапеції (АК = КС), а КD = АD – ВР. Побудуємо трикутник КС, і, уважаючи сторону АD побудованої, доповнимо його до трапеції різними способами: 1) Проведемо ВС||А і, відклавши меншу підставу, з'єднаємо отриману крапку В с А Доказ зведеться до встановлення рівності: АВ = КС. 2) Якщо провести АВ||КС і ВС||А, те тоді вже треба довести, що АВ = КС і ВР = АК. 3) Якщо провести пряму СВ||DА й на ній знайти крапки В и В1, що відстоять від А на відстані, рівній бічній стороні, то в цьому випадку крапка В1 буде сторонньої й лише крапка В буде шуканої, причому доказ (ВР = АК) уже ускладнюється. 4) Якщо відшукувати крапку В, як крапку перетинання окружностей (А; АВ) і (З; СВ), те із двох крапок У и В2 тільки крапка В буде шуканою. Третій і четвертий випадки підкреслюють необхідність доказу. В аналізі ми знаходимо необхідні умови, яким повинне підкорятися побудова, щоб одержати шукану фігуру. Треба ще встановити, що знайдені необхідні умови є й достатніми, тобто, що побудована фігура задовольняє всім вимогам задачі. ВИСНОВКИ Логічне мислення – це вивчення об’єкту чи явища природи поступово за моделю > “ознаки та поняття “ >” судження” > ” умовивід” з використанням 4х основних законів логіки: закону тотожності, закону суперечності; закону третього і закону достатньої підстави. Структура геометрії – найбільш наближена до наведеного алгоритму логічного мислення, тому вивчення геометрії в шкільному курсі є процесом формування логічного типу мислення у учнів. Взірцем учбового курсу геометрії з позицій логічного розвитку учнів є “Начала” Евкліда, в яких викладені основи планіметрії, стереометрії й арифметики. Головна особливість “Начал” у тому, що вони побудовані за єдиною логічною схемою, яку розробив Арістотель (384–322 рр. до н. е.). Геометричне твердження за Евклідом, якщо воно повне, складається із шести логічно пов’язаних частин: 1) формулювання в загальних виразах; 2) постановка, яка відзначає конкретні дані, як правило, зображені у вигляді фігури; 3) визначення або вказівка (діорисмос), в якій вказується, що треба зробити або довести; 4) побудова, до якої входять додатки, необхідні для доведення; 5) саме доведення; 6) висновок, який повертається до формулювання і так само висловлюється в загальних виразах. “Начала” починаються з означень, постулатів і загальних понять (п’ять постулатів і дев’ять аксіом), із яких Евклід розвинув всю геометричну систему виключно логічним шляхом на основі викладених 470 тверджень, побудованих чисто дедуктивним способом. Аналіз сучасних підручників геометрії у школі показує, що потрібно ще раз повернутися до переробки системи викладання геометрії у школі, зосередивши послідовність викладення матеріалу у напрямку розвитку логічного мислення у учнів. При цьому, в підручниках необхідно ввести розділ „Логічна геометрія Евкліда”, оскільки вона, проіснувавши майже 2 тисячоліття, і в наш час є послідовним підручником для становлення системи логічного мислення.
Додаток А
Зміст навчального матеріалу та державні вимоги до рівня загальноосвітньої підготовки учнів [6]
Таблиця А.1 7й клас. ГЕОМЕТРІЯ
Таблиця А.2 8й клас. ГЕОМЕТРІЯ
Таблиця А.3 9й клас. ГЕОМЕТРІЯ
КУРСОВА РОБОТА з дисципліни “Педагогіка” на тему: „Розвиток логічного мислення учнів у процесі вивчення геометрії”
ЗМІСТ
ВСТУП РОЗДІЛ 1 ЛОГІЧНЕ МИСЛЕННЯ ТА ЙОГО СКЛАДОВІ 1.1 Логіка як наука про мислення 1.2 Поняття як перший ступінь логічних форм мислення 1.3 Судження як другий ступінь логічних форм мислення 1.4 Умовивід як третій ступінь логічних форм мислення 1.5 Основні закони логіки мислення РОЗДІЛ 2 ВПЛИВ ВИБОРУ МЕТОДІВ НАВЧАННЯ НА РОЗВИТОК ЛОГІЧНОГО МИСЛЕННЯ УЧНІВ У ШКОЛІ 2.1 Традиційні методи навчання та їх класифікація 2.2 Класифікація методів проблемнорозвиваючого навчання 2.3 Методи логічнодидактичних ігор на уроках геометрії РОЗДІЛ 3 РОЛЬ ОСНОВНИХ ЕЛЕМЕНТІВ ШКІЛЬНОГО УЧБОВОГО ПРОЦЕСУ ВИВЧЕННЯ ГЕОМЕТРІЇ У РОЗВИТКУ ЛОГІЧНОГО МИСЛЕННЯ УЧНІВ 3.1 Роль геометричних означень та понять 3.2 Роль логічних доведень геометричних тверджень(лем та теорем) 3.3 Роль практичного розв’язування геометричних задач ВИСНОВКИ СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ ДОДАТКИ ВСТУП
Відомо, що людина відрізняється від інших живих істот своїм умінням мислити, думати. Мислення – це вища форма пізнання світу. Свої думки людина виражає за допомогою мови. Навіть тоді, коли людина міркує „про себе”, вона неодмінно оформляє думки словами. Психологи називають це внутрішньою мовою. Всебічні дослідження привели вчених до висновку, що мислення і мова становлять нерозривну єдність. Якщо ж проаналізувати мову довільної групи людей, то можна помітити, що вона не однакова: одні люди виражають свої думки лаконічно, чітко, зрозуміло, обгрунтовано, інші – розпливчасто, не завжди зрозуміло. Про перших часто говорять, що вони мислять логічно, про других цього сказати не можна. Звичайно, кожний з нас хотів би мислити логічно. Слово „логічно” походить від терміна „логіка”. Логікаце наука про форми і закони мислення. Хоч мислення має надзвичайно складну структуру, стародавні мислителі помітили, що значну частину умовиводів (висновків) ми робимо за стандартними схемами, незалежними від того конкретного матеріалу, яким оперуємо. Так, закон силогізму, яким ми часто користаємося, твердить: „з істиності тверджень „ Близько 2,5 тисячі років тому в Індіїї, Китаї і Греції мислителі й філософи почали систематично вивчати загальні форми логічних умовиводів. Особливо вплинула на формування логіки як науки і на її дальший розвиток давньогрецька формальна логіка, розвинута Платоном, Арістотелем і стоїками. Велике значення для її розвитку мали праці великого грецького мислителя Арістотеля (384322 рр. до н.е.), в яких він показав що правильні міркування підпорядковані невеликій кількості законів, які не залежать від змісту висловлень, а тільки від їх форми. Тому традиційну, Арістотелеву, логіку називають ще формальною, а Арістотеля вважають батьком формальної логіки. Він розвинув її настільки фундаментально, що багато століть вона залишалась неперевершеним зразком логічного аналізу. У 17 столітті видатний німецький учений Г.Лейбниц (16461716) чітко сформулював ідею побудови нової логіки, в якій би кожному поняттю відповідав певний символ, а міркування мали б форму обчислень. Проте його праці містили лише програму побудови так званої символічної логіки. Тільки в середині 19 століття англійский математик Д. Буль (18151864) частково втілив у життя ідею Лейбница: він створив алгебру логіки, в якій діють закони, подібні до законів звичайної алгебри, але буквами позначаються не числа, а висловлення. Великий внесок у розвиток математичної логіки зробили вчені різних країн: німці Г. Фреге (18481925), Д. Гільберт (18621943), австрієць К. Гедель (народився в 1906 р.), англійці А де Морган (18061871), А. Уайтхед (18611947), Б. Рассел (18721970), поляки Я. Лукасевич (18781956), А. Тарський (19011983), американці А. Черч (народився в 1903 р.), А. Тьюрінг (19121954), італієць Д.Пеано (18581932), росіянин П.С.Порецький (18461907), радянські математики П.С.Новиков (19011975), А.А. Марков (19031980), А.М. Колмогоров (19031987) та інші. Математична логіка уточнила й поновому висвітлила поняття і методи традіційної формальної логіки, істотно розширила її можливості й сферу застосування. Нині математична логіка використовується в біології
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 391; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.115.139 (0.012 с.) |

 суть
суть 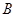 ” і „
” і „  ” випливає істинність твердження „
” випливає істинність твердження „  c третя пряма, що перетинає прямі a і b (рис.3.2). Пряма c стосовно паралельних прямих a і b називається січною.
c третя пряма, що перетинає прямі a і b (рис.3.2). Пряма c стосовно паралельних прямих a і b називається січною.
 1 і
1 і  дорівнює
дорівнює


 [3].
[3].
 й
й  побудовані між паралельними прямими й мають загальну основу, то
побудовані між паралельними прямими й мають загальну основу, то є рівноскладеним і рівновеликим п'ятикутнику
є рівноскладеним і рівновеликим п'ятикутнику  , оскільки:
, оскільки:




