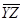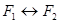Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доведення теоретико-математичних тотожностей і тверджень ⇐ ПредыдущаяСтр 4 из 4
Завдання: Довести тотожність: Доведення: 1) 2) 3) Побудова т аблиці істинності висловлень 4.1. Теоретичні відомості
Під висловленням розуміють пропозицію людської мови, про яку можна сказати, істинна вона або хибна. Пізніше стане ясно, чому тут говориться не про визначення, а про поняття висловлення. А надалі в нас з'явиться можливість дати точне визначення висловлення. Висловлення позначаються великими буквами латинського алфавіту, можливо з індексами: Задається дія заперечення за допомогою таблиці істинності:
Кон’юнкція задається за допомогою таблиці істинності:
Диз'юнкція задається за допомогою таблиці істинності:
Еквівалентність задається таблицею істинності:
Задається імплікація таблицею істинності:
Побудовання таблиці істинності висловлень
Завдання: Побудуйте таблиці істинності для висловлювання Відзначимо, відповідно до пріоритетів виконання операцій
Розв‘язок: Побудова диз'юнктивної нормальної форми (ДНФ) Теоретичні відомості Визначення. Нехай F – висловлення і
Визначення. Визначення. Кон’юнкція логічних змінних або їх заперечень називається елементарною кон’юнкцією. Загальний вигляд елементарної кон’юнкції
Визначення. Висловлення називається диз'юнктивною нормальною формою, якщо воно є диз'юнкцією елементарних кон’юнкцій. загальний вигляд ДНФ
де кожна
Теорема. Будь-яке висловлення рівносильне диз'юнктивній нормальній формі (говорять ще так: “Будь-яке висловлення зводиться до ДНФ”). Основні логічні тотожності: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) Тотожності, що містять константи: 17) 18) 19) 20) 21) 22) 23) 24) 25) 26)
5.2. Завдання:
Звести до ДНФ таке висловлювання. Розв‘язок: F=
Побудова досконалої диз'юнктивної нормальної форми (ДДНФ)
Теоретичні відомості
Визначення. Нехай Визначення. Нехай Визначення. Нехай Теорема. Якщо Визначення. Диз'юнктивна нормальна форма називається досконалою (ДДНФ), якщо всі складові її елементарної кон’юнкції є повними. Теорема. Нехай
6.2.Завдання: Звести до ДНФ таке висловлювання. Розв‘язок:
Графи Теоретичні відомості
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 109; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.88.130 (0.021 с.) |
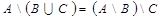 ;
;

 ;
; . Якщо висловлення А є істинним то пишуть А =1, інакше пишуть А =0.
. Якщо висловлення А є істинним то пишуть А =1, інакше пишуть А =0.












 ;
; , кроки, за якими буде побудована таблиця істинності висловлень:
, кроки, за якими буде побудована таблиця істинності висловлень:


 .
.
 у тому і тільки в тому випадку, коли
у тому і тільки в тому випадку, коли 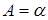 .
. .
. ,
, , у свою чергу, є елементарною кон’юнкцією.
, у свою чергу, є елементарною кон’юнкцією. – ідемпотентність диз'юнкції;
– ідемпотентність диз'юнкції; – ідемпотентність кон’юнкції;
– ідемпотентність кон’юнкції; – комутативність диз'юнкції;
– комутативність диз'юнкції; – комутативність кон’юнкції;
– комутативність кон’юнкції;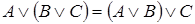 – асоціативність диз'юнкції;
– асоціативність диз'юнкції; – асоціативність кон’юнкції;
– асоціативність кон’юнкції; – дистрибутивність кон’юнкції щодо диз'юнкції;
– дистрибутивність кон’юнкції щодо диз'юнкції; – дистрибутивність диз'юнкції щодо кон’юнкції.
– дистрибутивність диз'юнкції щодо кон’юнкції. – перший закон Моргана.
– перший закон Моргана. – другий закон Моргана.
– другий закон Моргана. – закон подвійного заперечення.
– закон подвійного заперечення. – закон протиріччя.
– закон протиріччя. – закон виключення третіх.
– закон виключення третіх. .
. .
. .
. .
. .
. .
. .
.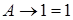 .
. .
. .
.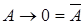 .
. .
. .
.



 – деяка множина логічних змінних. Елементарна кон’юнкція, в яку входять усі логічні змінні, називається повною елементарною кон’юнкцією щодо множини
– деяка множина логічних змінних. Елементарна кон’юнкція, в яку входять усі логічні змінні, називається повною елементарною кон’юнкцією щодо множини  .
. є повною елементарною кон’юнкцією щодо множини
є повною елементарною кон’юнкцією щодо множини  . Тоді
. Тоді  містить у таблиці істинності лише одну одиницю, причому на наборі
містить у таблиці істинності лише одну одиницю, причому на наборі 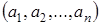 . І навпаки, якщо в таблиці істинності висловлення
. І навпаки, якщо в таблиці істинності висловлення  є лише одна одиниця на наборі
є лише одна одиниця на наборі  , то
, то  є повною елементарною кон’юнкцією, причому
є повною елементарною кон’юнкцією, причому – висловлення. Позначимо через
– висловлення. Позначимо через  множину всіх наборів
множину всіх наборів  , на яких
, на яких  .
.  називається множиною істинності висловлення
називається множиною істинності висловлення  . Можна записати, що
. Можна записати, що  .
. , то
, то  .
. – висловлення, що не є тотожно хибним, тобто
– висловлення, що не є тотожно хибним, тобто  ,тоді
,тоді
 ;
;