Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм програма множина графиСодержание книги
Поиск на нашем сайте
1. Доведення рівностей методом математичної індукції 2. Розробка алгоритму та написання програми обчислення множин 2.1. Теоретичні відомості 2.2. Проект обчислення 2.3. Організація структури програми 2.4. Вихідний текст програми 2.5.Опис процедур 2.5.1. Опис процедури SYS 2.5.1.1. Постановка задачі 2.5.1.2. Математична модель 2.5.1.3. Алгоритм рішення задачі 2.5.1.4. Блок-схема 2.5.2 Опис процедури OBED 2.5.3 Опис процедури PERET 2.5.4 Опис процедури RIZ 2.6. Результат 3. Доведення теоретико-математичних тотожностей і тверджень 4. Побудува таблиці істинності висловлень 4.1. Теоретичні відомості 4.2. Рішення 5. Побудова диз’юнктивної нормальної форми (ДНФ) 5.1. Теоретичні відомості 5.2. Рішення 6. Побудова досконалої диз’юнктивної нормальної форми (ДДНФ) 6.1. Теоретичні відомості 6.2.Рішення 7. Розробка алгоритму та написання програми знаходження множини елементарних циклів у графі 7.1. Теоретичні відомості
7.3. Блок-схема програми 7.4. Вихідний текст програми 7.5. Результат роботи програми Список літератури Доведення рівностей методом математичної індукції Теоретичні відомості ТЕОРЕМА. Нехай властивість Р вірна для п =1 і нехай з істинності Р для п = к випливає його істинність для п = к+1. Тоді властивість Р вірна для кожного ТЕОРЕМА. Нехай множина 1. 2. Для кожного Тоді ТЕОРЕМА (Зворотний метод математичної індукції). Нехай властивість р (n) виконується для n=1. з того, що вона вірна для кожного Зауваження. У загальному випадку індуктивний процес не зобов'язаний починатися з 1. Базисом індукції може бути будь-як ціле число a. ТЕОРЕМА. Нехай властивість р (n) виконується для n= a. З цього для кожного
Завдання 1: Довести, що для будь-якого
Розв‘язок: 1. Базиси індукції. Перевіримо рівність для п =1. Ліва частина = 2. Індуктивне припущення. Вважаємо рівність (1) вірною для п = к, тобто припустимо, що:
3. Індуктивний перехід. Доведемо рівність (1) для п=к+1, тобто доведемо, що: Таким чином на підставі методу математичної індукції рівність (1) вірна для кожного п. Розробка алгоритму та написання програми обчислення множин Теоретичні відомості Множина – це будь-яка певна сукупність об'єктів. Об‘єкти з яких складається множина, називаються його елементами. Множина, що не містить елементів, називається порожньою. Множини, як об’єкти, можуть бути елементами інших множин. Множини, елементи яких є множини, іноді називають сімейством. Сукупність об'єктів, які не є множиною, називають класом. Звичайно в конкретних міркуваннях елементи всіх множин беруться з деякого одного, достатньо широкої множини U яке називається універсальною множиною. Щоб задати множину, потрібно вказати, які елементи йому належать. Це можна зробити різними способами: - перерахунком елементів: М={a1,a2,…,ak}; - характеристичним предикатом: М={x| P(x)}; - породжуючою процедурою: M={x | x= f}. Розглянемо множини Y всіх множин, що не містять себе як елементу: Якщо множина Y існує, то ми повинні відповісти на наступне питання: Y 1. Обмежити використання характеристичні предикати вигляду: 2. Територія типів. Об‘єкти мають типи 0, множина елементів типу 0 мають тип 1, множина елементів типу 0 та 1 – типу 2 і т. д. Y не має типу і тому не може юути множиною. 3. Явна заборона приналежності множини самої собі: Множина А міститься у множині В якщо кожний елемент А є елементом В:
В цьому видатку А називається підмножиною В, В – над множиною А. З означенням Дві множини рівні, якщо вони є підмножинами один одного:
Кажуть, що кінцева множина А має потужність к, якщо вона рівно потужна відрізку 1..к
Операції над множинами
|
||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 180; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

 7.2. Алгоритм рішення задачі
7.2. Алгоритм рішення задачі .
. має такі властивості.
має такі властивості. .
. , якщо
, якщо  , то
, то  .
. .
. випливає, що р (n) вірна для n. Значить р (n) вірна для будь-якого натурального n.
випливає, що р (n) вірна для n. Значить р (n) вірна для будь-якого натурального n. випливає істинність для k +1. Значить р (n) істинно для будь-якого цілого
випливає істинність для k +1. Значить р (n) істинно для будь-якого цілого  .
. (1)
(1) , права частина =
, права частина =  . Тобто базис індукції виконується.
. Тобто базис індукції виконується. (2)
(2) ,звідси
,звідси  =
= 

 Y? Хай Y
Y? Хай Y 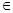 Y, тоді Y
Y, тоді Y  Y. Хай Y
Y. Хай Y  , де А – відома, явно існуюча множина (універсум). Звичайно при цьому використовується позначення
, де А – відома, явно існуюча множина (універсум). Звичайно при цьому використовується позначення  . Для Y універсум не вказаний, а тому Y множиною не може бути.
. Для Y універсум не вказаний, а тому Y множиною не може бути. - неприпустимий предикат. Відповідна аксіома називається аксіомою регулярності.
- неприпустимий предикат. Відповідна аксіома називається аксіомою регулярності.