Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамічна модель зубчастої передачі з двома ступенями свободиСодержание книги
Поиск на нашем сайте
Модель з числом ступенів свободи s=2 була утворена шляхом синтезу жорсткої моделі Генкин М.Д. [12], і Абрамов Б.М. [14]. Тут враховані наступні фактори [12]: - пружна деформація зубців; - сила непружнього опору, лінійно залежна від швидкості; - нормальній бічний зазор у зачепленні jn (рис. 5.1); - постійне передатне число; - сила тертя між зубцями.
Рисунок 5.2 – Нормальній бічний зазор у зачепленні jn Схема пружної моделі с двома ступенями свободи зображена на рисунку 5.3:
Рисунок 5.3 – Пружна динамічна модель зубчастої передачі
Кут повороту зубчастого колеса в абсолютному русі (в системі координат XO1Y) можна представити як суму двох кутів – кута повороту цього колеса разом з поворотною системою при умові недеформовані зубців и відносного кута повороту колеса в поворотній системі, обумовленим деформацією зубців під навантаженням:
У спільному випадку абсолютний рух зубчастих коліс досліджуваної передачі можна описати наступною системою диференціальних рівнянь:
де
Нормальна сила пружності між зубцями з урахуванням в’язкого опору и сили тертя визначають за наступними формулами:
де
Введення у формулу сили тертя відношення Коефіцієнт тертя для умов важко навантаженого контакту [14] Коефіцієнт непружнього опору
де
Коефіцієнт
де
де a – постійна величина [13, стр. 104]. Після підстановки виразів (5.5-5.6) в систему (5.2), диференціальні рівняння відносного руху зубів (тобто їх коливального руху) наберуть вигляду:
На підставі даних рівнянь складемо динамічну модель зубчастого зачеплення, що враховує вплив сил інерції, що виникають при зіткненні і пружній деформації зубів.
|
||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 194; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |



 (5.1)
(5.1) (5.2)
(5.2) і
і  - моменти інерції повідного і веденого коліс;
- моменти інерції повідного і веденого коліс; і
і  - зовнішні моменти, прикладені до коліс;
- зовнішні моменти, прикладені до коліс; - нормальна сила пружності між зубцями;
- нормальна сила пружності між зубцями;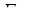 - сила тертя;
- сила тертя; - плече сили
- плече сили  - плече сили
- плече сили  - плече сили тертя, діючої на повідну ланку моделі;
- плече сили тертя, діючої на повідну ланку моделі; - плече сили тертя, діючої на ведену ланку моделі.
- плече сили тертя, діючої на ведену ланку моделі. (5.3)
(5.3) - коефіцієнт, що враховує вплив нормального бічного зазору;
- коефіцієнт, що враховує вплив нормального бічного зазору; - відносне переміщення зубів у напрямі нормалі до профілів в точці контакту в результаті пружної деформації;
- відносне переміщення зубів у напрямі нормалі до профілів в точці контакту в результаті пружної деформації;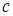 - жорсткість зубчастого зачеплення;
- жорсткість зубчастого зачеплення; - коефіцієнт непружного опору;
- коефіцієнт непружного опору;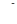 - коефіцієнт тертя між зубами;
- коефіцієнт тертя між зубами; - швидкість ковзання.
- швидкість ковзання. враховується зміна направлення сили тертя після проходження полюса зачеплення.
враховується зміна направлення сили тертя після проходження полюса зачеплення. .
. (5.4)
(5.4)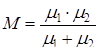 - приведені до основних кіл маси коліс;
- приведені до основних кіл маси коліс; - приведена маса провідної ланки;
- приведена маса провідної ланки; - приведена маса веденої ланки;
- приведена маса веденої ланки; - безрозмірний коефіцієнт демпфування, зазвичай
- безрозмірний коефіцієнт демпфування, зазвичай  ;
; за наступними умовами [12]. Надалі вважатимемо, що величини зовнішніх моментів, прикладених до коліс М1 і М2 залишаються в процесі зіткнення постійними, рівними їх статичним значенням. Залежно від значень з, враховуватимемо вплив сили інерції, що виникає при цьому, на кут повороту. Цю залежність можна виразити рівняннями:
за наступними умовами [12]. Надалі вважатимемо, що величини зовнішніх моментів, прикладених до коліс М1 і М2 залишаються в процесі зіткнення постійними, рівними їх статичним значенням. Залежно від значень з, враховуватимемо вплив сили інерції, що виникає при цьому, на кут повороту. Цю залежність можна виразити рівняннями: (5.5)
(5.5)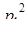 и
и  :
: (5.6)
(5.6) и
и  - жорсткість зубчастого зачеплення при однопарном і двухпарном зачепленні;
- жорсткість зубчастого зачеплення при однопарном і двухпарном зачепленні;