
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет функции передачи согласующей цепиСодержание книги Поиск на нашем сайте
Постановка задачи. Существует несколько способов формулировки задачи согласования, суть которых сводится к обеспечению заданного уровня передачи сигнала в ограниченной полосе частот. В каждом конкретном случае это требование может быть выражено в различной форме с различной степенью жесткости. Кроме того, это требование может быть дополнено другими требованиями ограничительного характера. В наиболее полной форме эти требования отражены в формулировке задачи, согласно которой исходно задана форма частотной характеристики коэффициента передачи (КСВ). Такая формулировка позволяет контролировать не только качество согласования в полосе согласования, но и избирательные свойства согласующей цепи. Такая формулировка отражает аппроксимационный характер задачи согласования, а в качестве аппроксимирующих функций используются приближения по Баттерворту, Чебышеву и Золотареву. Для расчета входного устройства целесообразно использовать полиномы Чебышева. Характеристика по Баттерворту - максимально плоская и везде монотонна. Функция Чебышева обеспечивает наилучшее приближение частотной характеристики к идеальной. В качестве функции передачи выберем функцию Чебышева 3-го порядка
где, Kpн - коэффициент передачи мощности Тn- полином Чебушева, имеющий порядок n=3уровень передачи мощности ε- коэффициент неравномерности Параметры ε и n определяются по заданным требованиям. Для перехода к полосовой функции передачи используем частотное преобразование
подставляя выражение (4.4) в (4.3) получим
График функции Kp(ω) представлен на рисунке 4.1. График имеет три экстремума это означает что функция Чебышева 3-го порядка.
Рисунок 4.1 - Функция передачи входного устройства
Функция передачи изначально не имеет нулей передачи в правой полуплоскости, поскольку все возможные виды частотных характеристик могут быть реализованы с использованием нулей на оси jω. Функция сопротивления на входе согласующей цепи Zвх(S) должна содержать в вещественной ее части сомножители s0=σ0
На основании выбранной частотной характеристики коэффициента передачи мощности и факторизации коэффициента отражения, связанного выражением
где ρ(ω) - коэффициент отражения на входе согласующей цепи, нагруженной на данное сопротивление нагрузки. Для нахождения коэффициента отражения воспользуемся программой Find в среде mathcad. В результате вычислений получили: δ =0.3366097 ε =0.2 a1=1.7544848=1.3591084=0.8=0.9156522=0.7106629=0.8=10= δ Рассчитанные коэффициенты образуют полиномы в соответствии с выражением
Исходная функция передачи (12) имеет двукратный нуль передачи в бесконечности. Поэтому для обеспечения условия совместимости коэффициент отражения необходимо дополнить сомножителем:
Входное сопротивление согласующей цепи с нагрузкой определим согласно выражению:
После подстановки и вычислений получили
Определение четных и нечетных частей полиномов функций сопротивлений:
|
||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 92; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.186.26 (0.005 с.) |

 , (4.1)
, (4.1) , (4.2)
, (4.2) (4.3)
(4.3) , (4.4)
, (4.4) . (4.5)
. (4.5)
 jω, имею- щийся в вещественной части сопротивления нагрузки. Для обеспечения этой совместимости используется коэффициент отражения Г(s), полученный в результате факторизации из коэффициента передачи мощности
jω, имею- щийся в вещественной части сопротивления нагрузки. Для обеспечения этой совместимости используется коэффициент отражения Г(s), полученный в результате факторизации из коэффициента передачи мощности . (4.6)
. (4.6) , (4.7)
, (4.7) . (4.8)
. (4.8) . (4.9)
. (4.9)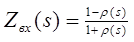 . (4.10)
. (4.10) .
. ;
; ;
; ;
; ;
;


