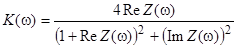Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет элементов согласующей цепиСодержание книги Поиск на нашем сайте
Исходными данными для расчета являются параметры согласуемой нагрузки. Нагрузка может быть задана либо в виде аналитической функции передачи, когда известна электрическая схема нагрузки, либо в форме измеренных параметров (сопротивление антенны, S-параметры транзисторов, измеренные на ряде частот). В последнем случае необходимо выбрать эквивалентную схему, описывающую с достаточной точностью сопротивление нагрузки. Согласуемым элементом является переключательный p-i-n диод из кремния. Он представляет собой трехслойный полупроводник, в котором между тонкими низкоомными (с большой концентрацией примесей) p- и n- слоями расположен промежуточный высокоомный i-слой чистого полупроводника, не содержащего объемного заряда. Толщина i-слоя составляет 0.02-0.5мм, поэтому емкость, создаваемая им, получается малой даже при относительно большой площади структуры и практически не зависит от смещения. Эквивалентная схема p-i-n диода, включенного в линию передачи с волновым сопротивлением R2 = 50 Ом, показана на рисунке 1.
Рисунок.4.2 - Эквивалентная схема нагрузки =15 Ом=50 Ом С=0.3 пФ Нормировка значений:
где ∆f =10 ГГц. В результате вычислений получили: R1=0.3; R2=1; C=0.942. Сопротивление нагрузки равно:
или в общем виде
где а0=R1+R2; a1=R1R2C; b1=R2C. Выражения для Zн (4.11) и (4.12) представляют собой билинейные функции, имеющие простой нуль передачи в правой полуплоскости. Определим четные и нечетные части полиномов функции (4.12): н=R1+R2=1.3 n1н=SR1R2C=0.2826Sн=1 n2н=SR2C= 0.942S
Определение нулей передачи нагрузки. Под нулями передачи понимают частоты, на которых отсутствует передача энергии от источника сигналов в нагрузку, расположенные в правой полуплоскости комплексной частоты класс - нули расположены в открытой правой полуплоскости класс - нули расположены в начале координат класс - нули расположены на мнимой оси класс - нули расположены в бесконечности Нули передачи в большинстве случаев можно определить непосредственно из эквивалентной схемы нагрузки. Для заданной нагрузки нули передачи расположены в правой полуплоскости, так как они определяются из равенства нулю функциин(-s2)=m1н m2н - n1нn2н, (4.13) составляющие которой определяются из сопротивления нагрузки
Подставляя значения составляющих Nн(-s2) из (4.12), находим
Таким образом, нуль передачи равен
В результате вычислений получили: Расчет z-параметров согласующего устройства.параметры согласующей цепи рассчитываются по функциям входного сопротивления и сопротивления нагрузки. Элементы матрицы сопротивлений определяются следующими выражениями для варианта А:
и для варианта В:
Расчет z-параметров следует начинать с определения полинома числителя z12. При этом необходимо обратить внимание на то, что после извлечения корня полином числителя z12 может быть либо четным, либо нечетным. Четный полином указывает на вариант А z-параметров, нечетный - на вариант В. Кроме того, необходимо обеспечить наличие всех нулей Проверка ограничений. Физическая реализуемость системы z-параметров возможна в том случае, когда удовлетворяется система ограничений для заданной нагрузки и функции передачи. При расчете z-параметров в среде MathCAD программа Find содержит ограничения. Для нагрузки 1-го класса ограничение имеет вид:
Для расчета z-параметров воспользуемся вариантом B так как полином Z12 нечетный
Расчет общего знаменателя
Расчет числителя Z11: Расчет числителя Z22: Расчет числителя Z12:
Для расчета z-параметров воспользуемся вариантом B так как полином Z12 нечетный. В результате вычислений получили:
Произведем замену
Проверка расчета. Чтобы убедиться в правильности расчета, необходимо определить входное сопротивление согласующей цепи с сопротивлением нагрузки на выходе. Частотная характеристика, построенная на основании Z-параметров, должна совпадать с принятой в качестве исходной для расчета. Входное сопротивление согласующей цепи связано с Z-параметрами выражением
где d(w) - определитель матрицы Z-параметров
zl(w) - сопротивление нагрузки
Убедимся в правильности расчета используя формулу (4.17)
Рисунок 4.3 - Частотная характеристика по Z-параметрам
Частотная характеристика совпадает с исходной характеристикой, значит расчет верный.
|
||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 60; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.120.103 (0.005 с.) |


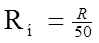 ,
, 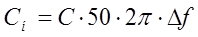 ,
, , (4.11)
, (4.11) , (4.12)
, (4.12) . В зависимости от их расположения на плоскости комплексной частоты, различают следующие классы нагрузок:
. В зависимости от их расположения на плоскости комплексной частоты, различают следующие классы нагрузок: ;
;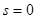 ;
; ;
; .
.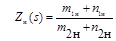 .
.
 ,
,

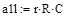
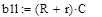
 .
. (4.14)
(4.14)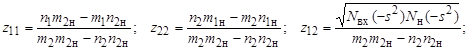 (4.15)
(4.15)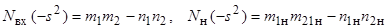 .
. в полиноме
в полиноме  не меньшей кратности. Физический смысл этого условия состоит в том, что на частотах, на которых
не меньшей кратности. Физический смысл этого условия состоит в том, что на частотах, на которых 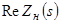 обращается в нуль, невозможна передача сигнала от источника в нагрузку при любой структуре и параметрах реактивного четырехполюсника.
обращается в нуль, невозможна передача сигнала от источника в нагрузку при любой структуре и параметрах реактивного четырехполюсника.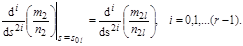

 .
. .
.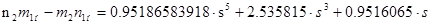 .
. .
. ;
; ;
;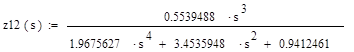 ;
; получим:
получим: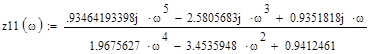 ;
; ;
;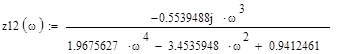 ;
;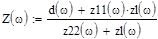 , (4.17)
, (4.17)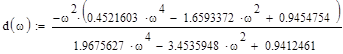 ,
, .
.