
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы теории ошибок измерений
29. Критерии точности измерений Другая задача теории ошибок (оценка точности) решается благодаря установленным в теории вероятностей критериям. В качестве критериев оценки точности используется вероятная, средняя и средняя квадратическая ошибки. Вероятная ошибка r – это ошибка в середине ряда, все ошибки которого расположены по возрастанию или убыванию их абсолютных значений. Например, имеем ряд случайных ошибок: +4,-2,-1,-3,0,+2,+1,0. Расположим ошибки ряда по возрастанию абсолютных значений: 0,0,1,1,2,2,3,4. Вероятная ошибка равна 1,5 т.е. та ошибка, которая находиться в середине ряда. Средняя ошибка вычисляется по приближенной формуле: Средняя квадратическая ошибка является более надёжным критерием оценки точности и обладает рядом достоинств: 1) крупные случайные ошибки, фактически определяющие качество измерений, окажут определяющее влияние на величину m, так как при вычислении средней квадратической ошибки случайные ошибки возводятся в квадрат. 2) даже при малом числе измерений получается достаточно надежная оценка точности. Так, если n=8 то для приведенного ряда ошибок средней квадратической ошибки 30 Средняя ошибка
31. Средняя квадратическая ошибка Точность результатов измерений оценивается средней квадратической ошибкой. Средняя квадратическая ошибка одного измерения вычисляется по формуле: 32. Вероятная ошибка Вероятная ошибка r – это ошибка в середине ряда, все ошибки которого расположены по возрастанию или убыванию их абсолютных значений. Например, имеем ряд случайных ошибок: +4,-2,-1,-3,0,+2,+1,0. Расположим ошибки ряда по возрастанию абсолютных значений: 0,0,1,1,2,2,3,4. Вероятная ошибка равна 1,5 т.е. та ошибка, которая находиться в середине ряда.
33. Предельная ошибка Предельная ошибка не должна превышать утроенной средней квадратической ошибки, т.е. ε = 3 x m. Иногда о точности измерений судят не по абсолютной величине средней квадратической или предельной погрешности, а по величине относительной ошибки.
|
||||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 317; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.131.168 (0.003 с.) |
 , где |
, где |  | - абсолютная величина случайной ошибки. Наибольшее распространение в геодезии в качестве критерия оценок точности получила средняя квадратическая ошибка, предложенная К.Ф.Гауссом. Её значение вычисляется по формуле:
| - абсолютная величина случайной ошибки. Наибольшее распространение в геодезии в качестве критерия оценок точности получила средняя квадратическая ошибка, предложенная К.Ф.Гауссом. Её значение вычисляется по формуле:  , где [
, где [ 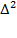 ]=
]=  для приведенного ряда имеем V=1,6 m=2,1 r=1,5.
для приведенного ряда имеем V=1,6 m=2,1 r=1,5. =0,5 не будет превышать 25% от m, что практически считается малой величиной
=0,5 не будет превышать 25% от m, что практически считается малой величиной  3) по величине m можно определить предельную ошибку:
3) по величине m можно определить предельную ошибку:  . В практике полевых работ допускается
. В практике полевых работ допускается  . При измерении линий можно применять относительную среднюю квадратическую ошибку, например
. При измерении линий можно применять относительную среднюю квадратическую ошибку, например 
 Средней ошибкой
Средней ошибкой  называют оценку среднего отклонения n1 (центрального абсолютного момента первого порядка) и вычисляют по формуле:
называют оценку среднего отклонения n1 (центрального абсолютного момента первого порядка) и вычисляют по формуле: где [v2] – сумма квадратов вероятнейших ошибок; n – число измерений. Средняя квадратическая ошибка арифметической середины вычисляется по формуле:
где [v2] – сумма квадратов вероятнейших ошибок; n – число измерений. Средняя квадратическая ошибка арифметической середины вычисляется по формуле: 



