
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В XI классе на уроки алгебры уходит по 3 часа в неделю, всего получается 102 часа в год. На изучение показательной, логарифмической и степенной функции по программе уходит 36 часов.
В программу входит рассмотрение и изучение следующих вопросов: Понятие о степени с рациональным показателем. Решение иррациональных уравнений. Показательная функция, её свойства и график. тождественные преобразования показательных выражений. Решение показательных уравнений и неравенств. Логарифм числа. Основные свойства логарифмов. Логарифмическая функция, её свойства и график. Решение логарифмических уравнений и неравенств. Производная показательной функции. Число Основной целью раздела изучения показательной и логарифмической функции является ознакомление учащихся с показательной, логарифмической и степенной функцией; научить учащихся решать показательные и логарифмические уравнения и неравенства. Понятия корня Изучение свойств показательной, логарифмической и степенной функции построено в соответствии с принятой общей схемой исследования функций. При этом обзор свойств дается в зависимости от значений параметров. Показательные и логарифмические неравенства решаются с опорой на изученные свойства функций. Характерной особенностью курса являются систематизация и обобщение знаний учащихся, закрепление и развитие умений и навыков, полученных в курсе алгебры, что осуществляется как при изучении нового материала, так и при проведении обобщающего повторения. Тождественные преобразования и вычисления Показательных и логарифмических выражений
Обобщение понятия степени. Определение: Корнем
Согласно данному определению корень Определение: Арифметическим корнем При четных При нечетных значениях Для корней нечетной степени справедливо равенство Замечание 1: Для любого действительного
Замечание 2: Удобно считать, что корень первой степени из числа Напомним известные свойства арифметических корней Для любого натурального 1. 2. 3. 4. 5. Степень с рациональным показателем. Выражение Для любых чисел
Отметим так же, что если
Определение: Степенью числа Итак, по определению При сформулированном определении степени с рациональным показателем сохраняются основные свойства степеней, верные для любых показателей (разница заключается в том, что свойства верны только для положительных оснований).
Показательная функция. Определение: Функция, заданная формулой Сформулируем основные свойства показательной функции. 1. Область определения – множество 2. Область значений – множество 3. При График функции
Рис. 1 4. При любых действительных значениях
Эти формулы называют основными свойствами степеней. Можно так же заметить, что функция
Логарифмическая функция. Определение: Логарифмом числа Формулу При работе с логарифмами применяются следующие их свойства, вытекающие из свойств показательной функции: При любом 1. 2. 3. 4. 5. Основные свойства логарифмов широко применяются в ходе преобразования выражений, содержащих логарифмы. Например, часто используется формула перехода от одного основания логарифма к другому: Пусть Определение: Функцию, заданную формулой Перечислим основные свойства логарифмической функции. 1. Область определения логарифмической функции – множество всех положительных чисел 2. Область значений логарифмической функции – множество всех действительных чисел. 3. Логарифмическая функция на всей области определения возрастает (при График функции
Рис. 2 Графики показательной и логарифмической функций, имеющих одинаковое основание, симметричны относительно прямой
Рис. 3 Глава 3. Тождественные преобразования показательных и
|
||||||
|
Последнее изменение этой страницы: 2019-10-31; просмотров: 221; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.227.69 (0.021 с.) |
 и натуральный логарифм. Производная степенной функции.
и натуральный логарифм. Производная степенной функции.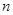 -ой степени и степени с рациональным показателем являются обобщением понятий квадратного корня и степени с целым показателем. Следует обратить внимание учащихся, что рассматриваемые здесь свойства корней и степеней с рациональным показателем аналогичны тем свойствам, которыми обладают изученные ранее квадратные корни и степени с целыми показателями. Необходимо уделить достаточно времени отработке свойств степеней и формированию навыков тождественных преобразований. Понятие степени с иррациональным показателем вводится на наглядно-интуитивной основе. Этот материал играет вспомогательную роль и используется при введении показательной функции.
-ой степени и степени с рациональным показателем являются обобщением понятий квадратного корня и степени с целым показателем. Следует обратить внимание учащихся, что рассматриваемые здесь свойства корней и степеней с рациональным показателем аналогичны тем свойствам, которыми обладают изученные ранее квадратные корни и степени с целыми показателями. Необходимо уделить достаточно времени отработке свойств степеней и формированию навыков тождественных преобразований. Понятие степени с иррациональным показателем вводится на наглядно-интуитивной основе. Этот материал играет вспомогательную роль и используется при введении показательной функции. -ой степени из чиста
-ой степени из чиста  называется такое число,
называется такое число,  -я степень которого равна
-я степень которого равна  -ой степени из числа
-ой степени из числа  – это решение уравнения
– это решение уравнения  . Число корней этого уравнения зависит от
. Число корней этого уравнения зависит от  . Как известно, на промежутке
. Как известно, на промежутке  эта функция при любом
эта функция при любом  имеет неотрицательный корень и при том только один. Его называют арифметическим корнем
имеет неотрицательный корень и при том только один. Его называют арифметическим корнем  -ой степени из числа
-ой степени из числа 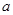 и обозначают
и обозначают  ; число
; число  называют так же радикалом.
называют так же радикалом. четна. Отсюда следует, что если
четна. Отсюда следует, что если  , то уравнение
, то уравнение 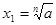 , имеет также корень
, имеет также корень  . Если
. Если  , то корень один:
, то корень один: 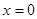 ; если
; если  , то это уравнение корней не имеет, поскольку четная степень любого числа неотрицательна.
, то это уравнение корней не имеет, поскольку четная степень любого числа неотрицательна. и, в частности, при
и, в частности, при  .
.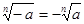 . В самом деле,
. В самом деле,  , т.е. число –
, т.е. число –  . Но такой корень при нечетном
. Но такой корень при нечетном 
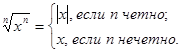
 равен
равен  . Корень второй степени из числа
. Корень второй степени из числа  -ой степени.
-ой степени. и любых неотрицательных целых чисел
и любых неотрицательных целых чисел  справедливы равенства:
справедливы равенства:



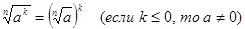 .
. определено для всех
определено для всех  . Напомним свойства таких степеней.
. Напомним свойства таких степеней.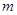 и
и 
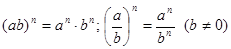

 , то
, то  при
при 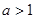 и
и  при
при  .
. , где
, где  – целое число, а
– целое число, а  , называется число
, называется число  .
. .
. (где
(где  ), называется показательной функцией с основанием
), называется показательной функцией с основанием  .
.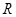 действительных чисел.
действительных чисел. всех положительных действительных чисел.
всех положительных действительных чисел. функция возрастает на всей числовой прямой; при
функция возрастает на всей числовой прямой; при  функция убывает на множестве
функция убывает на множестве  и
и  справедливы равенства
справедливы равенства 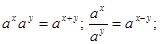


 .
. (где
(где  ,
,  ) называют основным логарифмическим тождеством.
) называют основным логарифмическим тождеством.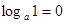



 для любого действительного
для любого действительного  .
. .
. называют логарифмической функцией с основанием
называют логарифмической функцией с основанием  .
. ) или убывает (при
) или убывает (при  ).
). (рис. 2)
(рис. 2) (рис. 3).
(рис. 3).


