
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Возведение многочлена в степеньСодержание книги Поиск на нашем сайте
КУРСОВАЯ РАБОТА по дисциплине: «Программирование» на тему: «Многочлены»
студент группы шифр ФИО «____» ______________ 201 г. _________________________ подпись студента)
Проверил ФИО Оценка _____________________ ____________________________ (подпись преподавателя) «___» ____________ 201 г.
Лысьва, 2013г.
Содержание 1. Введение.................................................................................................................................... 3 1.2 Постановка задачи............................................................................................................... 4 1.3 Основная теория.................................................................................................................. 4 2. Основная часть.......................................................................................................................... 8 2.1 Возможные исходные данные........................................................................................... 8 2.2 Неформальное изложение алгоритма................................................................................ 8 }3. Набор тестов для класса....................................................................................................... 14 3. Набор тестов для класса......................................................................................................... 15 3.1 Тесты для сложения двух многочленов.......................................................................... 15 3.2 Тесты для вычитания двух многочленов........................................................................ 17 3.3 Тесты для умножения двух многочленов....................................................................... 19 3.4 Тесты для деления двух многочленов............................................................................. 21 3.5 Тесты для нахождения остатка от деления..................................................................... 22 3.6 Тесты для операции отношения равно............................................................................ 23 3.7 Тесты для операции отношения не равно....................................................................... 25 3.8 Тесты для операции возведения многочлена в натуральную степень k.................... 26 3.9 Тесты для вычисления производной от многочлена.................................................... 28 3.10 Тесты для вычисления значения в точке x0.................................................................. 28 3.11 Тесты на вывод многочлена........................................................................................... 29 3.12 Тесты на нахождение наибольшего общего делителя двух многочленов................ 31 4. Руководство пользователя...................................................................................................... 33 5. Заключение.......................................................................................................................... 34 Список использованных источников....................................................................................... 35 Приложения................................................................................................................................. 36
Введение Изучение полиномиальных уравнений и их решений составляло едва ли не главный объект «классической алгебры». С изучением многочленов связан целый ряд преобразований в математике: введение в рассмотрение нуля, отрицательных, а затем и комплексных чисел, а также появление теории групп как раздела математики и выделение классов специальных функций в анализе. Многочлены также играют ключевую роль в алгебраической геометрии, объектом которой являются множества, определённые как решения систем многочленов. Поэтому создание легкой и доступной программы способной быстро выполнять нужные действия с многочленами любой степени является практичной и упрощает работу, избавляя нас от рутинных вычислений. Цель работы Научиться работать с классами и создать класс, в котором будет создан набор функций, подпрограмм и тп для работы с многочленами от одной переменной (первый многочлен степени m, второй — степени n), а именно выполнять операции: сложения, умножения, вычитания, деления с остатком, возведения степень, операции отношения (равно, не равно), возведение в натуральную степень, вычисление производной от многочлена, вычисление значения в точке x 0. Постановка задачи Реализовать в виде класса набор подпрограмм для выполнения операций с многочленами от одной переменной (первый многочлен степени m, второй — степени n): 1) сложение; Используя этот класс, решить задачи:
Основная теория Многочлен от n переменных — это сумма одночленов или, строго, — конечная формальная сумма вида.1
· · В частности, многочлен от одной переменной есть конечная формальная сумма вида
· ·
Привести многочлен к стандартному виду — означает привести к стандартному виду все его члены, а затем привести подобные члены. 1 Сложить два многочлена — это значит представить их сумму Чтобы решить многочлен, надо свести подобные члены. Например: Вычесть из одного многочлена другой — это значит представить их разность в стандартном виде.1 При вычитании многочленов важно помнить, что после раскрытия скобок знаки во втором многочлене меняются на противоположные. Например: Умножить многочлен на многочлен - это значит, каждый член одного многочлена умножить на каждый член другого многочлена и полученные одночлены сложить. 1 Например: Деление многочленов — алгоритм деления многочлена Пример: 1. Делим первый элемент делимого на старший элемент делителя, помещаем результат под чертой
2. Умножаем делитель на полученный выше результат деления (на первый элемент частного). Записываем результат под первыми двумя элементами делимого
3. Вычитаем полученный после умножения многочлен из делимого, записываем результат под чертой
4. Повторяем предыдущие 3 шага, используя в качестве делимого многочлен, записанный под чертой.
5. Повторяем шаг 4.
6. Конец алгоритма. Таким образом, многочлен Основная часть 2.1 Возможные исходные данные · Многочлены(коэффициенты при переменных, степени переменных), алгоритмы решения задач. · Операции над многочленами: сложение, умножение, вычитание, деление с остатком, возведение степень, операции отношения (равно, не равно), возведение в натуральную степень, вычисление производной от многочлена, вычисление значения в точке x0. Алгоритм вывода многочлена · Выводим на экран “ y =”; · Выводим на экран элемент многочлена с наибольшей степенью; · Выводим поочередно все элементы многочлена, начиная с большей степени до единицы включительно; · Если коэффициент при x равен нулю не выводим этот элемент; · Выводим свободный элемент.
void mnogochlen::vivod() {int j,i;
cout<<"y="; if(stepen==0){cout<<koof[0];} else{ if(koof[stepen]>0) { cout<<koof[stepen]<<"x^"<<stepen; }
else { if(koof[stepen]<0) {cout<<koof[stepen]<<"x^"<<stepen;} else{cout<<"";} }
j=stepen-1;
for(i=j;i>=1;i--)
{ if(koof[i]>0) { cout<<"+"<<koof[i]<<"x^"<<i;}
else { if(koof[i]<0) {cout<<koof[i]<<"x^"<<i;}
else{cout<<"";}} } if(koof[0]>0) { cout<<"+"<<koof[0]<<endl;}
else { if(koof[0]<0) {cout<<koof[i]<<endl;}
else{cout<<endl;} } } } Тесты на вывод многочлена · Случай, когда многочлен содержит только положительные элементы Введите степень многочлена (натуральное число) 3 Введите свободный элемент 2 Введите x в степени 1 9 Введите x в степени 2 7 Введите x в степени 3 3 y=3x3+7x2+9x+2 · Случай, когда многочлен содержит только отрицательные элементы Введите степень многочлена (натуральное число) 3 Введите свободный элемент -3 Введите x в степени 1 -5 Введите x в степени 2 -7 Введите x в степени 3 -2 y=-2x3-7x2-5x-3 · Случай, когда многочлен содержит коэффициенты и положительные и отрицательные Текущая кодовая страница: 1251 Введите степень многочлена (натуральное число) 4 Введите свободный элемент 2 Введите x в степени 1 -5 Введите x в степени 2 -10 Введите x в степени 3 5 Введите x в степени 4 3 y=3x4+5x3-10x2-5x+2 · Случай, когда многочлен содержит нулевые коэффициенты Введите степень многочлена (натуральное число) 4 Введите свободный элемент3 Введите x в степени 1 0 Введите x в степени 2 0 Введите x в степени 3 0 Введите x в степени 4 6 y=6x4+3 · Случай, когда в многочлене нет свободного элемента Введите степень многочлена (натуральное число)3 Введите свободный элемент0 Введите x в степени 1 4 Введите x в степени 2 -7 Введите x в степени 3 2 y=2x3-7x2+4x · Случай, когда в многочлене только свободный элемент Введите степень многочлена (натуральное число) 0 Введите свободный элемент5 y=5 Руководство пользователя Открываем программу «Многочлены» двойным щелчком мыши. Затем следуем инструкциям программы. Программа позволяет выполнять основные операции над многочленами. Многочлены представлены в стандартном виде, начиная от большей степени. «^» обозначает, какая степень у данного x. Заключение В данной курсовой работе мы, используя полученные ранее математические знания, написали работоспособную программу, которая может: складывать, вычитать, умножать, делить многочлены натуральной степени, находить значение в указанной точке, производную от многочлена, а так же настроены вывод результатов и ввод данных, который делает «общение» с пользователем более простым и понятным. Данную программу можно использовать для решения и проверки задач средней, а так же старшей школ. Приложения 1. Найти наибольший общий делитель многочленов P(x) и Q(x). #include <iostream>#include <cmath> #include <string> using namespace std; class mnogochlen { int stepen; int koof[100]; public: void sozdanie(); /* создание многочлена */ void vivod(); /* вывод многочлена */ mnogochlen operator +(mnogochlen m); /* сложение многочленов */ mnogochlen operator -(mnogochlen m); /* вычитание многочленов */ mnogochlen operator *(mnogochlen m); /* умножение многочленов */ bool operator ==(mnogochlen m); /* равны ли многочлены? */ bool operator!=(mnogochlen m); /* не равны ли многочлены? */ mnogochlen proizvodnaa(); /* нахождение производной от многочлена */ double znachenie(double x); /* нахождение значения при заданном x */ mnogochlen stepeny(int k); /*возведение многочлена в степень*/ mnogochlen operator /(mnogochlen m); /*деление многочленов */ mnogochlen operator %(mnogochlen m); /*нахождение остатка от деления*/ }; // находжение остатака от деления mnogochlen mnogochlen:: operator %(mnogochlen m){ mnogochlen c,d,g; bool a; int i,l,k; l=stepen-m.stepen; for (i=0;i<100;i++) {c.koof[i]=0; d.koof[i]=0;} while (stepen>=m.stepen){ c.stepen=stepen-m.stepen; c.koof[c.stepen]=koof[stepen]/m.koof[m.stepen]; d=m*c; * this =* this -d; } c.stepen=l; return * this;} //Деление многочленов mnogochlen mnogochlen:: operator /(mnogochlen m){ mnogochlen c,d,g; int i,l,k; l=stepen-m.stepen; for (i=0;i<100;i++) {c.koof[i]=0; d.koof[i]=0;} while (stepen>=m.stepen){ c.stepen=stepen-m.stepen; c.koof[c.stepen]=koof[stepen]/m.koof[m.stepen]; d=m*c; * this =* this -d; } c.stepen=l; return c;} /* Нахождение производной от многочлена */ mnogochlen mnogochlen::proizvodnaa(){mnogochlen c; int i, j; c.stepen=stepen; for (i=1;i<=stepen;i++) {c.koof[i-1]=koof[i]*i;}c.stepen--; return c; } /* Равны ли многочлены? */ bool mnogochlen:: operator ==(mnogochlen m){ bool priznak; int i; if (stepen!=m.stepen){priznak=0;} else { for (i=0;i<=stepen;i++) { if (koof[i]!=m.koof[i]) {priznak=0; break;} else {priznak=1;} } } return priznak; } /* не равны ли многочлены? */ bool mnogochlen:: operator!=(mnogochlen m){ bool priznak; int i; if (stepen!=m.stepen){priznak=0;} else { for (i=0;i<=stepen;i++) { if (koof[i]!=m.koof[i]) {priznak=1; break;} else {priznak=0;} } } return priznak; } /* умножение многочленов */ mnogochlen mnogochlen:: operator *(mnogochlen m) {mnogochlen d; int i,j,k; k=stepen+m.stepen; for (i=0;i<=k;i++) { d.koof[i]=0; } for (i=0;i<=stepen;i++) { for (j=0;j<=m.stepen;j++) { d.koof[i+j]+=koof[i]*m.koof[j]; } } d.stepen=m.stepen+stepen; return d; } /* разность многочленов */ mnogochlen mnogochlen:: operator -(mnogochlen m){mnogochlen d; int i,max; if (stepen>m.stepen) max=stepen; else max=m.stepen; if (stepen>m.stepen) { for (i=m.stepen+1;i<=max;i++) m.koof[i]=0;} else { for (i=stepen+1;i<=max;i++) koof[i]=0; } for (i=0;i<=max;i++) { d.koof[i]=koof[i]-m.koof[i]; } d.stepen=max; for (i=max;i>0;i--) { if (d.koof[i]==0){d.stepen--;} else { break;}} return d;} /* нахождение значения многочлена */ double mnogochlen::znachenie(double x){ double y; int i; y=koof[0]; for (i=1;i<=stepen;i++) {y+=pow(x,i)*koof[i];} return y;} /* сложение многочленов */ mnogochlen mnogochlen:: operator +(mnogochlen m){mnogochlen d; int i,max; if (stepen>m.stepen) max=stepen; else max=m.stepen; if (stepen>m.stepen){ for (i=m.stepen+1;i<=max;i++) m.koof[i]=0;} else { for (i=stepen+1;i<=max;i++) koof[i]=0; } for (i=0;i<=max;i++) { d.koof[i]=koof[i]+m.koof[i]; } d.stepen=max; for (i=max;i>0;i--) { if (d.koof[i]==0){d.stepen--;} else { break;}} return d; return d;} /* Создание многочлена */ void mnogochlen::sozdanie(){ int i; cout<<”Введите степень многочлена (натуралное число)"<<endl; cin>>stepen; cout<<"Введите свободный элемент"<<endl; cin>>koof[0]; for (i=1;i<=stepen;i++) { cout<<"Введите x в степени "<<i<<" "; cin>>koof[i]; }} /* вывод многочлена */ void mnogochlen::vivod(){ int j,i; cout<<"y="; if (stepen==0){cout<<koof[0];} else { if (koof[stepen]>0) { cout<<koof[stepen]<<"x^"<<stepen; } else { if (koof[stepen]<0) {cout<<koof[stepen]<<"x^"<<stepen;} else {cout<<"";} } j=stepen-1; for (i=j;i>=1;i--) { if (koof[i]>0) { cout<<"+"<<koof[i]<<"x^"<<i;} else { if (koof[i]<0) {cout<<koof[i]<<"x^"<<i;} else {cout<<"";}} } if (koof[0]>0) { cout<<"+"<<koof[0]<<endl;} else { if (koof[0]<0) {cout<<koof[i]<<endl;} else {cout<<endl;} }}} /* возведение многочлена в степень */ mnogochlen mnogochlen::stepeny(int k){ int i; mnogochlen d,c; c.stepen=stepen; for (i=0;i<=stepen;i++) {c.koof[i]=koof[i];} d.stepen=0; d.koof[0]=1; for (i=1;i<=k;i++) {d=d*c; } return d;} int main() { mnogochlen P,Q,c; double s,r; system("chcp 1251"); cout<<"Введите первый многочлен”<<endl; P.sozdanie(); P.vivod(); cout<<"Введите второй многочлен"<<endl; Q.sozdanie(); Q.vivod(); cout<<"Введите степень, в которую следует возвести первый многочлен"<<endl; cin>>s; P=P.stepeny(s); cout<<" Введите степень, в которую следует возвести второй многочлен "<<endl; cin>>r; Q=Q.stepeny(r); cout<<"Результат операций P^s-Q^r"<<endl; c=P-Q; c.vivod(); system ("PAUSE"); return 0; }2. На КУРСОВАЯ РАБОТА по дисциплине: «Программирование» на тему: «Многочлены»
студент группы шифр ФИО «____» ______________ 201 г. _________________________ подпись студента)
Проверил ФИО Оценка _____________________ ____________________________ (подпись преподавателя) «___» ____________ 201 г.
Лысьва, 2013г.
Содержание 1. Введение.................................................................................................................................... 3 1.2 Постановка задачи............................................................................................................... 4 1.3 Основная теория.................................................................................................................. 4 2. Основная часть.......................................................................................................................... 8 2.1 Возможные исходные данные........................................................................................... 8 2.2 Неформальное изложение алгоритма................................................................................ 8 }3. Набор тестов для класса....................................................................................................... 14 3. Набор тестов для класса......................................................................................................... 15 3.1 Тесты для сложения двух многочленов.......................................................................... 15 3.2 Тесты для вычитания двух многочленов........................................................................ 17 3.3 Тесты для умножения двух многочленов....................................................................... 19 3.4 Тесты для деления двух многочленов............................................................................. 21 3.5 Тесты для нахождения остатка от деления..................................................................... 22 3.6 Тесты для операции отношения равно............................................................................ 23 3.7 Тесты для операции отношения не равно....................................................................... 25 3.8 Тесты для операции возведения многочлена в натуральную степень k.................... 26 3.9 Тесты для вычисления производной от многочлена.................................................... 28 3.10 Тесты для вычисления значения в точке x0.................................................................. 28 3.11 Тесты на вывод многочлена........................................................................................... 29 3.12 Тесты на нахождение наибольшего общего делителя двух многочленов................ 31 4. Руководство пользователя...................................................................................................... 33 5. Заключение.......................................................................................................................... 34 Список использованных источников....................................................................................... 35 Приложения................................................................................................................................. 36
Введение Изучение полиномиальных уравнений и их решений составляло едва ли не главный объект «классической алгебры». С изучением многочленов связан целый ряд преобразований в математике: введение в рассмотрение нуля, отрицательных, а затем и комплексных чисел, а также появление теории групп как раздела математики и выделение классов специальных функций в анализе. Многочлены также играют ключевую роль в алгебраической геометрии, объектом которой являются множества, определённые как решения систем многочленов. Поэтому создание легкой и доступной программы способной быстро выполнять нужные действия с многочленами любой степени является практичной и упрощает работу, избавляя нас от рутинных вычислений. Цель работы Научиться работать с классами и создать класс, в котором будет создан набор функций, подпрограмм и тп для работы с многочленами от одной переменной (первый многочлен степени m, второй — степени n), а именно выполнять операции: сложения, умножения, вычитания, деления с остатком, возведения степень, операции отношения (равно, не равно), возведение в натуральную степень, вычисление производной от многочлена, вычисление значения в точке x 0. Постановка задачи Реализовать в виде класса набор подпрограмм для выполнения операций с многочленами от одной переменной (первый многочлен степени m, второй — степени n): 1) сложение; Используя этот класс, решить задачи:
Основная теория Многочлен от n переменных — это сумма одночленов или, строго, — конечная формальная сумма вида.1
· · В частности, многочлен от одной переменной есть конечная формальная сумма вида
· ·
Привести многочлен к стандартному виду — означает привести к стандартному виду все его члены, а затем привести подобные члены. 1 Сложить два многочлена — это значит представить их сумму Чтобы решить многочлен, надо свести подобные члены. Например: Вычесть из одного многочлена другой — это значит представить их разность в стандартном виде.1 При вычитании многочленов важно помнить, что после раскрытия скобок знаки во втором многочлене меняются на противоположные. Например: Умножить многочлен на многочлен - это значит, каждый член одного многочлена умножить на каждый член другого многочлена и полученные одночлены сложить. 1 Например: Деление многочленов — алгоритм деления многочлена Пример: 1. Делим первый элемент делимого на старший элемент делителя, помещаем результат под чертой
2. Умножаем делитель на полученный выше результат деления (на первый элемент частного). Записываем результат под первыми двумя элементами делимого
3. Вычитаем полученный после умножения многочлен из делимого, записываем результат под чертой
4. Повторяем предыдущие 3 шага, используя в качестве делимого многочлен, записанный под чертой.
5. Повторяем шаг 4.
6. Конец алгоритма. Таким образом, многочлен Возведение многочлена в степень Чтобы возвести двучлен в четвертую, пятую и т.д. степень, надо последовательно умножить разложенный многочлен на самого себя несколько раз. Например: p 1(x)= (3 x 2 – 2)3=(3 x 2 – 2) (3 x 2 – 2) (3 x 2 – 2)= (3 x 2 – 2)(9 x 2 – 12 x +4)= 27 x 3+54 x2+ 36 x +8. Два многочлена p 1(x) и p 2(x) считаются равными, если равны их коэффициенты при одинаковых степенях переменной х и свободные члены (равны их соответствующие коэффициенты). В этом случае пишут: p 1 (x) = p 2 (x).3 Производная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке).2 Для вычисления производной от многочлена нам потребуются знания таблицы производных: Например: Класс — разновидность абстрактного типа данных в объектно-ориентированном программировании, характеризуемый способом своего построения. Наряду с понятием «объекта» класс является ключевым понятием в ООП. Суть отличия классов от других абстрактных типов данных состоит в том, что при задании типа данных класс определяет одновременно и интерфейс, и реализацию для всех своих экземпляров, а вызов метода-конструктора обязателен. 3 На практике объектно-ориентированное программирование св
|
||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 411; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.152.168 (0.009 с.) |

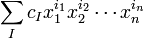 , где
, где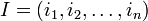 — набор из целых неотрицательных чисел, именуемый мультииндексом,
— набор из целых неотрицательных чисел, именуемый мультииндексом,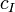 — число, именуемое коэффициент многочлена, зависящее только от мультииндекса I.
— число, именуемое коэффициент многочлена, зависящее только от мультииндекса I. , где
, где — фиксированные коэффициенты,
— фиксированные коэффициенты,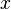 — переменная.
— переменная.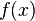 на многочлен
на многочлен 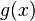 , степень которого меньше или равна степени многочлена
, степень которого меньше или равна степени многочлена  .
.
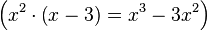 .
.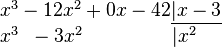
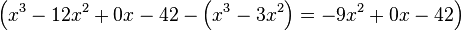 .
.

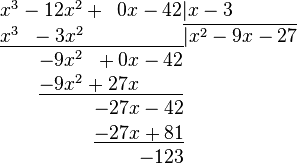
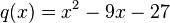 — частное деления, а
— частное деления, а 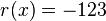 — остаток.
— остаток.


