
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Стратегии управления многономенклатурными запасамиСодержание книги
Поиск на нашем сайте
Запасы, управление запасами и стратегии оптимального управления ими - на сегодняшний день эти понятия являются атрибутами многих систем логистики. Желание повысить эффективность работы подобных систем ещё до бурного развития логистики, которое мы наблюдаем в последнее десятилетие, привело к созданию специальных научных направлений, например, теории массового обслуживания. Наряду с развитием теории массового обслуживания, основное предназначение которой - обеспечить эффективную организацию работы систем, описываемых соответствующими моделями обслуживания, пристальное внимание уделялось и уделяется в настоящее время другим близким научным направлениям, а именно: изучению специального класса моделей, которые непосредственно при анализе систем массового обслуживания не рассматриваются, но существенно влияют на показатели эффективности работы системы в целом. Это модели теории управления запасами. Например, если обслуживание (в модели соответствующей системы массового обслуживания) предполагает расход некоторого продукта либо товара, то в рамках самой такой модели обычно неявно предполагается, что этот продукт или товар всегда имеется в достаточном количестве [14, с. 63]. В реальных моделях требуется решать вопросы организации запаса и пополнения соответствующего продукта/товара, в частности, это выбор моментов подачи заказов на пополнение запаса; выбор объёма партии заказа для пополнения запаса. Соответствующие модели задач называют моделями управления запасами [3, с. 14-15]. Среди них выделяют однокомпонентные (однономенклатурные) модели, в которых рассматривается только один вид товара или продукта. Альтернативой им являются соответственно многокомпонентные (многономенклатурные) модели [3, с. 16]. Деятельность производственных предприятий автомобильной отрасли сопряжена с решением многих логистических задач, одной из которых является задача управления широким ассортиментом запасных частей и комплектующих к автомобилям. Сложность данной проблемы трудно переоценить, потому что по подсчётам аналитиков на разных уровнях систем снабжения номенклатура запасов автозапчастей варьируется от 30-50 до 500-700 тысяч наименований [8, с. 24]. Для решения вопросов стратегического управления таким обширным ассортиментом традиционно используется АВС классификация, помогающая определить области номенклатурных групп, к которым применимы общие принципы управления. Но в любом случае даже выделение более узких диапазонов ассортиментного перечня подразумевает работу с порядка 1,5-2 тысячами наименований категории А (самой малой области), что создаёт трудности в решении таких логистических задач, как расчёт оптимальной партии поставки. Рассмотрим, какими методами может решаться вышеупомянутая задача [9, с. 60]. Всем известна формула Харрисона-Уилсона для расчёта оптимального периода пополнения запаса (1.1) при детерминированном спросе (и ряде прочих ограничений). Как один из вариантов оптимизации можно выполнять расчёты по каждой позиции отдельно [1, с. 91].
где Si - спрос на продукт или товар; C0 - затраты на выполнение заказа общие; Сi - затраты на выполнение заказа индивидуальные; Сhi - затраты на хранение. При этом общие издержки будут определяться как:
Для многономенклатурного запаса в учебной литературе предлагается модификация формулы Уилсона (1.3), которая подразумевает общий период поставок для всех номенклатур и экономию за счёт транзакционных издержек при увеличении затрат на хранение.
где τi* - периодичность поставки; При этом суммарные затраты будут равны:
Данный подход даёт существенную экономию по сравнению с однономенклатурным заказом, и в этом - её преимущество, к тому же значительно упрощаются расчёты [2, с. 85]. Таким образом, можно сделать вывод о том, что в логистической практике наиболее часто пользуются моделями пополнения запасов, построенными на основе экономичного размера заказа, определяемого по формуле Харрисона-Уилсона, и различными её модификациями, снимающими те или иные ограничения.
|
||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 302; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

 , (1.1)
, (1.1)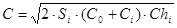 , (1.2)
, (1.2) , (1.3)
, (1.3) , (1.4)
, (1.4)


