
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многокритериальный выбор альтернатив с использованием правила нечеткого выводаСодержание книги
Поиск на нашем сайте
Рассмотрим метод многокритериального выбора альтернатив на основе композиционного правила агрегирования описаний альтернатив с информацией о предпочтениях лица, принимающего решение, которые заданы в виде нечетких суждений [2]. Сущность метода, на основе которого реализована компьютерная система, заключается в следующем. Пусть U - множество элементов, А - его нечеткое подмножество, степень принадлежности элементов к которому есть число из единичного интервала [0, 1]. Подмножества Aj являются значениями лингвистической переменной X. Допустим, что множество решений характеризуется набором критериев x1, x2,..., xp, т.е. лингвистических переменных, заданных на базовых множествах u 1, u 2,.... u p соответственно. Например, переменная x1 "качество управления" может иметь значение НИЗКОЕ, а переменная x2 "стоимость" - значение ХОРОШЕЕ и т. д. Набор из нескольких критериев с соответствующими значениями характеризует представления лица, принимающего решение, об удовлетворительности альтернативы. Переменная S "удовлетворительность" также является лингвистической. Ниже приведен пример высказывания: d1: "Если x1 = НИЗКОЕ и x2 = ХОРОШЕЕ, то S = ВЫСОКАЯ". В общем случае высказывание d1 имеет вид: d1: "Если x1 = A1, и x2 = A2i и... хр = Api то S = Bi". (4.1) Обозначим пересечение (x1 = A1i
Здесь V= U1 x U2 x... Up; v = (u 1, u 2..., u p); μAij (u j) - значение принадлежности элемента и, нечеткому множеству Aij. Тогда высказывание (4.1) можно записать в виде:
Для придания общности суждениям обозначим базовые множества U и V через W. Тогда Ai - нечеткое подмножество W, в то время как Bi - нечеткое подмножество единичного интервала I. Для представления правил используется операция импликации, для которой предложены различные способы нечеткой реализации [4]. Нечеткая импликация Лукасевича имеет вид:
где Н - нечеткое подмножество на W x I, w Аналогичным образом высказывания d1, d2,..., dq преобразуются в множества Н1, Н2,..., Нq. Их пересечением является множество D: D = H1 и для каждого (w, i)
Удовлетворительность альтернативы, которая описывается нечетким подмножеством А из W, определяется на основе композиционного правила вывода: G = Аº D, где G - нечеткое подмножество интервала I. Тогда
Сопоставление альтернатив происходит на основе точечных оценок. Для нечеткого множества С Сα = {i | μc(i) ≥ α Для каждого Сα можно вычислить среднее число элементов - М(Сα): для множества из n элементов
для Сα ={a ≤ i ≤ b}
при 0 ≤ a1 ≤ b1 ≤ a2 ≤ b2 ≤... ≤ an ≤ bn ≤ 1. Тогда точечное значение для множества С можно записать в виде:
где αmax - максимальное значение в множестве С. При выборе альтернатив для каждой из них находится удовлетворительность и вычисляется соответствующая точечная оценка. Лучшей считается альтернатива с наибольшим ее значением.
|
||||
|
Последнее изменение этой страницы: 2019-12-25; просмотров: 240; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.143.118 (0.008 с.) |

 x2 = A2i
x2 = A2i 

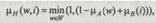
 W, i
W, i 

 I определяем α-уровневое множество (α
I определяем α-уровневое множество (α 







