
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
An overview of gradient descent optimization algorithmsСодержание книги
Поиск на нашем сайте
An overview of gradient descent optimization algorithms source: http://ruder.io/optimizing-gradient-descent/ review paper: https://arxiv.org/pdf/1609.04747.pdf slides: https://www.slideshare.net/SebastianRuder/optimization-for-deep-learning discussion: https://news.ycombinator.com/item?id=11943685 Обзор алгоритмов оптимизации Градиентного Спуска Оглавление Обзор алгоритмов оптимизации Градиентного Спуска. 1 Градиентный спуск. 2 Варианты градиентного спуска. 2 Пакетный градиентный спуск. 2 Стохастический градиентный спуск. 3 Мини-пакетный градиентный спуск. 4 Вызовы для преодоления. 4 Алгоритмы оптимизации градиентного спуска. 5 Имупльс (momentum) 5 Ускоренный градиент Нестерова. 5 Adagrad. 6 Adadelta. 7 RMSprop. 8 Adam.. 8 AdaMax. 9 Nadam.. 9 AMSGrad. 10 Визуализация алгоритмов. 11 Какой оптимизатор использовать?. 12 Распараллеливание и распределение по вычислителям SGD.. 12 Hogwild (экстремально увлечённый, вышедший из под контроля) 13 Downpour SGD (ливень/поток) 13 Ускойчевый к задержке алгоритм SGD (delay-tolerant) 13 TensorFlow.. 13 Эластичное усреднение SGD.. 13 Дополнительные стратегии для оптимизации SGD.. 13 Перемешивание и учебный план обучения. 13 Пакетная нормализация. 14 Ранняя остановка. 14 Градиент шума. 14 Заключение. 14
Градиентный спуск Градиентный спуск – один из самых популярных алгоритмов оптимизации и, безусловно, самый распространенный способ оптимизации нейронных сетей. В то же время каждая современная библиотека глубокого обучения содержит реализации различных алгоритмов градиентного спуска (например, lasagne, caffe и keras). Эти алгоритмы-оптимизаторы часто используются как «чёрный ящик», т.к. трудно найти практическое объяснение их сильных и слабых сторон. Цель этой статьи – дать представление о поведении различных алгоритмов оптимизации градиентным спуском, что поможет в их использовании. Сначала рассмотрим различные варианты градиентного спуска. Затем кратко изложим проблемы, возникающие во время обучения. Впоследствии представим наиболее распространенные алгоритмы оптимизации, рассматривая мотивацию их выбора для решения задач, и как именно происходит вывод их правил обновления. Мы также кратко рассмотрим алгоритмы и архитектуры для оптимизации градиентного спуска в параллельных и распределенных реализациях. Наконец, покажем дополнительные стратегии, которые полезны для оптимизации градиентным спуском.
Градиентный спуск – это способ минимизировать целевую функцию J(θ) модели, параметризованную θ ∈ Rd, путём обновления параметров в обратном направлении к градиенту целевой функции ∇ θ J(θ). Скорость обучения η (learning rate) определяет размер шагов, которые нужно предпринять для достижения (локального) минимума. Другими словами, следуем направлению наклона поверхности, созданной целевой функцией вниз, пока не достигнем долины. Если вы не знакомы с градиентным спуском, можете найти хорошее введение в оптимизацию нейронных сетей. Варианты градиентного спуска Существует 3 варианта градиентного спуска, которые отличаются тем, сколько данных используется для вычисления градиента целевой функции. В зависимости от объёма данных выбираем компромисс между точностью и временем выполнения обновления параметров. Пакетный градиентный спуск Старый добрый градиентный спуск, известный как пакетный градиентный спуск, вычисляет градиент функции стоимости (cost function) относительно параметров θ для всего обучающего массива данных (dataset): θ =θ − η ⋅∇ θ J(θ) Поскольку нужно рассчитать градиенты для всего набора данных, чтобы выполнить только 1 обновление, пакетный градиентный спуск может быть очень медленным и трудноразрешимым для наборов данных, которые не помещаются в памяти. Пакетный градиентный спуск также не позволяет обновлять модель онлайн, т.е. новыми примерами на лету.
Для заранее определённого числа эпох сначала вычисляем вектор градиента params_grad функции потерь (loss function) для всего массива данных относительно вектора параметров params. Отметьте, что современные библиотеки глубокого обучения обеспечивают автоматическое дифференцирование, которое эффективно вычисляет градиент по нескольким параметрам. Если вы вычисляете градиенты самостоятельно, тогда проверка градиентов – это необходимость (см. здесь несколько полезных советов о том, как правильно проверять градиенты). Затем обновляем параметры в направлении, противоположном градиентам, со скоростью обучения, определяющей насколько велико это обновление. Пакетный градиентный спуск гарантированно сходится к глобальному минимуму для выпуклых поверхностей ошибок и к локальному минимуму для невыпуклых поверхностей.
Вызовы для преодоления Старый добрый мини-пакетный градиентный спуск не гарантирует хорошей сходимости, но предлагает несколько задач, которые необходимо решить: • Сложный выбор правильной скорости обучения: слишком малая скорость обучения приводит к очень медленной сходимости, а чересчур высокая скорость обучения может препятствовать сходимости и вызывать колебания функции потерь около минимума, даже отклонение от него. • Расписания (schedules) [1] скорости обучения пытаются скорректировать скорость обучения во время обучения, например, отжиг (annealing), т.е. уменьшение скорости обучения в соответствии с заранее определённым расписанием, или падение её ниже порогового значения при изменении цели между эпохами. Эти расписания и пороги, однако, должны быть определены заранее и поэтому не могут адаптироваться к характеристикам массива данных [2]. • Кроме того, одинаковая скорость обучения применяется ко всем обновлениям параметров. Если данные редки (разряжены) и признаки имеют различные частоты появления, может быть нежелательно обновлять все из них за одинаковые промежутки, а выполнять более масштабное обновление для редко встречающихся признаков. • При минимизации распространённых для нейросетей сильно-невыпуклых функций ошибок важно избежать попадания в их многочисленные субоптимальные локальные минимумы. Dauphin et al.[3] утверждают, что сложность возникает не из-за локальных минимумов, а из-за седловых точек (saddle points), т.е. где 1 изменение имеет наклон (slope) вверх, а другое – вниз. Эти седловые точки обычно окружены плато одинаковой ошибки, что, известно, делает выход из него трудным для SGD, т.к. градиент близок к 0 во всех измерениях.
Импульс SGD испытывает затруднения при навигации по ущельям (ravines), т.е. в тех областях, где поверхность изгибается гораздо более круто в одном измерении, чем в другом [4], что характерно для локальных оптимумов. В этих сценариях SGD колеблется поперёк наклона ущелья, т.е. запинающееся (hesitant) продвижение вдоль дна к локальному оптимуму, как на рис.2.
Импульс (momentum) [5] – это метод, который помогает ускорить SGD в соответствующем направлении и подавить (dampens) колебания, как видно на рис.3. В выражение для обновления к величине обновления предыдущего шага добавляется множитель γ: v t = γ v t–1 + η ∇ θ J(θ) (найдём скорость) θ = θ – v t. (найдём следующую позицию) Примечание: некоторые реализации меняют знаки в уравнениях. Коэффициент импульса γ обычно устанавливается равным 0.9 или аналогичным значением. По сути, при использовании импульса - толкая шар вниз по склону, он накапливает импульс и становится всё быстрее и быстрее по пути (пока не достигает своей конечной скорости, если существует сопротивление воздуха, т.е. γ<1). То же самое происходит с обновлениями параметров: коэффициент импульса увеличивается для направлений, градиенты которых указывают в одну сторону, и уменьшается, где градиенты меняют свои направления. В результате получаем более быструю сходимость и уменьшение колебаний.
Adagrad Adagrad [9] – это алгоритм оптимизации на основе градиента, который делает именно это: он а даптирует скорость обучения по параметрам, выполняя небольшие обновления(т.е. низкая скорость обучения) для параметров, связанных с часто встречающимися признаками, и более крупные обновления (т.е. высокая скорость обучения) для параметров, связанных с редкими признаками. По этой причине он хорошо подходит для работы с разрежёнными данными.
Dean et al. [10] обнаружили, что Adagrad улучшил надёжность/устойчивость SGD значительно, и использовали его для обучения крупномасштабных нейронных сетей в Google, которые среди прочего научились распознавать кошек в видео на Youtube. Более того, Pennington et al. [11] использовали Adagrad для обучения встраивания слов (word embedding) GloVe, т.к. редкие слова требуют гораздо больших величин обновления, чем часто встречающиеся. Ранее мы выполняли обновление всех параметров θ одновременно, поскольку каждый параметр θi использовал одинаковую скорость обучения η. Поскольку Adagrad может использовать различную скорость обучения для каждого параметра θi на каждом шаге t, то вначале покажем Adagrad- обновление каждого параметра, затем его векторизуем. Для краткости используем gt для обозначения градиента на шаге времени t. gt, i = ∇θ J(θ t, i) Обновление SGD для каждого параметра θi на каждом шаге t становится: θ t +1, i = θ t , i – η ⋅ gt , i В правиле обновления Adagrad изменяет общую скорость обучения η на каждом шаге t для каждого параметра θi на основе прошлых градиентов, которые были вычислены для θi:
здесь Gt ∈ Rd × d – диагональная матрица, где каждый диагональный элемент i,i является суммой квадратов градиентов относительно θ i до временного шага t [12], а ϵ является сглаживающим слагаемым, которое позволяет избежать деления на 0 (обычно порядка 10−8). Интересно, что без операции квадратного корня алгоритм работает намного хуже. Поскольку Gt содержит сумму квадратов прошлых градиентов по всем параметрам θ вдоль своей диагонали, можно векторизовать реализацию, выполнив произведение ⊙ матрицы Gt на вектор gt:
Одним из главных преимуществ Adagrad является то, что он устраняет необходимость ручной настройки скорости обучения. Большинство реализаций используют значение по умолчанию 0.01 и оставляют его таким. Главная слабость Adagrad – это накопление квадратов градиентов в знаменателе: поскольку каждый добавленный член является положительным, накопленная сумма продолжает расти в процессе обучения. Что, в свою очередь, приводит к уменьшению скорости обучения, которая в конечном итоге становится бесконечно малой, в этот момент алгоритм больше не может получать дополнительные знания.
Следующие алгоритмы направлены на устранение этого недостатка.
Adadelta Алгоритм Adadelta [13] является продолжением Adagrad, который стремится сократить агрессивное монотонное уменьшение скорости обучения. Вместо того, чтобы накапливать все квадраты градиентов прошлого, Adadelta ограничивает окно накопления градиентов прошлого некоторым фиксированным размером w. Вместо неэффективного хранения w штук предыдущих квадратов градиентов, сумма рекурсивно определяется как затухающее среднее (decaying average) всех прошлых квадратов градиентов. Скользящее среднее E[g2]t (running average) на шаге времени t зависит (аналогично, как множитель γ для коэффициента импульса) только от предыдущего среднего и текущего градиента: E[g2]t = γ E[g2]t–1 + (1- γ) gt2 Устанавливаем значение γ, аналогичное коэффициенту импульса, около 0.9. Для ясности, теперь перепишем известное SGD -обновление в терминах обновления вектора параметров Δθt: Δθ t = – η ⋅ gt,i θ t+1 = θ t + Δθ t Тогда Adagrad -обновление параметров, полученное ранее, имеет вид:
Теперь можно заменить диагональную матрицу Gt на затухающее среднее E[g2]t нескольких последних квадратов градиентов:
Поскольку знаменатель – это просто критерий среднеквадратичной ошибки (RMS) градиента, можно заменить критерий его обозначением: Δθ t = –η / (RMS [ g ] t) ⊙ gt Отметим, что единицы измерения в этом обновлении (как и в SGD, импульсе или Adagrad) не совпадают, т.е. обновление должно иметь те же гипотетические единицы, что и параметр. Чтобы реализовать это, сначала нужно определить другое экспоненциально затухающее среднее, на этот раз не квадратов градиентов, а квадратов обновлений параметров: Е[Δθ2] t = γ Е[Δθ2] t –1 + (1–γ) Δθt2 Среднеквадратическая ошибка обновления параметров таким образом:
Поскольку RMS[Δθ]t неизвестна, приближаемся к ней через RMS обновления параметров до предыдущего временного шага. Замена скорости обучения η в предыдущем правиле обновления на RMS[Δθ]t−1, наконец, даёт правило обновления Adadelta:
θ t +1 = θ t + Δθt Используя Adadelta, даже не нужно устанавливать скорость обучения по умолчанию, т.к. она была исключена из правила обновления.
RMSprop RMSprop – это неопубликованный метод адаптивной скорости обучения, предложенный Geoff Hinton на 6й лекции его курса на Coursera. RMSprop и Adadelta разработаны независимо друг от друга в одно и то же время, связаны необходимостью разрешения уменьшающейся скорости обучения по порядку квадратного корня, взятого у Adagrad. RMSprop фактически идентичен 1му вектору обновления Adadelta, который был получен выше:
RMSprop также делит скорость обучения на экспоненциально затухающее среднее квадратов градиентов. Hinton предлагает установить γ равным 0.9, тогда как хорошее значение по умолчанию для скорости обучения η составляет 0.001.
Adam Адаптивная Оценка Импульсов (Adam – Adaptive Moment) [14] – это ещё 1 метод, который вычисляет адаптивные скорости обучения для каждого параметра. В дополнение к хранению экспоненциально затухающего среднего последних квадратов градиентов v t, как Adadelta и RMSprop, Adam также сохраняет экспоненциально затухающее среднее последних градиентов mt, аналогично импульсу. В то время как импульс можно рассматривать как шар, бегущий по склону, Adam ведет себя как тяжелый шар с трением, который, таким образом, предпочитает плоские минимумы на поверхности ошибки [15]. Мы вычисляем средние значения затухания прошлых и прошлых квадратов градиентов mtmt и vtvt соответственно следующим образом:
mt = β1 mt–1 + (1–β1) gt (затухающее среднее градиентов) v t = β2 v t–1 + (1–β2) g t 2 (затухающее среднее квадратов градиентов) mt и v t являются оценками первого статического момента (среднего значения – m ean) и второго момента инерции (нецентрированной дисперсии – uncentered v ariance) градиентов соответственно, отсюда и название метода. Поскольку mt и v t инициализируются как векторы нулей, авторы Adam отмечают, что они смещены к 0, особенно на начальных шагах, и особенно, когда скорости затухания (decay rates) малы (т.е. β1 и β2 близки к 1). Авторы противодействуют этим отклонениям, вычисляя скорректированные смещением оценки первого и второго моментов:
Затем эти оценки используются для обновления параметров, как в Adadelta и RMSprop, что приводит к правилу обновления Adam:
Предлагаются значения по умолчанию: β1=0.9, β2=0.999 и ϵ=10-8. Авторы эмпирически показывают, что Adam хорошо работает на практике и выгодно отличается от других методов адаптивного обучения.
AdaMax Коэффициент v t в правиле обновления Adam масштабирует градиент обратно пропорционально L 2 норме прошлых градиентов (исп. v t−1) и текущему градиенту |gt|2: v t = β2 v t−1 + (1–β2) |gt|2 Можно обобщить это обновление до нормы L p. Отметьте, что Kingma and Ba также параметризуют и β2, как β2 p: v t = β2 p v t–1 + (1- β2 p) |gt| p Нормы для больших значений p обычно становятся численно нестабильными, поэтому нормы L 1 и L 2 наиболее распространены на практике. Однако норма L ∞ также обычно демонстрирует устойчивое поведение. По этой причине авторы предлагают AdaMax (Kingma and va, 2015) и показывают, что v t с L ∞ сходится к следующему более стабильному значению. Чтобы избежать путаницы с Adam, используем ut для обозначения v t, ограниченного нормой бесконечности: ut = β2∞ v t–1 + (1–β2∞) |gt|∞ = max(β2 v t–1, |gt|) Теперь можно вставить это в уравнение обновления Adam, заменив
Обратите внимание, поскольку ut полагает операцию max, он не так подвержен к смещению в сторону 0, как mt и v t в Adam, поэтому не нужно вычислять поправку смещения для ut. Хорошими значениями по умолчанию являются η=0.002, β1=0.9 и β2=0.999.
Nadam Ранее указано, что A dam можно рассматривать как комбинацию RMSprop и импульса: RMSprop вносит экспоненциально затухающее среднее прошлых квадратов градиентов v t, в то время как импульс учитывает экспоненциально убывающее среднее прошлых градиентов mt. Ускоренный градиент Нестерова (NAG) превосходит обыкновенный метод импульса. Nadam (Nesterov-accelerated Adaptive Moment Estimation – Адаптивная Оценка Импульсов, ускоренная по Нестерову) [16], таким образом, объединяет A dam и NAG. Чтобы включить NAG в A dam, нужно изменить его коэффициент импульса mt. Давайте вспомним правило обновления импульса, используя текущую запись:
где J – целевая функция, γ – коэффициент затухания импульса, а η – размер шага. Разложение 3го уравнения выше даёт: θt +1 = θt – (γ mt –1 + η gt) Что ещё раз демонстрирует, что импульс включает в себя шаг в направлении предыдущего вектора импульса и шаг в направлении текущего градиента. Затем NAG позволяет выполнять более точный шаг в направлении градиента, обновляя параметры с шагом импульса перед вычислением градиента. Таким образом, нужно только изменить градиент gt, чтобы получить NAG:
Dozat предлагает изменить NAG следующим образом: вместо того, чтобы дважды применять шаг импульса – 1 раз для обновления градиента gt и 2й раз для обновления параметров θt +1 – теперь напрямую применяем опережающий импульс обновить текущие параметры:
Отметьте, что вместо предыдущего импульса mt −1, как в уравнении расширенногоправила обновления импульса выше, теперь используется текущий импульс mt, для того чтобы заглянуть в будущее. Таким образом, чтобы добавить импульс Нестерова к A da m, можно аналогичным образом заменить предыдущий импульс текущим импульсом. Напомним, что правило обновления A da m следующее (обратите внимание, что изменять
Расширение 2го уравнения с определениями
Обратите внимание, что
есть просто уточнённая-по-смещению (bias-corrected) оценка вектора импульса предыдущего шага времени. Таким образом, можно заменить её на
То, что знаменатель равен 1– β 1 t, а не 1– β 1 t -1, игнорируется для простоты, т.к. всё равно знаменатель будет заменён на следующем шаге. Это уравнение снова выглядит очень похоже на расширенное правило обновления импульса выше. Теперь можно добавить импульс Нестерова, как было сделано ранее, просто заменив эту уточнённую-по-смещению оценку импульса предыдущего временного шага
AMSGrad Поскольку адаптивные методы обучения стали нормой при обучении нейронных сетей, на практике было замечено, что в некоторых случаях, например, для распознавания объектов [17] или машинного перевода [18] эти методы не сходятся к оптимальному решению и их опережает SGD с импульсом. Reddi et al. (2018) [19] формализуют эту проблему и указывают экспоненциальное скользящее среднее (exponential moving average) последних квадратов градиентов как причину плохого обобщающего поведения методов адаптивной скорости обучения. Напомним, что введение экспоненциального среднего было хорошо мотивировано: оно должно предотвратить бесконечно малые скорости обучения в процессе обучения, что является ключевым недостатком алгоритма Adagrad. Однако это кратковременное запоминание градиентов становится препятствием в других сценариях. В условиях, когда Ada m сходится к неоптимальному решению, было замечено, что некоторые мини-пакеты предоставляют большие и информативные градиенты, но, поскольку эт и мини-пакеты встречаются редко, экспоненциальное среднее уменьшает их влияние, что приводит к плохой сходимости. Авторы приводят пример простой выпуклой задачи оптимизации, где такое же поведение можно наблюдать для Ada m. Чтобы исправить это поведение, авторы предлагают новый алгоритм AMSGrad, который использует максимум прошлых квадратов градиентов v t, а не экспоненциальное среднее для обновления параметров. v t определяется так же, как в Ada m: v t = β 2 v t -1 + (1- β 2) gt 2 Вместо v t (или его уточнённой-по-смещению версии
Таким образом, AMSGrad приводит к увеличению размера шага, что позволяет избежать проблем, с которыми сталкивается Ada m. Для простоты авторы также удаляют этап (debiasing) коррекции смещения, присутствующий в Ada m. Полное обновление AMSGrad без исправленных смещений оценок показано ниже:
Авторы наблюдают улучшение производительности по сравнению с Ada m на небольших наборах данных и на CIFAR-10. Другие эксперименты, однако, показывают аналогичную или худшую производительность, чем Ada m. Ещё неизвестно, сможет ли AMSGrad последовательно превзойти Ada m на практике. Для получения дополнительной информации о последних достижениях в области оптимизации Deep Learning см. этот блог.
Визуализация алгоритмов Следующие 2 анимации (рис 5,6. предоставлены: Alec Radford) обеспечивают некоторые интуитивные предположения о поведении оптимизации большинства представленных методов. Также посмотрите здесь описание тех же изображений, сделанных Karpathy, другой краткий обзор обсуждаемых алгоритмов. На Рис.5 видно их поведение на контурах поверхности потерь (Beale function) с течением времени. Обратите внимание, что Adagrad, Adadelta и RMSprop почти сразу же движутся в правильном направлении и сходятся быстро, в то время как импульс и NAG выводятся из «колеи», изображая шар, катящийся вниз по склону. NAG, однако, быстро может скорректировать свой курс благодаря повышенной чувствительности, заглядывая в будущее при движении к минимуму. http://ruder.io/content/images/2016/09/contours_evaluation_optimizers.gif Рис.5: Оптимизация SGD на контурах поверхности потерь http://ruder.io/content/images/2016/09/saddle_point_evaluation_optimizers.gif Рис.6: Оптимизация SGD в седловой точке
На Рис.6 показано поведение алгоритмов в седловой точке, т.е. в точке, где одно измерение имеет положительный наклон, а другое измерение имеет отрицательный наклон, что создает трудности для SGD, как упоминали ранее. Отметьте, что SGD, импульс и NAG испытывают трудности с нарушением симметрии, хотя 2м последним в конечном итоге удаётся избежать седловой точки, в то время как Adagrad, RMSprop и Adadelta быстро снижают отрицательный уклон. Как можно видеть, методы адаптивной скорости обучения, т.е. Adagrad, Adadelta, RMSprop и Adam, являются наиболее подходящими и обеспечивают наилучшую сходимость для этих сценариев. Примечание: если Вы заинтересованы в визуализации этих или других алгоритмов оптимизации, обратитесь к этому полезному руководству.
Hogwild Niu et al. [20] представили схему обновления под названием Hogwild (экстремально увлечённый/вышедший из-под контроля), которая позволяет выполнять обновления SGD на процессорах параллельно. Процессорам разрешен доступ к общей памяти без блокировки параметров. Это работает только в том случае, если входные данные разряжённые, т.к. каждое обновление будет изменять только часть параметров. Авторы показывают, что в этом случае схема обновления достигает почти оптимальной скорости сходимости, поскольку маловероятно, что процессоры будут перезаписывать полезную информацию.
Downpour SGD D ownpour SGD (ливень/поток) – это асинхронный вариант SGD, который использован Dean et al. [10:1] в структуре DistBelief (предшественник TensorFlow) в Google. Он запускает несколько копий модели параллельно на подмножествах обучающих данных. Эти модели отправляют свои обновления на сервер параметров, который распределён по многим машинам. Каждая машина отвечает за хранение и обновление части параметров модели. Однако, поскольку реплики не связываются друг с другом, например, при совместном использовании весов или обновлений их параметры постоянно подвергаются риску расхождения, что препятствует сходимости.
TensorFlow TensorFlow [22] – среда Google (недавно открыт её код) для реализации и развёртывания крупномасштабных моделей машинного обучения. Он основан на их опыте работы с DistBelief и уже используется внутри компании для выполнения вычислений на большом количестве мобильных устройств, а также в крупно распределённых системах. Для распределённого выполнения граф вычислений разбивается на подграф для каждого устройства, а связь осуществляется с использованием пар узлов отправки / получения.
Эластичное усреднение SGD Zhang et al. [23] предлагают SGD для эластичного усреднения (EASGD) (Elastic Averaging), который связывает параметры исполнителей асинхронного SGD с силой упругости (elastic force), т.е. центральной переменной, хранящейся на сервере параметров. Это позволяет локальным переменным колебаться дальше от центральной переменной, что в теории позволяет больше исследовать пространство параметров. Они эмпирически показывают, что эта увеличенная способность к разведке ведет к улучшению производительности путём поиска новых локальных оптимумов. Пакетная нормализация Чтобы облегчить обучение, обычно нормализуем начальные значения параметров, инициализируя так, чтобы их среднее было ноль (zero mean), а дисперсиея – единицей (unit variance). По мере продвижения обучения и обновления параметров в разной степени эта нормализация теряется, замедляя обучение и усиливая изменения по мере глубины сети. Пакетная нормализация (batch normalization) [27] восстанавливает эти нормализации для каждой мини-партии, а изменения также через эту операцию обратно-распространяются (back-propagated) по сети. Делая нормализацию частью архитектуры модели, можно использовать более высокие скорости обучения и уделять меньше внимания параметрам инициализации. Пакетная нормализация дополнительно действует как регуляризатор, уменьшая (а иногда даже устраняя) необходимость в (выбывших) Dropout (метод регуляризации ИНС для предотвращения переобучения сети. Суть метода: в процессе обучения выбирается слой, из которого случайным образом выбрасывается некоторое число нейронов (например, 30%), выключаются из дальнейших вычислений. Такой приём улучшает эффективность обучения и качество результата. Более обученные нейроны получают в сети больший вес).
Ранняя остановка По словам Geoff Hinton: «Ранняя остановка – прекрасный бесплатный обед» (слайд 63, NIPS 2015). Нужно всегда отслеживать ошибки в проверочном наборе (validation set) во время обучения и останавливаться (с некоторым терпением), если проверочная ошибка (validation error) улучшается недостаточно.
Градиент шума Neelakantan et al. [28] добавили шум, который следует распределению Гаусса N(0,σ t 2) для каждого обновления градиента: gt , i = gt , i + N(0,σ t 2) Авторы согласно следующему распределению отжига выбирают дисперсию: σ t 2 = η / (1+t)γ Было показано, что добавление шума делает нейросети более устойчивыми к плохой инициализации и помогает обучать особенно глубокие и сложные сети. Выдвинута гипотеза, что добавленный шум даёт модели больше шансов обеспечить выход и найти новые локальные минимумы, которые характерны более глубоким моделям. Заключение В данной статье были рассмотрены 3 варианта градиентного спуска, среди которых мини-пакетный градиентный спуск является наиболее популярным. Затем были исследованы алгоритмы, которые наиболее часто используются при оптимизации: SGD, Импульс, ускоренный градиент Нестерова, Adagrad, Adadelta, RMSprop, Adam, а также различные алгоритмы для оптимизации асинхронной SGD. Наконец, рассмотрели другие стратегии улучшения SGD, такие как перемешивание и учебныйпланобучения, пакетнаянормализация и ранняяостановка. Надеемся, что статья смогла дать Вам некоторое интуитивное представление в отношении мотивации и поведения различных алгоритмов опт
|
|||||||||||||
|
Последнее изменение этой страницы: 2019-11-02; просмотров: 211; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.105.152 (0.015 с.) |














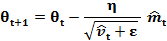
 на ut, чтобы получить правило обновления AdaMax:
на ut, чтобы получить правило обновления AdaMax:





 не нужно):
не нужно):
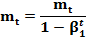

 и mt даёт:
и mt даёт:

 :
:








